机器学习数学系列（3）：概率论选讲

目录：

积分学

　　理解积分：无穷求和，体积

　　微积分基本定理：牛顿-莱布尼兹公式

概率空间

　　随机变量与概率：概率密度函数的积分

　　条件概率

　　共轭分布

大数定律和中心极限定理

　　随机变量的矩

　　切比雪夫不等式

　　大数定律

　　中心极限定理

 

数学记号说明：

 

1 理解积分：无穷求和，体积

1.1 单变量函数黎曼积分

 

理解积分：

　　代数意义：无穷求和

　　几何意义：函数与X轴之间的有向面积　　

2 微积分基本定理：牛顿-莱布尼兹公式

牛顿-莱布尼兹公式展示了微分与积分的基本关系：在一定程度上微分与积分互为逆运算。

例1：

例2：

2.1 多变量积分

多变量函数的积分：

2.2 小结（积分学）

积分的代数意义是无穷求和，几何意义是带符号的体积。

微分和积分在一定程度上互为逆运算。

熟悉微分公式有助于计算积分。

多重积分可以理解成是依次进行的单重积分。

3 随机变量与概率：概率密度函数的积分

3.1 离散随机变量

对于离散随机变量，概率为概率函数的求和。

3.2 连续随机变量

3.3 如何理解概率

3.3.1 事件的概率

3.3.2 事件的条件概率

概率其实就是集合的大小比例，而概率函数或者概率密度函数可以理解为比较大小时候的权重。

3.4 贝叶斯公式

3.4 共轭分布

 

 

3.5 先验分布，似然函数，后验分布

3.6 小结（随机变量与概率）

概率可以理解为事件所代表的集合在全概率空间中的比例。

对于概率分布参数的先验分布有不同的观点。

如果参数先验分布与后验分布属于同一类，则叫做共轭分布。

4 大数定律和中心极限定理

4.1 随机变量的矩：

4.2 切比雪夫不等式

4.3 随机变量的相关系数

4.4 独立随机变量

4.5 利用特征函数研究概率分布

刚才介绍了同一随机变量的特征函数的重要性质 ，下面列举一些不同随机变量的特征函数的重要性质。

4.6 特殊分布的特征函数

4.7 复习一个重要极限

自然对数底数e的定义：

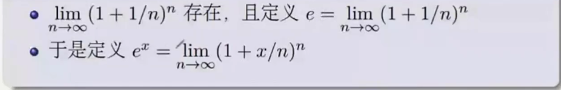
4.8 大数定律

证明：

按分布收敛于独点分布就等于按概率收敛于一个常数。

4.9 中心极限定理

证明：

4.10 小结（切比雪夫不等式，大数定律，中心极限定理）

随机变量的矩可以描述随机变量所服从的性质。

随机变量的特征函数可以全面描述随机变量的分布

切比雪夫不等式指出方差可以描述随机变量取值的分散程度。

大数定律指出独立重复实验的平均值的收敛规律。

中心极限定理给出独立重复实验平均值更细致的描述。