机器学习数学系列(2):微分选讲
主要内容:
极限:
复习极限记号,无穷大无穷小阶数
微分学(尚不讲积分):
复习函数求导,泰勒级数逼近
牛顿法与梯度下降法
Jensen不等式
复习凸函数,Jensen不等式的证明
一些记号说明:

1 极限

通俗语言适合说给对方听,数学记号适合写给对方看,精确描述比较啰嗦但是非常精确不会造成误解,主要用于证明。
1.1 极限:如何比较无穷小
无穷也分大小,如何描述与比较无穷大和无穷小

我们考察这两个函数的商的极限
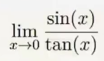 =1
=1

1.2 极限:无穷小阶数

所谓无穷小的阶数,就是用我们比较熟悉的多项式类型的无穷小量来衡量其他的无穷小量,把未解决的问题转化为已经解决的问题,这是数学家的“惯用伎俩”。


注:提醒一下,对于第一个极限,不能使用洛必达法则,可以使用夹逼定理来证明,你可有记起?
1.3 小结
极限有不同的表述方式,建议练习使用 语言。
语言。
无穷小也可以互相比较。
利用多项式类型无穷小,可以定义无穷小的阶数。
夹逼原理。
2 微分学
微分学的核心思想:逼近
2.1 函数导数的定义

等价定义:
无穷小量表述:线性逼近

函数的高阶导数的定义:

导数是对函数进行线性逼近,高阶导数是对导数函数的进一步逼近,因为没有更好的办法,所以数学家选择继续使用线性逼近。
初等函数的导数:

2.2 多元函数
我们在此只考虑无穷次可微的多元函数,对于这种函数我们可以使用全微分来定义偏导数,实际上现实遇到的函数大部分都是这种函数。
全微分与偏导数:

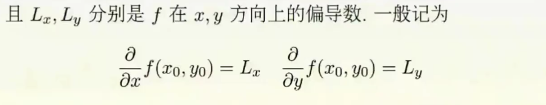
高阶偏导数:

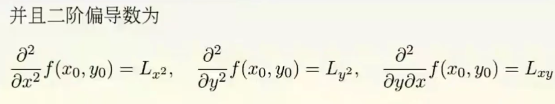
偏导数的例子:

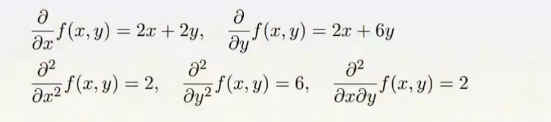
求导法则:

所有求导法则原则上都可以由链式法则结合二元函数的偏导数来推出来,有兴趣可以思考一下为什么?
例子:

2.3 小结
微分学的核心思想是逼近
一阶导数:线性逼近
二阶导数:二次逼近
导数计算:求导法则
3 一元微分学的顶峰:泰勒级数
用多项式逼近的方式描述高阶导数,我们就得到了泰勒级数
3.1 泰勒/麦克劳林级数:多项式逼近

最后一项为余项。
泰勒级数的一些例子:
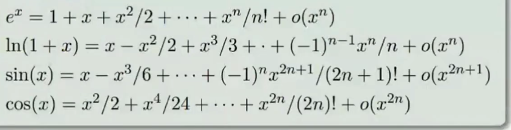
插播一条:史上最美的数学公式---欧拉公式
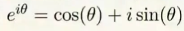
3.2 用泰勒级数来理解问题
泰勒级数是一元微分逼近的顶峰,所以有关于一元微分逼近的问题请尽情使用。
3.2.1 洛必达法则:
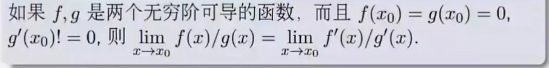

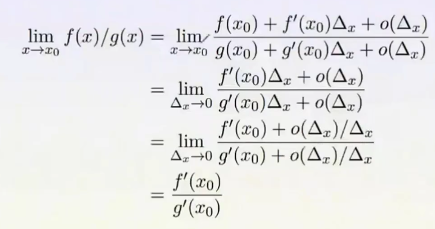
3.2.2 求解简单的微分方程


3.3 小结(泰勒级数)
泰勒级数本质是多项式逼近。
特殊函数的泰勒级数可以适当记一下。
泰勒级数可以应用于很多与逼近相关的问题。
4 牛顿法与梯下降法
很多机器学习或者统计的算法最后都转化成一个优化问题,也就是求某一个损失函数的极小值问题,下面我们先只考虑可微分的函数极小值问题。
优化问题:

极值点条件:

4.1 局部极值算法
我们利用极值点条件,来介绍牛顿法和梯度下降法
这两种方法都只能寻找局部极值。
这两种算法都要求必须给出一个初始点x0。
数学原理:牛顿法使用二阶逼近,梯度下降法使用一阶逼近。
牛顿法对局部凸的函数找到极小值,对局部凹的函数找到极大值,对局部不凸不凹的可能会找到鞍点。
梯度下降法一般不会找到最大值,但是同样可能会找到鞍点。
当初始值选取合理的情况下,牛顿法比梯度下降法收敛速度快。
牛顿法要求估计二阶导数,计算难度更大。
4.2 牛顿法:一元函数二次逼近

4.3 牛顿法:多变量函数二次逼近

4.4 梯度下降法:多变量函数一阶逼近

4.5 小结(牛顿法与梯度下降法)
牛顿法与梯度下降法本质上都是对目标函数进行局部逼近。
因为是局部逼近所以也只能寻找局部极值。
牛顿法收敛步骤比较少,但是梯度下降法每一步计算更加简单。
不同的算法之间很难说哪一个更好,选择算法还要具体问题具体分析(这也是数据科学家存在的意义之一)
5 凸函数与琴生不等式
对于凸优化来说,局部极值与整体极值没有区别,这个比较简单,所以从这个开始研究。
当不知道做什么的时候,选择最简单的问题开始做起,这也是数学家的惯用“伎俩”。
5.1 凸函数定义

5.2 凸函数的判断准则
一个二阶可微的函数f是凸函数,当且仅当f ''(x)>=0,x取任意值。

5.3 凸函数重要性质:琴生不等式






