论文笔记(9):Multiscale Combinatorial Grouping
本文大致脉络:
对每张图片,作者首先使用 P. Doll´ar and C. Zitnick. Structured forests for fast edge detection. ICCV , 2013. 4, 5 来产生边缘图(edge probability map),请注意probability,因为下面connected regions 之间的 similarity 就是通过 这个probability 来体现的, 这里的probability 指的是该点的像素属于边缘的概率。对边缘图进行watershed得到轮廓图,通过对轮廓图进行一系列操作得到UCM图,如下图:
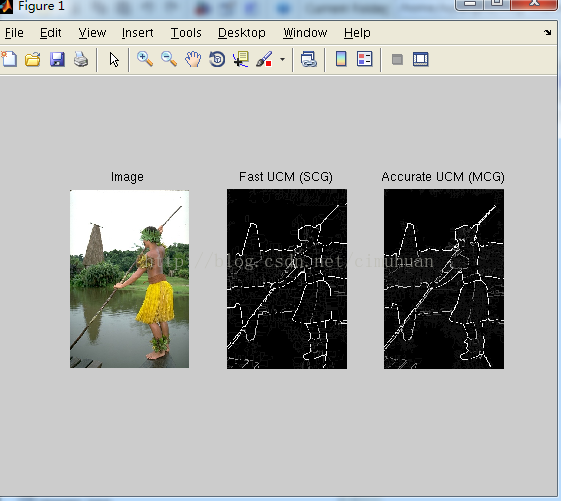
在UCM图里,黑色区域部分可以认为是connected regions,该图通过白色部分分离开来,白色部分的每个像素都是一个实值(0-1),图中每条边的一小段的像素值都是相同的,该值表示该边所连接区域的不相似度,值越小,这两个区域越有可能合并称为一个区域。利用UCM图,获取图像的superpixels,也就是一个个connected regions ,任意两个相邻的 regions 之间都有一个不相似度值。
接下来就是要对这所有的N个regions hierarchically 合并了, 方法就是将N个叶子节点两两合并,最终得到 N-1个非叶子节点,这样就构造了一颗完全二叉树,二叉树的根部是整个图像区域,叶子节点就是一开始得到的 superpixels。这样一张UCM图可以得到一个 hierarchical segmentation。这里的初始的superpixels和组合后的非叶子节点都可以看做是一个proposals,这样一共是2N-1个proposals。
得到该树后,作者从二叉树离获取 4个list 的proposals。分别是 singleton, pairs, triplets ,fours。在获取的时候使用了Pareto optimization,看着挺高深,其实就是 4个整数值,我们以这样的一个组合为例(700,2000,3000,2000)。700对应于 singleton,表示从 二叉树中从顶向下取前700个proposals。对于二叉树的非根节点来说,每个节点都有父母,每个父母都有自己的兄弟,那么每个节点都有一个叔叔,pairs就表示叔叔与侄子的组合,比如说4个节点 1、2、3、4,1和2 组成了5,3和4组成了6,那么5就是1和2 的父节点,6是3和4的父节点,5是3和4的叔叔,那么在pairs里5、3可以是一种组合,一种新的proposals,2000表示从这所有的叔叔-侄子组合中,自顶向下去2000个这样的组着,那么triplets中的3000就表示 侄子-叔叔-叔叔的叔叔的3000中组合,同理fours. 这样对每张UCM图,会到一个一个bottom-up组合,然后从该组合中可以得到4个list的proposals。
在作者的代码中实际上是对原来的图片进行scale (2,1,0.5),这样一共可以得到3张UCM图,然后将三张UCM图融合,这样一共有 四种UCM图,每种UCM都可以得到4个list的proposals,一共有16个lists的proposals,作者收集zhexieproposals,然后对他们进行 overlap>0.95的筛选。然后再进行hole-filling,因为在之前的组合中可能某种proposals会有明显的hole inside。
最后,在得到一个完整的proposals set后,作者提取每个proposals 的 面积、周长、边界强度等2D基本特征,用这些特征组成向量来表示该proposal,然后训练随机森林回归器来对这些proposals排名。
作者提供了两个版本的UCM,Fast UCM 和Accurate UCM正如图所示, Fast UCM 最终会得到4个list的proposals, Accurate 会得到16个list的 proposals。
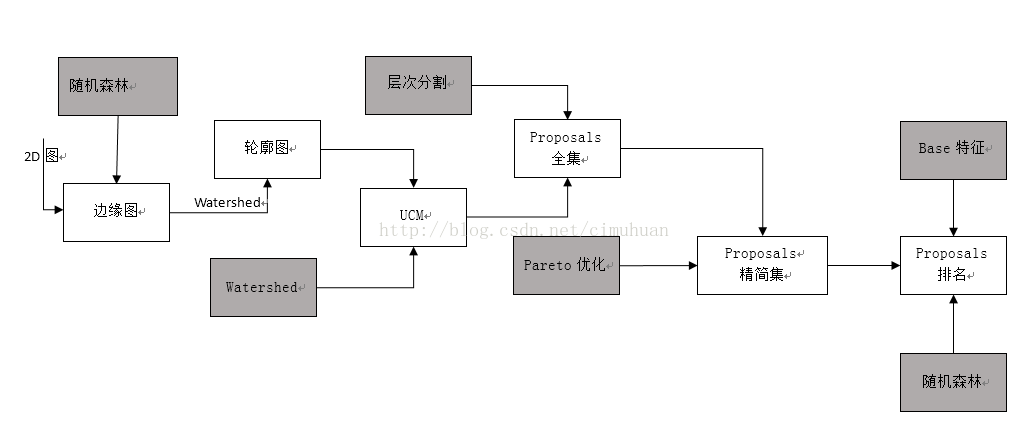
最后附上MCG简易流程图: