【二叉搜索树】LeetCode 96. 不同的二叉搜索树【中等】

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

 

 

 

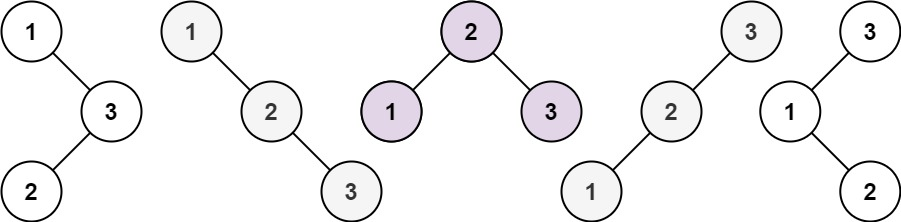
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1 

提示：

• 1 <= n <= 19

【分析】

方法一：动态规划

给定一个有序序列"1...n", 为了构建出一棵二叉搜索树，我们可以遍历每个数字i，将该数字作为树根，将1...(i-1)作为左子树，将(i+1)...n作为右子树。接着我们可以按照同样的方式递归构建左子树和右子树。

在上述构建的过程中，由于根的值不同，因此我们能保证每一棵二叉搜索树为唯一的。

由此可见，原问题可以分解成两个规模较小的子问题，且子问题的解可以复用。因此，我们可以想到使用动态规划来求解本题。

算法：

题目要求是计算不同二叉搜索树的个数。为此，我们可以定义两个函数：

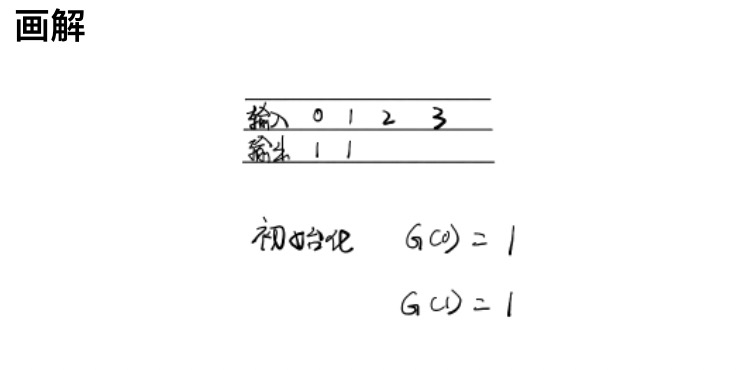
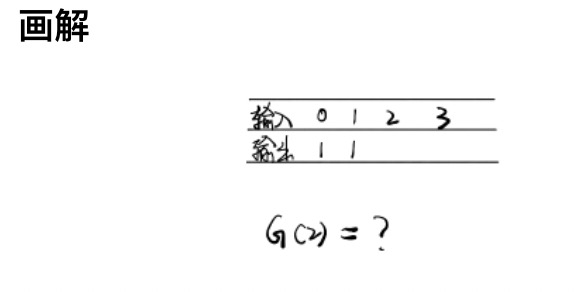
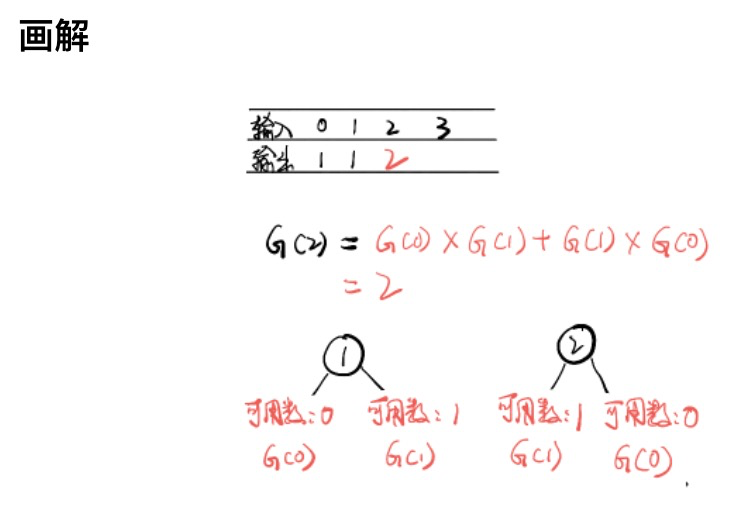
假设n个节点存在二叉排序树的个数是G(n)，令f(i)为以i为根的二叉搜索树的个数，则：

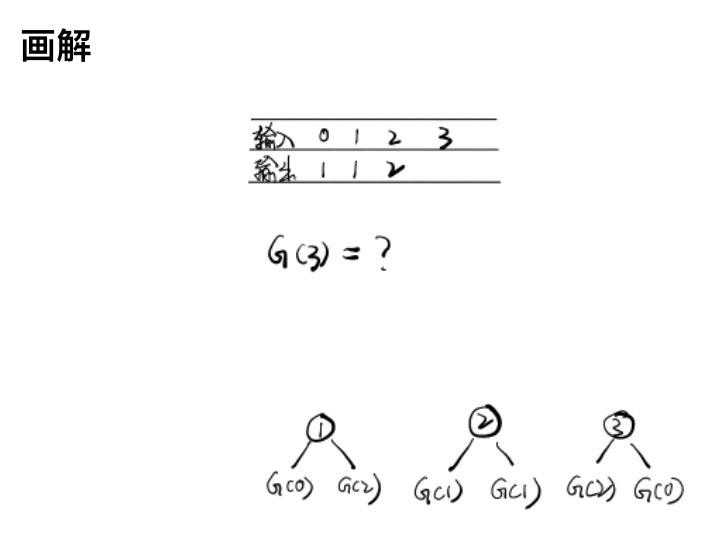
G(n) = f(1) + f(2) + ... + f(n)

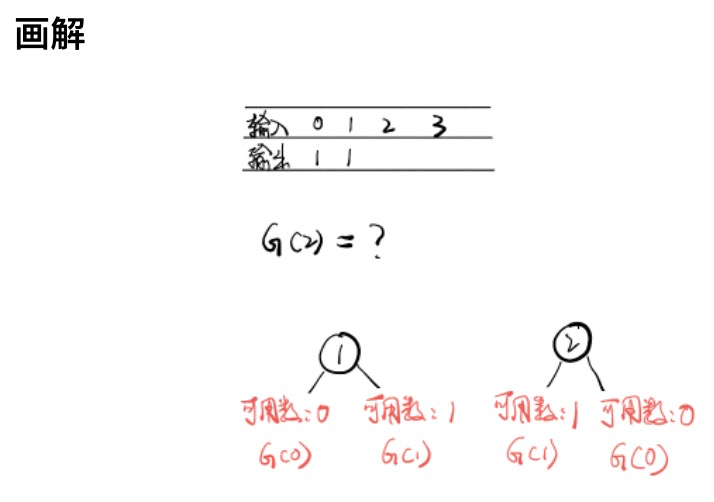
那么，当i为根节点时，其左子树节点个数为i - 1个，右子树节点个数n - i个，则：

f(i) = G(i - 1) * G(n - i)

综合以上两个公式可以得到卡特兰数公式（https://baike.baidu.com/item/%E5%8D%A1%E7%89%B9%E5%85%B0%E6%95%B0）：

G(n)  = f(1) + f(2) + ... + f(n) 

        = G(0)*G(n-1) + G(1)*G(n-2) + ... + G(n-1)*G(0)

class Solution:
    def numTrees(self, n: int) -> int:
        dp = [0]*(n+1) # 这里的dp相当于卡特兰数的变量G
        dp[0], dp[1] = 1, 1

        for i in range(2, n+1):
            for j in range(1, n+1):
                dp[i] += dp[j-1] * dp[i-j]
        return dp[n] 

这里有详细分析：

https://leetcode.cn/problems/unique-binary-search-trees/solution/bu-tong-de-er-cha-sou-suo-shu-by-leetcode-solution/

时间复杂度：O(n²)，其中n表示二叉搜索树的节点个数。dp(n)函数一共有n个值需要求解，每一次求解需要O(n)的时间复杂度，因此总时间复杂度为O(n²)。

空间复杂度：O(n)。我们需要O(n)的空间存储dp数组。

方法二：数学

事实上，我们在方法一中推导出的dp(n)函数的值在数学上被称为卡特兰数C_n。卡特兰数更便于计算的定义如下：

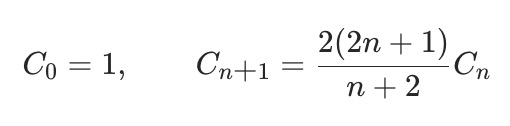
class Solution:
    def numTrees(self, n: int) -> int:
        C = 1
        for i in range(n):
            C = C * 2*(2*i+1) / (i+2)
        return int(C) 

时间复杂度：O(n)，其中n表示二叉搜索树的节点个数。我们只需要循环遍历一次即可。

空间复杂度：O(1)，我们只需要常数空间存放若干变量。