【二叉树】106. 从中序与后序遍历序列构造二叉树 【中等】

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这棵 二叉树 。

示例1:

 

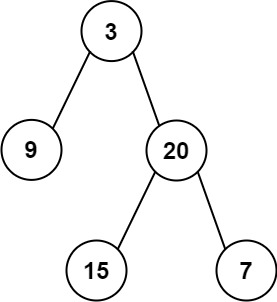
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]
示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]
 

提示:

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由 不同 的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历

 

【分析】

一句话题解：

二叉树后续遍历的最后一个元素一定是根节点；

二叉树的根节点把中序遍历序列分成两个区间：

　　左边区间的所有节点构成根节点的左子树；

　　右边区间的所有节点构成根节点的右子树。

递归构建二叉树即可。

思路分析：

解决二叉树的问题通常会用到分治思想，分治思想一般通过递归方法实现。

复习一下分治法的思想：把原问题分解成若干个于原问题结构相同当规模更小的子问题，待子问题解决以后，再合并它们，原问题就得以解决。

归并排序和快速排序是典型的分治思想的应用，其中：

　　归并排序先无脑“分”，在“合”的时候就嘛烦一些；

　　快速排序在“分”上花了很多时间，然后就递归处理下去就好了，没有在“合”的过程。

以题目中给出的例子为例，讲解如何构建二叉树。

中序遍历inorder = [9，3，15，20，7]

后序遍历postorder = [9，15，7，20，3]

 

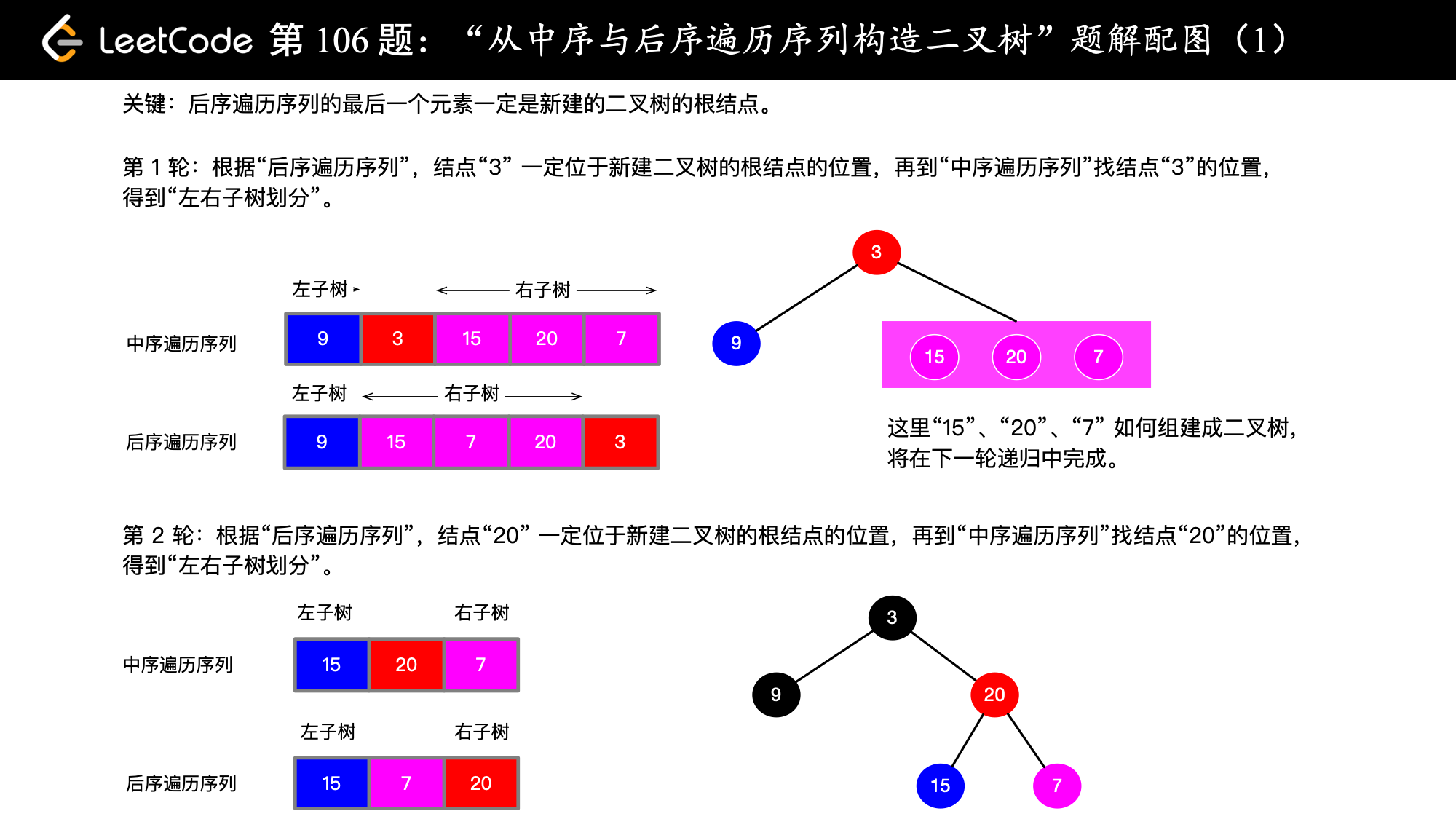
 注意：这道题并不难，在草稿纸上写写画画，就能把思路想清楚，但是在编码上会有一些小陷阱，在计算索引边界值的时候要仔细一些。

下面给我两种写法，区别在于空间复杂度：

方法一：在递归方法中，传入数组的拷贝（不推荐，复杂度高）

该方法在计算索引的时候会稍微容易一些。

from typing import List


class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        assert len(inorder) == len(postorder)

        if len(inorder) == 0:
            return None
        if len(inorder) == 1:
            # 这里要返回结点，而不是返回具体的数
            return TreeNode(inorder[0])
        # 后序遍历的最后一个结点就是根结点
        root = TreeNode(postorder[-1])
        # 在中序遍历中找到根结点的索引，得到左右子树的一个划分
        pos = inorder.index(postorder[-1])
        # 这里的列表切片使用的是复制值，使用了一些空间，因此空间复杂度是 O(N)
        root.left = self.buildTree(inorder[:pos], postorder[:pos])
        root.right = self.buildTree(inorder[pos + 1:], postorder[pos:-1])
        return root

复杂度分析：时间复杂度：O(N²), 这里 N 是二叉树的结点个数，算法中每个结点都会被看到一次，而查找根结点在中序遍历序列中的位置，又需要遍历一次，递归的深度是对数级别的，因此时间复杂度是O(N²)。

空间复杂度：O(N)，构造一棵树需要 N 个结点。

 

方法二：在递归方法中，传入子数组的边界下标。

注意：在递归方法中，有一个数组的边界下标。

计算的依据是递归方法传入的中序遍历数组（的子数组）和后序遍历遍历数组（的子数组）的长度相等。这里采用的办法是解方程计算未知数，具体需要计算哪个参数在下面代码中已经注明了。

下面展示了一个计算边界的方法：

 

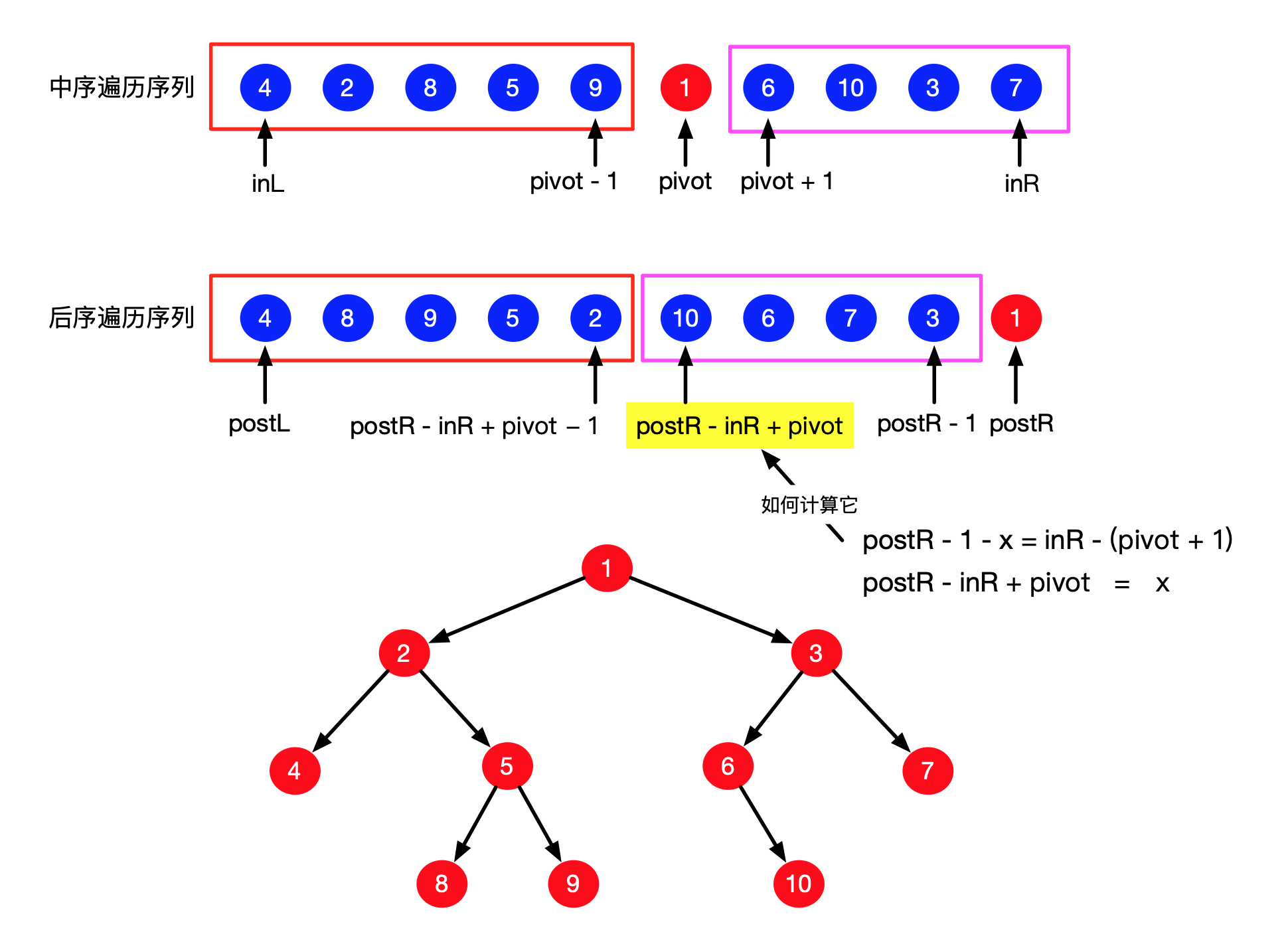
这样，可以在递归构造前，把中序遍历的值和下标放在哈希表中，就不需要通过遍历得到当前根结点在中序遍历中的位置了。

from typing import List


class Solution:

    def __init__(self):
        self.inorder = None
        self.postorder = None

    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        assert len(inorder) == len(postorder)
        size = len(inorder)

        self.inorder = inorder
        self.postorder = postorder
        return self.__dfs(0, size - 1, 0, size - 1)

    def __dfs(self, in_l, in_r, post_l, post_r):
        if in_l > in_r or post_l > post_r:
            return None

        val = self.postorder[post_r]
        # 后序遍历的最后一个结点就是根结点
        root = TreeNode(val)
        # 在中序遍历中找到根结点的索引，得到左右子树的一个划分
        pos = self.inorder.index(val)

        # 注意：第 4 个参数是计算出来的，依据：两边区间长度相等
        root.left = self.__dfs(in_l, pos - 1, post_l, pos - 1 - in_l + post_l)
        # 注意：第 3 个参数是计算出来的，依据：两边区间长度相等
        root.right = self.__dfs(pos + 1, in_r, post_r - in_r + pos, post_r - 1)
        return root