【二叉树】LeetCode 104. 二叉树的最大深度【简单】
给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例：
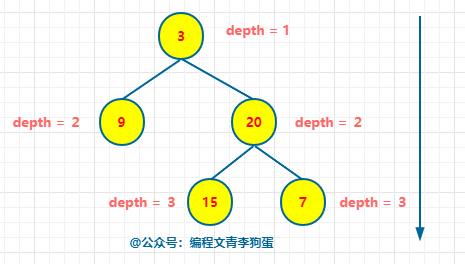
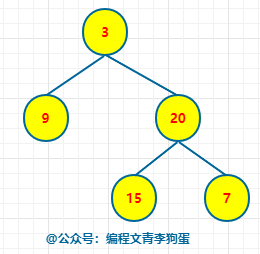
给定二叉树 [3,9,20,null,null,15,7]，
3 / \ 9 20 / \ 15 7
返回它的最大深度 3 。
【分析】
方法一：深度优先搜索
如果我们知道了左子树和右子树的最大深度l和r，那么该二叉树的最大深度即为：max(l, r) + 1
而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用“深度优先搜索”的方法来计算二叉树的最大深度。
具体而言，在计算当前二叉树的最大深度时，可以先递归计算出其左子树和右子树的最大深度，然后在O(1)时间内计算出当前二叉树的最大深度，递归操作在访问到空节点时退出。
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def maxDepth(self, root: Optional[TreeNode]) -> int: if not root: return 0 else: left_h = self.maxDepth(root.left) right_h = self.maxDepth(root.right) return max(left_h, right_h) + 1 # 时间复杂度：O(n)，其中 n 为二叉树节点的个数。每个节点在递归中只被遍历一次。 # 空间复杂度：O(height)，其中 height 表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度。
【细说一些】：
解决这道题的重点，其实是考察你对二叉树的概念是否到位。
懂了概念，这道题的解法也就出来了，而且是不止一个的解法。
这道题是求二叉树的最大深度，二叉树的深度是从根节点开始算起，依次往下是深度1、2、...
可以理解成一口井，从上往下看，也就是自顶向下看。
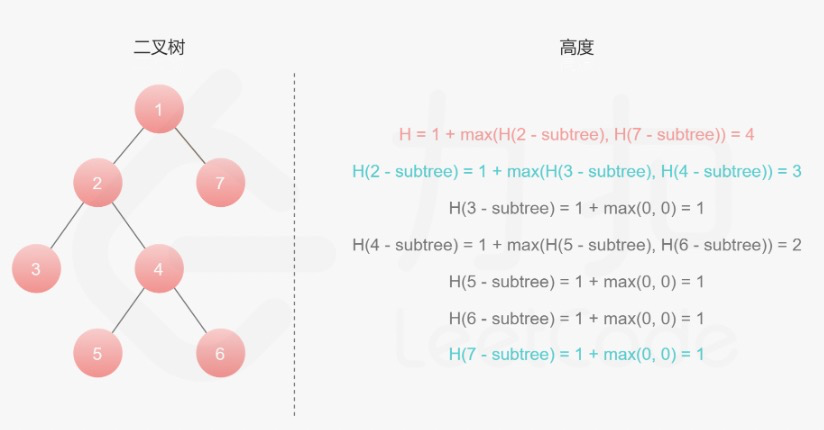
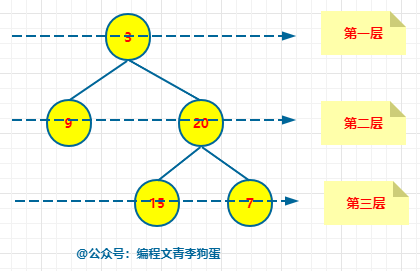
我们来看下面这张图：
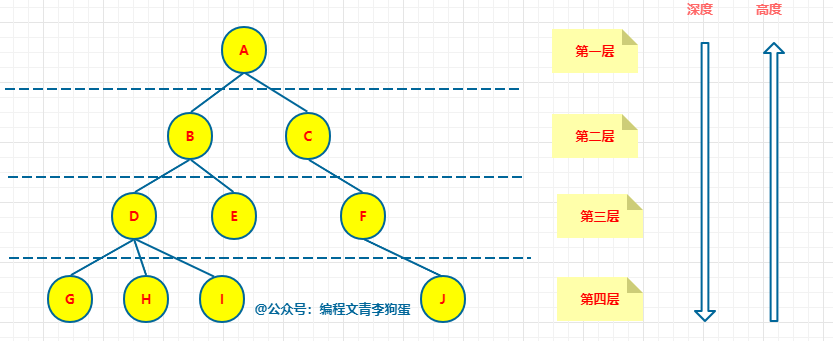
这张图中，有三个树的重要概念：层次、深度、高度。
二叉树的层次是从根节点算起，根节点是第一层，依次往下类推。
二叉树的高度是从叶子节点算起，叶子节点高度是1，依次往上类推。可以看成是高楼，从地面往上看，也就是自底向上看。
通过图片可以看出，二叉树的深度和层次是完全对应的，最大深度为最大层次数，二叉树的深度和高度是正好相反。
了解了这些，你会发现根据看的顺序不同，这道题的三种常规解法：
（1）自顶向下
自顶向下，就是从根节点递归到叶子节点，计算这一条路径上的深度，并更新维护最大深度。
这个是正而八经的求深度。每次先维护根节点的深度，再递归左子树，右子树。
每次都是先根节点，再是左子树，最后右子树，说白了用的其实就是前序遍历的方式。
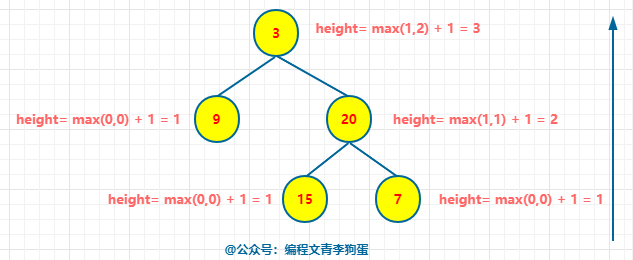
（2）自底向上
从叶子节点开始，一层一层向上，最终汇集在根节点。
这种求的其实是二叉树的高度。先遍历左子树，找出最大高度，再遍历右子树，找出最大高度，最后在根节点取左子树和右子树高度值大的那个，加上根节点的高度为1，即 max(leftHeight, rightHeight) + 1 为当前二叉树的最大高度。
因为二叉树的最大高度等于最大深度，所以即可同时求出二叉树的最大深度。
可以看出，这种先递归左子树，再递归右子树，最后再根节点，用的其实是后续遍历。
（3）自左向右
自左向右，就是从根节点开始，一层一层地遍历二叉树。
这种求的是二叉树的层次数，二叉树的最大层次就是其最大深度。
可以看出，这种一层一层的遍历，其实用的就是层次遍历。
递归：
递归法，以自底向上，即后续遍历的方式为例，解决本题，这样相对更好理解。
既然是使用递归法，还是按照递归标准，祭出递归二步曲：
（1）找出重复的子问题。
后续遍历的顺序是：左子树、右子树、根。
在本题目中同样也是这个顺序：递归左子树的最大高度，递归右子树的最大高度，求根的最大高度。
对于左子树和右子树来说，也都是同样的操作。
# 递归计算左子树的最大深度 leftHeight = self.maxDepth(root.left) # 递归计算右子树的最大深度 rightHeight = self.maxDepth(root.right) # 二叉树的最大深度 = 子树的最大深度 + 1 （1是根节点那一层） maxHeight = max(leftHeight, rightHeight) + 1
(2) 确定终止条件
对于二叉树来说，没东西遍历了，自然就终止了。
那就是当前节点是空的，既然是空的那就没啥好遍历的了。
# 节点为空，高度为0 if root == None: return 0
这两点确定好了，代码也就出来了。
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def maxDepth(self, root: Optional[TreeNode]) -> int: if not root: return 0 leftHeight = self.maxDepth(root.left) rightHeight = self.maxDepth(root.right) return max(leftHeight, rightHeight) + 1
非递归法（迭代）：
迭代法，以自左向右，即层次遍历的方式为例。
非递归版的层次遍历用的则是队列，这是由于层次遍历的属性非常契合队列的特点。
具体做法是：使用队列保存每一层的所有节点，把队列中的所有节点出队，然后把这些出去的节点各自的子节点入队列。用depth维护每一层。
比如对于下图：
首先初始化队列queue和层次depth，将根节点入队列：
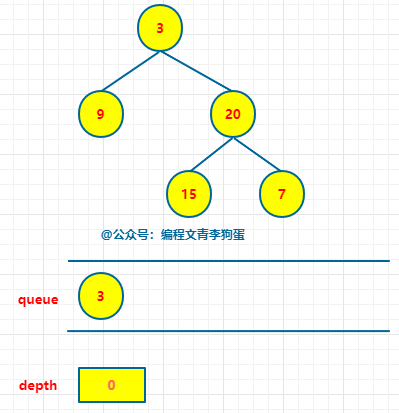
# 初始化队列和层次 queue = [root] depth = 0
当队列不为空，3出队，将其子节点9，20入队列。
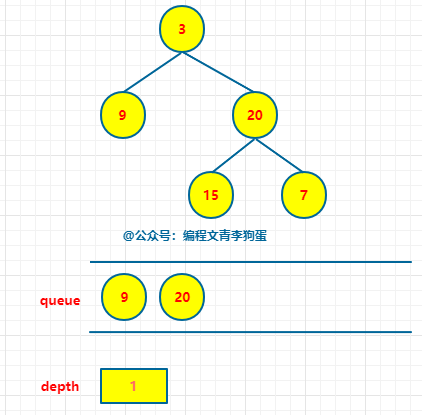
# 当队列不为空 while queue: # 当前层的节点数。 n = len(queue) # 弹出当前层所有节点 for i in range(n): node = queue.pop(0) if node.left: queue.append(node.left) if node.right: queue.append(node.right) depth += 1
下面就是按照上述方式，出队列，入队列，维护当前层，直至队列为空：
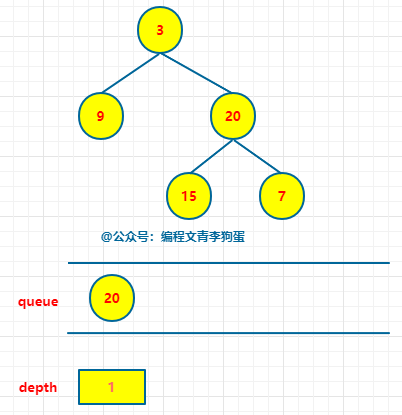
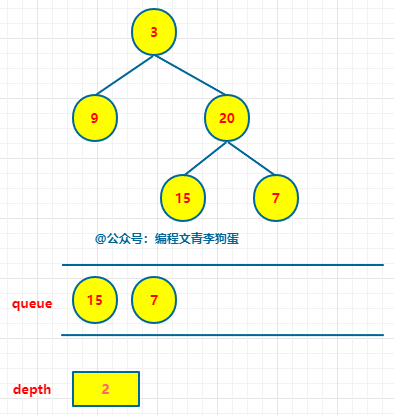
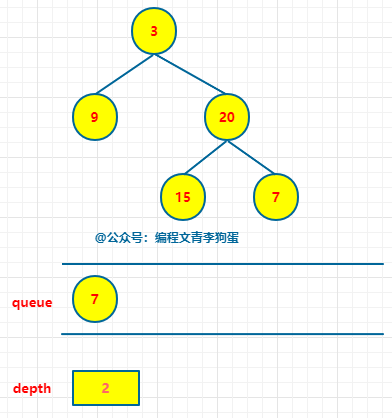
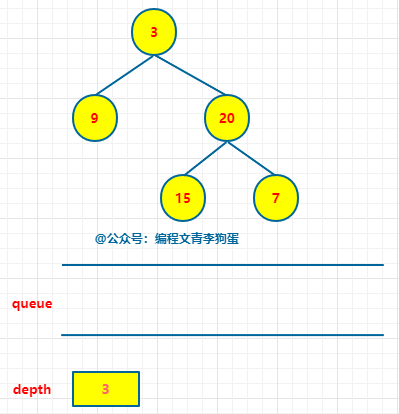
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def maxDepth(self, root: Optional[TreeNode]) -> int: # 空树，高度为 0 if root == None: return 0 # 初始化队列和层次 queue = [root] depth = 0 # 当队列不为空 while queue: # 当前层的节点数 n = len(queue) # 弹出当前层的所有节点，并将所有子节点入队列 for i in range(n): node = queue.pop(0) if node.left: queue.append(node.left) if node.right: queue.append(node.right) depth += 1 # 二叉树最大层次即为二叉树最深深度 return depth # 对于每个节点，各进出队列一次，所以时间复杂度为 O(n)。 # 此外，额外维护了一个队列，所以空间复杂度为 O(n)。
