【哈希表】LeetCode 141. 环形链表【简单】

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false 。

 

示例 1：

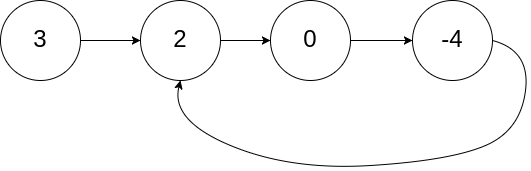
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

 

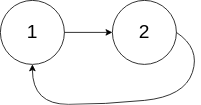
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

 

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。
 

提示：

链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105
pos 为 -1 或者链表中的一个 有效索引 。
 

进阶：你能用 O(1)（即，常量）内存解决此问题吗？

【分析】

方法一：哈希表

最容易想到的方法是遍历所有节点，每次遍历到一个节点时，判断该节点此前是否被访问过。

具体地，我们可以使用哈希表来存储所有已经访问过的节点。每次我们到达一个节点，如果该节点已经存在于哈希表中，则说明该链表是环形链表，否则就将该节点加入哈希表中。重复这一过程，直到我们遍历完整个链表即可。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        seen = set() # 定义一个哈希表
        while head:
            if head in seen: 
                return True
            seen.add(head)
            head = head.next
        return False


# 复杂度分析
# 时间复杂度：O(N)，其中 N 是链表中的节点数。最坏情况下我们需要遍历每个节点一次。
# 空间复杂度：O(N)，其中 N 是链表中的节点数。主要为哈希表的开销，最坏情况下我们需要将每个节点插入到哈希表中一次。

方法二：快慢指针

本方法需要读者对“Floyd判圈算法（又称龟兔赛跑法）”有所了解。

假想乌龟和兔子从链表上的同一个节点开始移动，兔子跑得快，乌龟跑得慢。当乌龟和兔子从链表的同一个节点开始移动时，若该链表中无环，那么兔子将一直处于乌龟的前方；若有环，那么兔子会先于乌龟进入环，并且一直在环内移动。等到乌龟进入环时，由于兔子速度快，它一定会在某个时刻与乌龟相遇。

我们可以根据上述思路来解决本题。具体地，定义两个指针，一块一慢。慢指针每次只移动一步，而快指针每次移动两步。初始时，慢指针位置在head处，而快指针位置在head.next处。这样一来，如果在移动过程中，快指针反过来追上了慢指针，就说明该链表存在环形链表。否则快指针将到达链表尾部，该链表不是环形链表。

 

细节：

为何要规定初始时慢指针在位置head，快指针在位置head.next（即与乌龟和兔子故事中的叙述相同）？

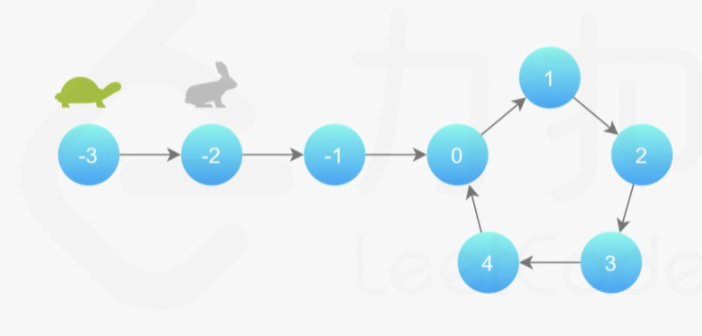
　　观察👀下面代码，我们使用的是while循环，循环条件先于循环体。由于循环条件一定是判断快慢指针是否重合，如果我们将两个指针初始都置于head，那么while循环就不会执行，因为已经已经处于重合状态了。因此，我们可以假想一个在head之前的虚拟节点，慢指针从虚拟节点移动一步到达head，快指针从虚拟节点移动两步到达head.next，这样我们就可以使用while循环了。

　　当然，我们也可以使用do-while循环。此时，我们就可以吧快慢指针初始值都置为head。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        if not head or not head.next:
            return False
        
        slow = head
        fast = head.next
        while slow != fast:
            if not fast or not fast.next:
                return False
            slow = slow.next
            fast = fast.next.next
        
        return True
        


# 复杂度分析
# 时间复杂度：O(N)，其中 N 是链表中的节点数。
# 当链表中不存在环时，快指针将先于慢指针到达链表尾部，链表中每个节点至多被访问两次。
# 当链表中存在环时，每一轮移动后，快慢指针的距离将减小一。而初始距离为环的长度，因此至多移动 N 轮。
# 空间复杂度：O(1)。我们只使用了两个指针的额外空间。