【队列&栈】LeetCode 84. 柱状图中最大的矩形【困难】
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。
示例1:
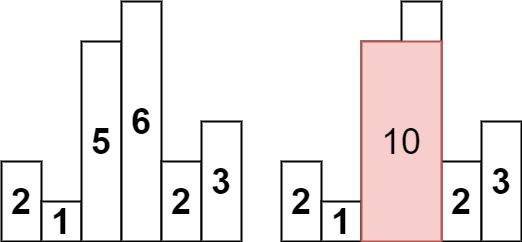
输入：heights = [2,1,5,6,2,3] 输出：10 解释：最大的矩形为图中红色区域，面积为 10
示例 2：
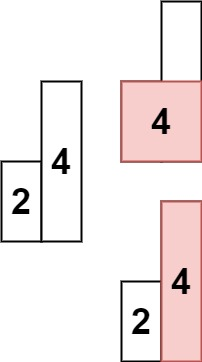
输入： heights = [2,4]
输出： 4
提示：
1 <= heights.length <=105
0 <= heights[i] <= 104
【分析】
方法一：暴力解法
这道题的暴力解法比接雨水那道题要好想得多：可以枚举以每个柱形为高度的最大矩形的面积。
具体来说，依次遍历柱形的高度，对于每一个高度分别向两边扩散，求出以当前高度为矩形的最大宽度是多少。
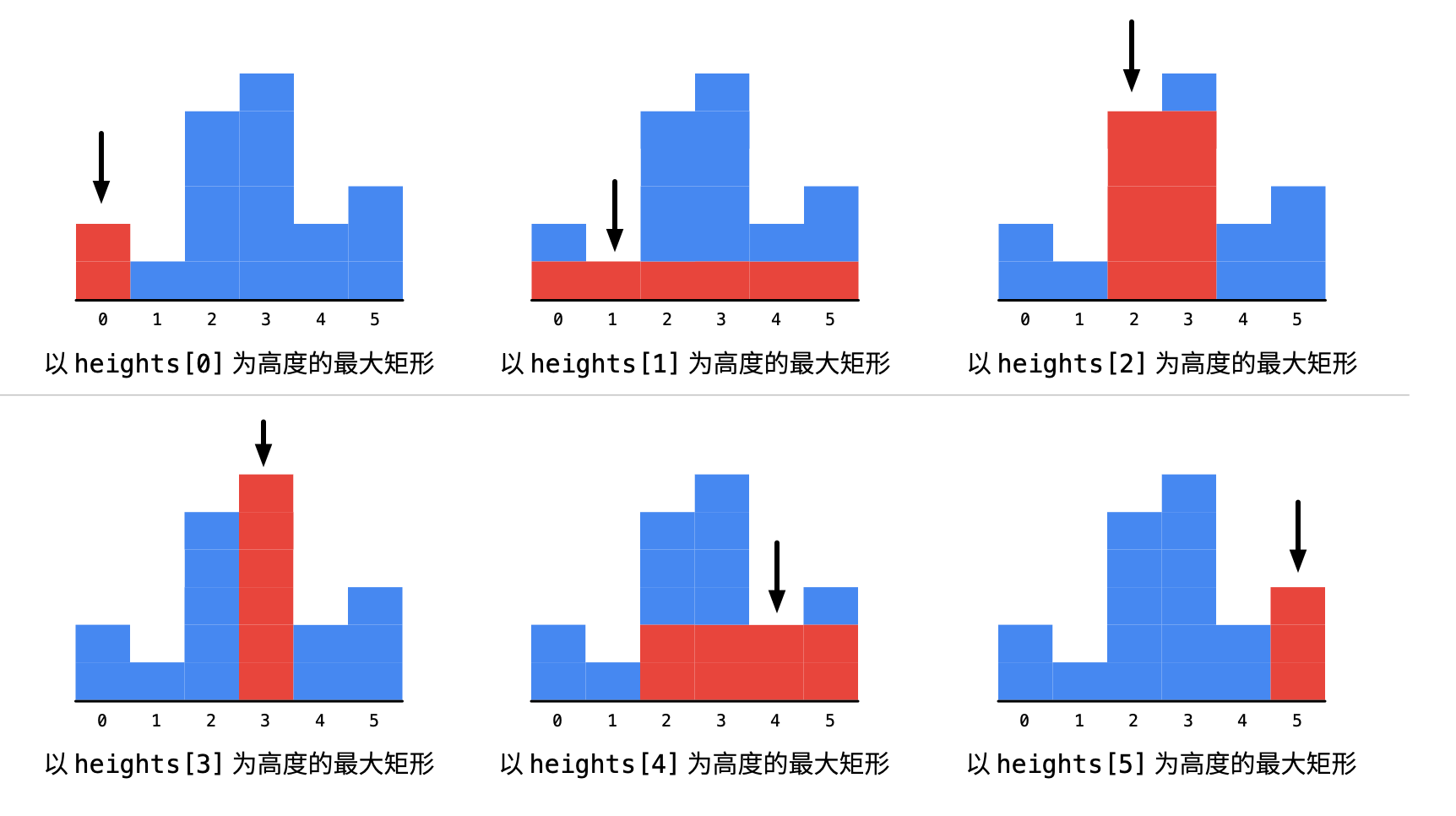
为此，我们需要：
左边看一下，看最多能向左延伸多长，找到大于等于当前柱形高度的最左边元素的下标；
右边看一下，看最多能向右延伸多长；找到大于等于当前柱形高度的最右边元素的下标。
对于每一个位置，我们都这样操作，得到一个矩形面积，求出他们的最大值。
class Solution: def largestRectangleArea(self, heights: List[int]) -> int: size = len(heights) # 柱子数量/数组长度 area = 0 # 初始化矩形面积 for i in range(size): # 遍历 # 1. 先看看左边 left = i # 初始化左指针 cur_height = heights[i] # 左指针所值柱子高度作为当前柱子高度 # 当左指针大于0，且左指针左边相邻柱子高度大于等于当前柱子高度 while left > 0 and heights[left - 1] >= cur_height: left -= 1 # 继续往左边看 # 2. 再看看右边 right = i # 初始化右指针，依然从i开始遍历 # 当右指针大于0，且右指针右边相邻柱子高度大于等于当前柱子高度 while right < size - 1 and heights[right + 1] >= cur_height: right += 1 # 继续往右边看 max_width = right - left + 1 area = max(area, max_width * cur_height) return area
复杂度分析：
- 时间复杂度：O(N2)，这里 N 是输入数组的长度。
- 空间复杂度：O(1)。
看到O(N2)和O(1)的时空复杂度组合，
那么我们是不是可以一次遍历，不需要中心扩散就能够计算出每一个高度所对应的那个最大面积矩形的面积呢？
很容易想到的优化的思路就是「以空间换时间」。我们需要在遍历的过程中记录一些信息。
方法二：以空间换时间，可以使用的数据结构是栈。
要搞清楚这个过程，请大家一定要在纸上画图，搞清楚一些细节，这样在编码的时候就不容易出错了。
记录什么信息呢？记录高度是不是可以呢？其实是不够的，因为计算矩形还需要计算宽度，很容易知道宽度是由下标确定的，记录了下标其实对应的高度就可以直接从输入数组中得出，因此，应该记录的是下标。
我们就拿示例的数组 [2, 1, 5, 6, 2, 3] 为例：
1. 一开始看到的柱形高度是2，这个时候以这个2为高度的最大面积的矩形还不能确定，我们需要继续向右遍历，如下图：
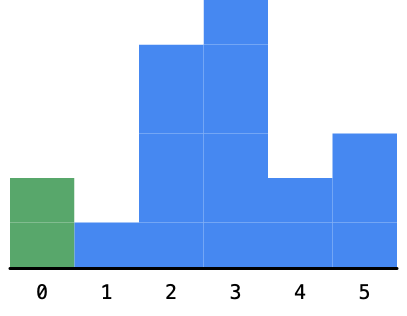
2. 然后看到高度为1的柱形，这个时候以为这个柱形为高度的矩形的最大面积还是不知道的。但是它之前的以2为高度的最大面积的矩形还是确定的，这是因为这个1比2小，因为这个1卡在了这里，导致2不能再向右扩展了，如下图：
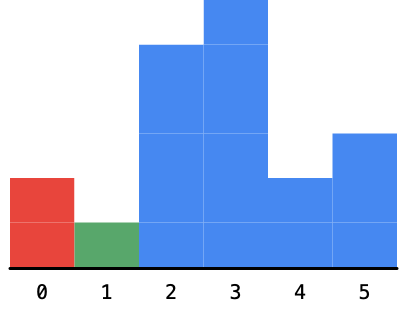
我们计算一下以2为高度的最大矩形的面积是2。其实这个时候，求解这个问题的思路其实已经慢慢打开了。如果已经确定了一个柱形的高度，我们可以无视它，将它以虚框表示，如下图：
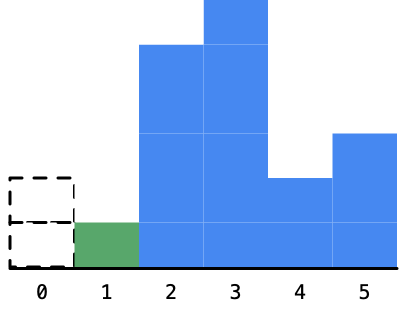
3. 遍历到高度为5的柱形，同样的以当前看到柱形为高度的矩形的最大面积也是不知道的，因为我们还要看右边高度的情况。那么它的左右有没有可以确定的柱形呢？没有，这是因为5比1大，我们看后面马上出现了6，不管是1这个柱形还是5这个柱形，都还可以向右扩展：
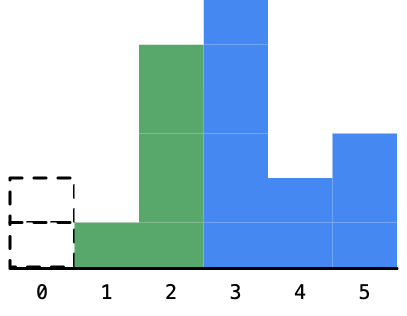
4. 接下来，遍历到高度为6的柱形，同样的，以柱形1，5，6为高度的最大矩形面积还是不能确定下来：
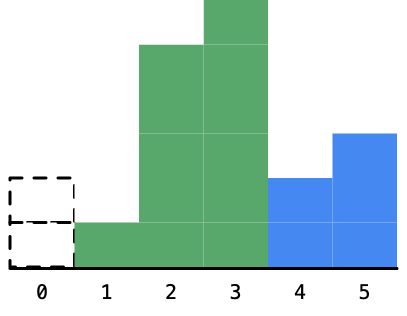
5. 再接下来，遍历到高度为2的柱形：
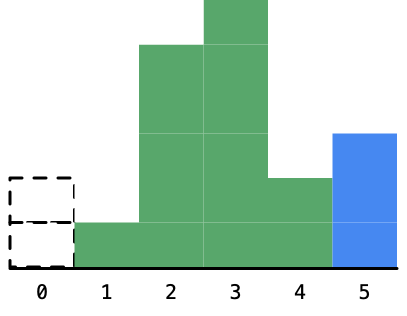
发现了一件很神奇的事情，高度为6的柱形对应的最大矩形的面积的宽度可以确定下来，它就是夹在高度为5的柱形和高度为2的柱形之间的距离，它的高度是6，宽度是1（红色柱子）:
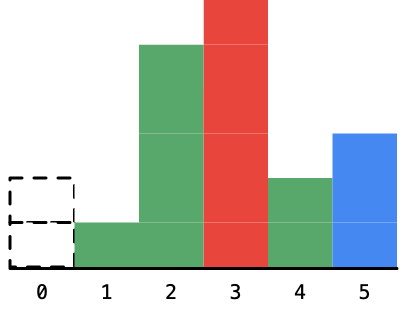
将可以确定的柱形设置为虚线：
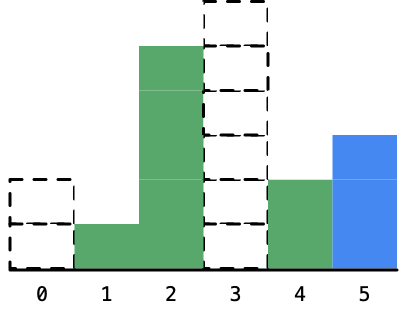
接下来柱形5对应的最大面积的矩形的宽度也可以确定下来，它是夹在高度为1和高度为2的两个柱形之间的距离（虚线柱子忽略）：
确定好以后，我们将它也标成虚线：
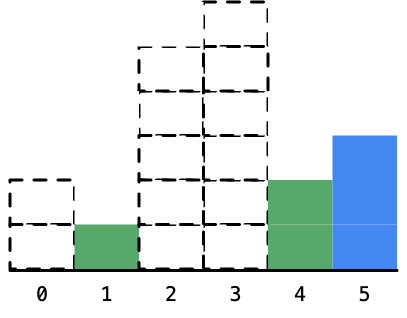
我们发现了：只要是遇到了当前柱形高度比它上一个柱形的高度严格小的时候，一定可以确定它之前的某些柱形的最大宽度，并且确定的柱形高度的顺序是从右边向左边。
这个现象告诉我们，在遍历的时候需要记录的信息就是遍历到的柱形的下标，一左一右的两个柱形的下标之差就是这个面积最大的矩形的宽度。
此时，还需要考虑的一个细节是，在确定一个柱形的面积的时候，除了右边要比当前严格小，其实还蕴含了一个条件，那就是左边也要同样比当前严格小。
那么如果是左边的高度和自己相等怎么办呢？我们想一想，我们之前是只要比当前严格小，我们才可以确定一些柱形的最大宽度，只要是大于或等于之前看到的那一个柱形的高度的时候，我们其实都不能确定。
因此我们确定当前柱形对应的宽度的左边界的时候，一定要找到第一个严格小于我们要确定的那个柱形的高度的下标。这个时候，中间那些相等的柱形其实就可以当做不存在一样。
说到这里，其实我们的思路已经慢慢清晰了。
我们在遍历的时候，需要记录的是下标，如果当前的高度比它之前的高度严格小于的时候，就可以直接确定之前的那个高的柱形的最大矩形的面积，为了确定这个最大矩形的左边界，我们还要找到第一个严格小于它的高度的矩形，向左回退的时候，其实就可以当中间这些柱形不存在一样。
因为我们就是想确定 6 的宽度，6 的宽度确定完了，其实我们就不需要它了，这个 5 的高度和这个 5 的高度确定完了，我们也不需要它了。
我们在缓存数据的时候，是从左向右缓存的，我们计算出一个结果的顺序是从右向左的，并且计算完成以后我们就不再需要了，符合后进先出的特点。因此，我们需要的这个作为缓存的数据结构就是栈。
当确定了一个柱形的高度的时候，我们就将它从栈顶移出，所有的柱形在栈中进栈一次，出栈一次，最后也一定要让栈为空，表示这个高度数组里所有的元素都考虑完了。
6. 最后遍历到最后一个柱形，即高度为3的柱形：
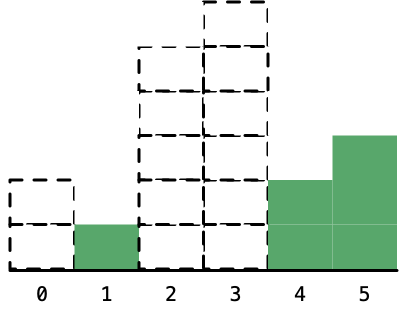
（一次遍历完成以后，接下来考虑栈里的元素全部出栈。）
接下来我们就要依次考虑还在栈里的柱形的高度。和刚才的方法一样，只不过这个时候右边没有比它高度还小的柱形了，这个时候计算宽度应该假设最右边还有一个下标为len（这里等于6）的高度为0（或者0.5，只要比1小）的柱形。
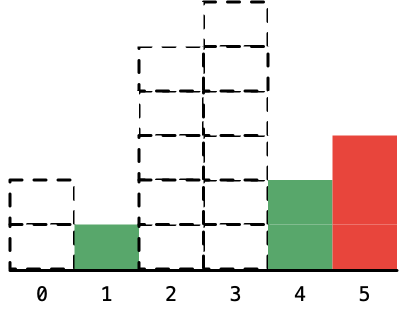
7. 下标为5，即高度为3的柱形，左边的下标是4，右边的下标是6，因此宽度是6-4-1 = 1（两边都不算，只算中间那的距离，所以减1），算完以后，将它标为虚线。
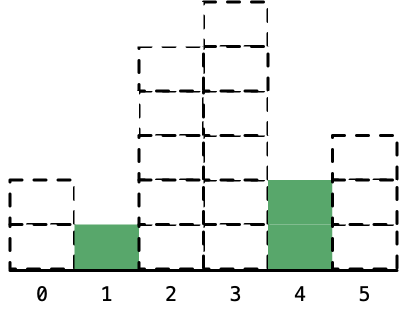
8. 下标为4高度为2的柱形，左边的下标是1，右边的下标是6，因此宽度是6-1-1 = 4。算完之后，将它标为虚线。
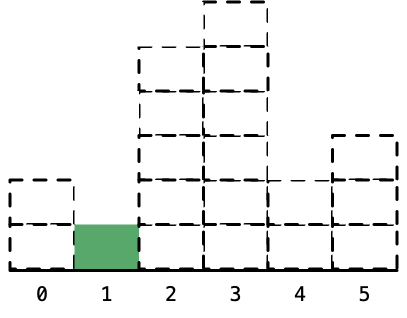
9. 最后看下标为1，高度为1的矩形，它的左边和右边其实都没有元素了，它就是整个柱形数组里高度最低的柱形，它的宽度就是整个柱形数组的长度。
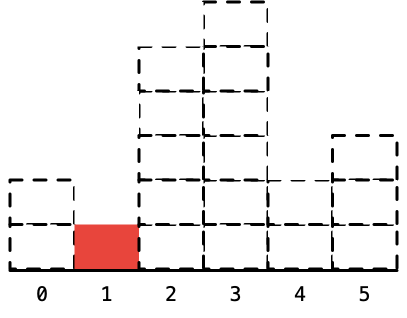
到此为止，所有的柱形高度对应的最大矩形的面积就计算出来了。
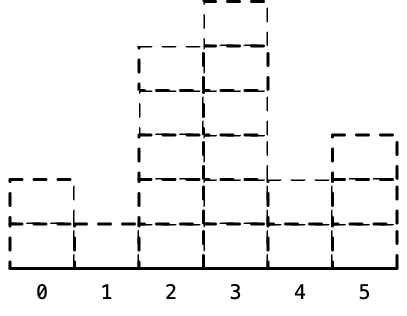
这个算法经过一次遍历，在每一次计算最大宽度的时候，没有去遍历，而是使用了栈里存放的下标信息，以O(1)的时间复杂度计算最大宽度。
from typing import List class Solution: def largestRectangleArea(self, heights: List[int]) -> int: size = len(heights) area = 0 heights = [0] + heights + [0] stack = [0] size += 2 # 这里加上数字2，因为柱子高度数组首尾的增0操作。 # i从1开始，而不是下标0开始 for i in range(1, size): while heights[i] < heights[stack[-1]]: cur_height = heights[stack.pop()] # 高 cur_width = i - stack[-1] - 1 # 宽 area = max(area, cur_height * cur_width) # 面积 stack.append(i) return area # 拿例子[2,1,5,6,2,3]试一下：==>[0,2,1,5,6,2,3,0]
