【数组&双指针】LeetCode 142. 环形链表 II【中等】

给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。

为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改链表。

示例1:

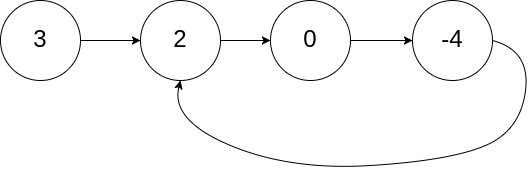
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例2：

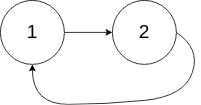
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例3:

 

 

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示：

• 链表中节点的数目范围在范围 [0, 104] 内
• -105 <= Node.val <= 105
• pos 的值为 -1 或者链表中的一个有效索引

进阶：你是否可以使用 O(1) 空间解决此题？

【分析】

这类链表题目一般都是使用双指针法解决的，例如寻找距离尾部第K个节点、寻找环入口、寻找公共尾部入口等。

算法流程：

1、双指针第一次相遇：设两指针fast，slow指向链表头部head。fast每轮走两步，slow每轮走一步。

（1）第一种结果：fast指针走过链表末端，注意是fast走过了链表末端，说明链表无环，直接返回null；

若有环，两指针一定会相遇。因为每走一轮，fast与slow的间距+1，fast终会追上slow；

（2）第二种结果：当fast == slow时，两指针在环中第一次相遇。下面分析此时fast与slow走过的步数关系：

设链表共有 a+b 个节点，其中 链表头部到链表入口 有 a 个节点（不计链表入口节点）， 链表环 有 b 个节点（这里需要注意，a 和 b 是未知数，例如图解上链表 a=4 , b=5）；设两指针分别走了 f，s 步，则有：

　　fast 走的步数是slow步数的 2 倍，即 f = 2s（fast 每轮走 2 步）；

　　fast 比 slow多走了 n 个环的长度，即 f = s + nb；（ 解析： 双指针都走过 aa 步，然后在环内绕圈直到重合，重合时 fast 比 slow 多走 环的长度整数倍 ）；　

　　以上两式相减得：s = nb，则f = s + nb = 2nb，即fast和slow 指针分别走了 2n，n个环的周长 （注意： n 是未知数，不同链表的情况不同）。

2、双指针第二次相遇

（1）slow指针位置不变，将fast指针重新指向链表头部节点；slow和fast同时每轮向前走1步（此时f=0, s=nb）；

（2）当fast指针走到f=a步时，slow指针走的步数s = a + nb，此时两指针重合，并同时指向链表环的入口。

概括一下：

根据：

1. f=2s （快指针每次2步，路程刚好2倍）

2. f = s + nb (相遇时，刚好多走了n圈）

推出：s = nb

从head结点走到入环点需要走 ： a + nb， 而slow已经走了nb，那么slow再走a步就是入环点了。

如何知道slow刚好走了a步？ 从head开始，和slow指针一起走，相遇时刚好就是a步。

时间复杂度：O(n)

空间复杂度：O(1)

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def detectCycle(self, head: ListNode) -> ListNode:
        fast, slow = head, head
        while True:
            if not (fast and fast.next):
                return 
            fast, slow = fast.next.next, slow.next
            if fast == slow:
                break
        # 两指针第二次相遇。slow指针位置不变，将fast指针重新指向链表头部节点；slow和fast同时每轮向前走1步
        fast = head
        while fast != slow:
            fast, slow = fast.next, slow.next
        return fast