【数组&双指针】leetcode4. 寻找两个正序数组的中位数【困难, 未完】

【题目】

给定两个大小分别为m和n的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数 。

算法的时间复杂度应该为O(log (m+n)) 。

 

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5
 

提示：

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106

【分析】

https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/si-wei-dao-tu-zheng-li-3chong-fang-fa-ch-osfo/

 

 

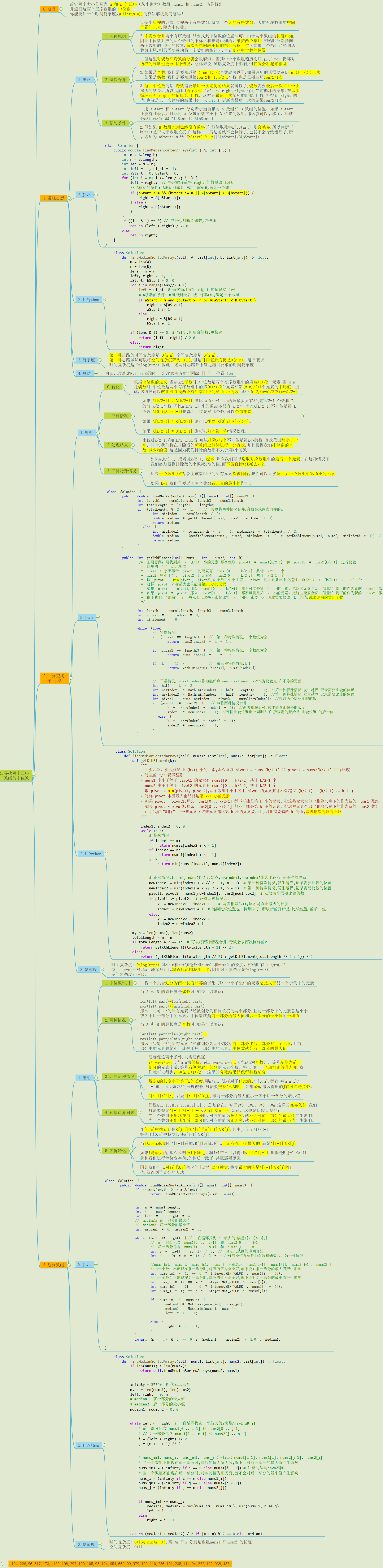
借此review一下中位数问题

1. 常规思想的改进：假合并/奇偶合并

本题的常规思想还是挺简单的：使用归并的方式，合并两个有序数组，得到一个大的有序数组。大的有序数组的中间位置的元素，即为中位数。但是这种思路的时间复杂度是O(m+n)，空间复杂度是O(m+n)，都比较高。

因此我们必须想办法将算法进行优化，这里先介绍一种简单的优化方式，就是假合并，即我们并不需要真的合并两个有序数组，只要找到中位数的位置即可。

它的思想并不复杂，由于两个数组的长度已知，因此中位数对应的两个数组的下标之和也是已知的。维护两个指针，初始时分别指向两个数组下标0的位置，每次将指向较小值的指针向后移动一位（若一个指针已达到数组末尾，则只需要移动另一个数组的指针），直到达到中位数的位置。

通过这种假合并的方式，我们可以成功将空间复杂度优化到O(1)，但是对于时间复杂度并未有什么优化。讲解这个方法的目的并不是让大家掌握该方法，而是为了让大家掌握此方法的一些巧妙的优化方式。

该方法看似容易，真正写代码的时候还是很有挑战的，不仅需要考虑奇偶问题，更要考虑一个数组遍历结束后的各种边界问题，其实很多问题就是难在了对于边界的处理上。

此方法的一个优化点就是将奇偶两种情况合并到了一起，具体思想如下：

 

 

这种思想是很有必要的, 对于数组来说, 我们经常会遇到奇偶的两种情况处理, 如果想办法将他们合并在一起, 那代码写起来就是非常顺畅和整洁.

另一种合并的思想是: 我们可以在奇数的时候, 在末尾等处添加一个占位符#等, 这样也是可以将奇数合并成偶数的情况的.

此方法的另一个优化点就是 通过在if条件中加入大量的限制条件, 从而实现了对于各种边界问题的处理, 这也是一种很重要的思想.

 

 

 

 

此方法的时间复杂度相对于下面两种思想还是太高了, 大家不用特意掌握此方法, 但是这两个优化的思想还是很重要的, 要好好的理解一下.

接下来我们就来详细讲解两个时间复杂度超低的算法代码思想。

2. 寻找第k小数 代码详解

这个思想最难的点在于 三种特殊情况的处理，我们能否想到这三种情况，并将它们完美融入到代码之中。

其实，不需要将两个数组真的合并，只需要找到中位数在哪里就可以了。

开始的思路或许是写一个循环，然后里面判断是否到了中位数的位置，到了就返回结果，但这里对偶数和奇数的分类会很麻烦。当其中一个数组遍历完后，出了for循环对边界的判断也会分几种情况。总体来说，虽然复杂度不影响，但代码看起来会很乱。

首先是怎么将奇数和偶数的情况合并一下。

用len表示合并后数组的长度，如果是奇数，我们需要知道第（len + 1）/ 2 个数就可以了，如果遍历的话需要遍历int(len/2) / + 1次。如果是偶数，我们需要知道第len/2 and (len/2) + 1个数，也是需要遍历 (len/2) + 1次。所以遍历的话，奇数和偶数都是需要遍历 (len/2) + 1次。

返回中位数的话，奇数需要最后一次遍历的结果就可以了，偶数需要最后一次和上一次遍历的结果。所以我们用两个变量left和right，right保存当前循环的结果，在每一次循环前将right的值赋给left。这样在最后一次循环的时候，left将得到right的值，也就是上一次循环的结果，接下来right更新为最后一次的结果。

循环中该怎么写？什么时候A数组后移，什么时候B数组后移。用aStart和bStart分别表示当前指向A数组和B数组的位置。如果aStart还没有遍历到最后并且此时A数组位置的数字小于B数组位置的数字，那么aStart就可以后移了。也就是aStart < m && A[aStart] < B[bStart]。

但如果B数组此刻已经没有数字了，继续取数字B[bStart]则会越界，所以此时需要判断下bStart是否大于B数组长度：

aStart < m && bStart < n || A[aStart] < B[bStart] 

如果产生越界，|| 后面的就不会执行了。

时间复杂度：遍历 len/2+1 次，len=m+n，所以时间复杂度依旧是 O(m+n)。

空间复杂度：我们申请了常数个变量，也就是 m，n，len，left，right，aStart，bStart 以及 i。

总共 8 个变量，所以空间复杂度是 O(1）。