栈和队列的高级应用--双端队列&滑动窗口
双端队列是普通队列的加强版，区别于队列只能从队头出队，队尾入队；双端队列既可以在对头入队和出队，也可以在队尾入队和出队。
下图是双端队列的图解，可以看出，双端队列既可以在队头入队和出队，也可以在队尾入队和出队。
leetcode 239. 滑动窗口最大值【困难】
给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1：
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2：
输入：nums = [1], k = 1
输出：[1]
提示：
1 <= nums.length <= 105
-104 <= nums[i] <= 104
1 <= k <= nums.length
【分析】
（1）利用双端队列记录当前滑动窗口的元素索引
（2）该双端队列最左侧元素记录滑动窗口中最大元素的索引
（3）遍历数组：
如果队列最左侧索引已不在滑动窗口区域内，弹出队列最左侧索引；
通过循环确保队列的最左侧索引对应元素值为当前窗口中最大值；
新元素入队；
从第一个滑动窗口的末尾索引开始将最大值存储到结果res中。
按照示例演示一遍，就明白逻辑了，一次不行那就多演示几次：
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
class Solution: def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]: res = [] # 定义空列表用于存储滑窗过程中统计到的最大值们 queue = collections.deque() # 定义双端队列，存放nums中元素的索引 for i, num in enumerate(nums): # 遍历输入数组 if queue and queue[0] == i - k: # 若队列非空且i与队列首个索引的间隔等于k(queue[0] - i == k,这样更好理解) queue.popleft() # 1、如果队列最左侧索引已不在滑动窗口范围内，弹出队列最左侧索引 # 这里是并行的用于大小比较的 while queue and nums[queue[-1]] < num: # 若队列非空，同时去比较滑窗中最后一个元素值与当前遍历到的元素值的大小 queue.pop() # 2、若当前遍历到的num值更大，则将队列中已有索引/正在被比较的索引出栈(即通过循环确保队列的最左侧索引所对应元素值最大) queue.append(i) # 3、新元素入队。 if i >= k - 1: # 4、从第一个滑动窗口的末尾索引开始将最大值存储到结果res中 res.append(nums[queue[0]]) return res # 复杂度分析 # 时间复杂度：O(n)，每一个下标均被放入队列一次，最多被弹出队列一次 # 空间复杂度：算返回值：O(max(n - k, k))，不算返回值：O(k)
leetcode3. 无重复子串的最长子串【中等】
给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。
示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。
提示：
0 <= s.length <= 5 * 104
s 由英文字母、数字、符号和空格组成
【分析】
使用滑动窗口的思想解决。
先用一个例子考虑如何在较优的时间复杂度内通过本题。
不妨以示例1中的字符串“abcabcbb”为例，找出从每一个字符开始的，不包含重复字符的最长子串。那么其中最长的那个字符串即为答案。对于示例1中的字符串，我们列举出这些结果，其中括号分别表示选中的字符以及以该字符为起始点得到的最长的字符串：
以 (a)bcabcbb 开始的最长字符串为 (abc)abcbb；
以 a(b)cabcbb 开始的最长字符串为 a(bca)bcbb；
以 ab(c)abcbb 开始的最长字符串为 ab(cab)cbb；
以 abc(a)bcbb 开始的最长字符串为 abc(abc)bb；
以 abca(b)cbb 开始的最长字符串为 abca(bc)bb；
以 abcab(c)bb 开始的最长字符串为 abcab(cb)b；
以 abcabc(b)b 开始的最长字符串为 abcabc(b)b；
以abcabcb(b) 开始的最长字符串为 abcabcb(b)。
发现了什么？如果我们依次递增地枚举子串的起始位置，那么子串的结束位置也是递增的。这样一来，我们就可以使用滑动窗口来解决这个问题了：
（1）我们使用两个指针分别表示字符串中的某个子串或窗口的左右边界，其中左指针代表着上文中枚举子串的起始位置，而右指针代表子串的结束位置；
（2）每一步操作中，我们会将左指针向右移动一格，表示我们开始枚举下一个字符作为起始位置，然后我们可以不断地向右移动右指针，但需要保证这两个指针对应的子串中没有重复的字符。在移动结束之后，这个子串就对应着以 左指针开始的，不包含重复字符的最长子串。我们记录下这个子串的长度；
（3）在枚举结束之后，我们找到的最长的子串的长度即为答案。
判断重复字符：
在上述流程中，我们还需要使用一种数据结构来判断是否有重复的字符，常用的数据结构为哈希集合（比如python中的set），在左指针向右移动的时候，我们从哈希表集合中移除一个字符，在右指针向右移动的时候，我们往哈希集合中添加一个字符。
class Solution: def lengthOfLongestSubstring(self, s: str) -> int: # 定义哈希集合, 记录每个字符是否出现过 occ = set() n = len(s) # 右指针，初始值为-1，相当于我们在字符串的左边界的左边的左侧，还未开始移动; ans记录无重复子串的长度。 rk, ans = -1, 0 for i in range(n): # 遍历元素 if i != 0: # 左指针向右移动一格，移除一个字符 occ.remove(s[i - 1]) while rk + 1 < n and s[rk + 1] not in occ: occ.add(s[rk + 1]) rk += 1 # 不断移动右指针 # 第i到rk个字符是一个极长的无重复字符子串 ans = max(ans, rk - i + 1) return ans # 复杂度分析 # 时间复杂度：O(N)，其中 N 是字符串的长度。左指针和右指针分别会遍历整个字符串一次。 # 空间复杂度：O(∣Σ∣)，其中 Σ 表示字符集（即字符串中可以出现的字符），∣Σ∣ 表示字符集的大小。在本题中没有明确说明字符集，因此可以默认为所有 ASCII 码在 [0, 128) 内的字符，即∣Σ∣=128。我们需要用到哈希集合来存储出现过的字符，而字符最多有∣Σ∣ 个，因此空间复杂度为 O(∣Σ∣)。
leetcode 209. 长度最小的子数组【中等】
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回0。
示例 1：
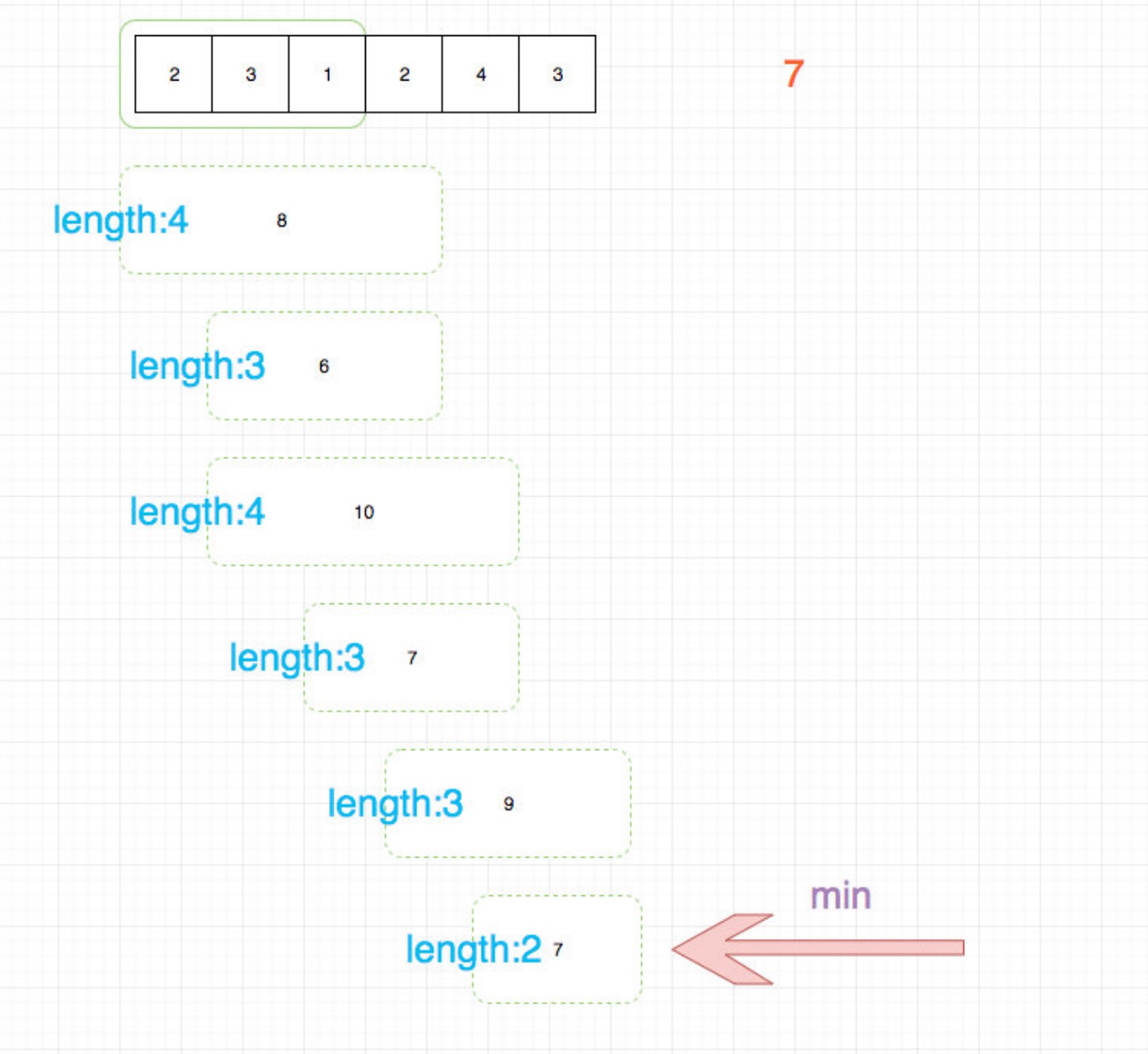
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2：
输入：target = 4, nums = [1,4,4]
输出：1
示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0
提示：
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105
进阶：
如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。
【分析】
为了较低的时间复杂度，可以使用滑动窗口的方法。
定义两个指针start和end分别表示子数组（滑动窗口）的开始位置和结束位置，维护变量sum存储子数组中的元素和（即从nums[start]到nums[end]的元素和）。
初始状态下，start和end都指向下标0，sum的值为0。
每一轮迭代，将nums[end]加到sum，若sum >= s，则更新子数组的最小长度（此时子数组的长度是end - start + 1），然后将nums[start]从sum中减去，同时将start右移，直到sum < s，在此过程中同样更新子数组的最小长度。在每一轮迭代的最后，将end右移。
class Solution: def minSubArrayLen(self, target: int, nums: List[int]) -> int: # 边界条件判断 if not nums: return 0 n = len(nums) # 获取整个数组长度 ans = n + 1 # 初始化ans, 用于记录满足条件的子数组的最小长度 start, end = 0, 0 # 初始化起始指针 total = 0 # 初始化滑动窗口数组元素和 while end < n: # 遍历 total += nums[end] # 首先计算滑窗元素和 while total >= target: # 若滑动窗口中元素之和大于等于目标s ans = min(ans, end - start + 1) # 统计长度 total -= nums[start] # 元素综合减去左指针所指元素值 start += 1 # 将滑动窗口左边界右移（因为滑动窗口中元素之和大于等于目标s），先缩小滑窗。 end += 1 # 滑动窗口右边界右移 return 0 if ans == n + 1 else ans # 复杂度非分析 # 时间复杂度：O(n)，其中n为数组长度。指针start和end最多各移动n次。 # 空间复杂度：O(1)。
