链表

介绍

链表的出现是为了解决数组（线性表）插入、删除带来的线性开销。

区别于数组，链表中的元素可以不连续存储，每一个元素包含该元素的数据和指向链表下一个节点的指针。

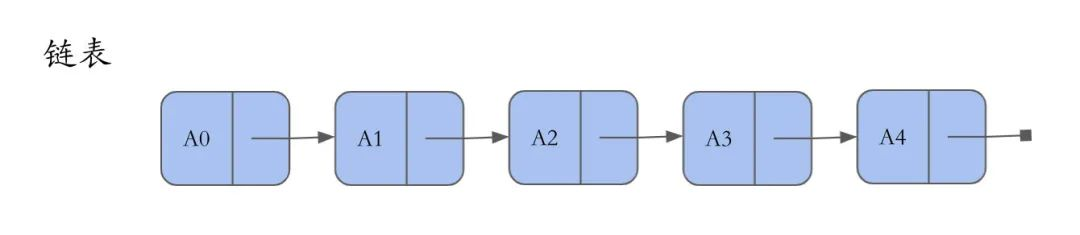
基本操作

插入

插入元素，要将插入元素X前一个位置的指针指向插入元素本身，将插入元素X的指针指向下一个位置。

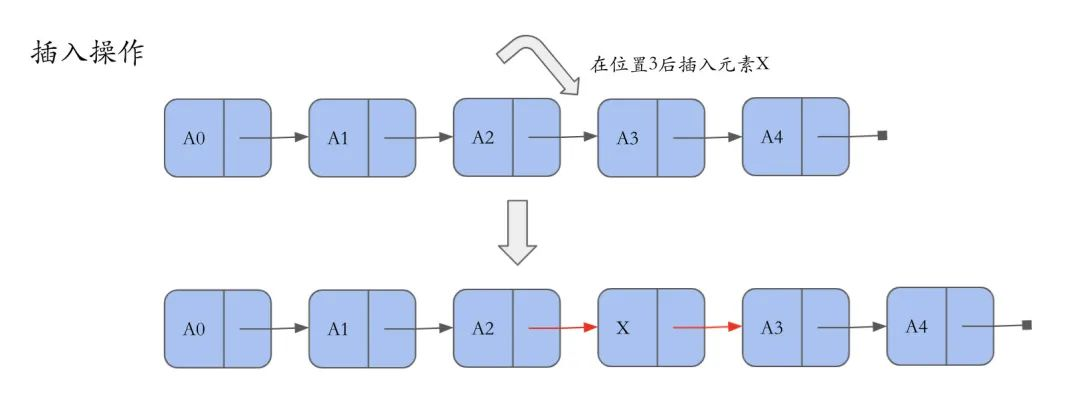
删除

删除元素，要将删除元素前一个元素的指针指向删除元素后一个元素，代码实现上需要将删除元素指针指向的位置记录下来。

下图是以长度为5的链表，删除位置3上的元素为例子。

翻转

翻转链表，可以一边遍历，同时用一个临时变量记录当前元素的下一个元素的指针所指向的位置，然后再将当前元素的下一个元素的指针指向自己。

下图是以长度为5的链表，进行链表翻转的例子。

 

 

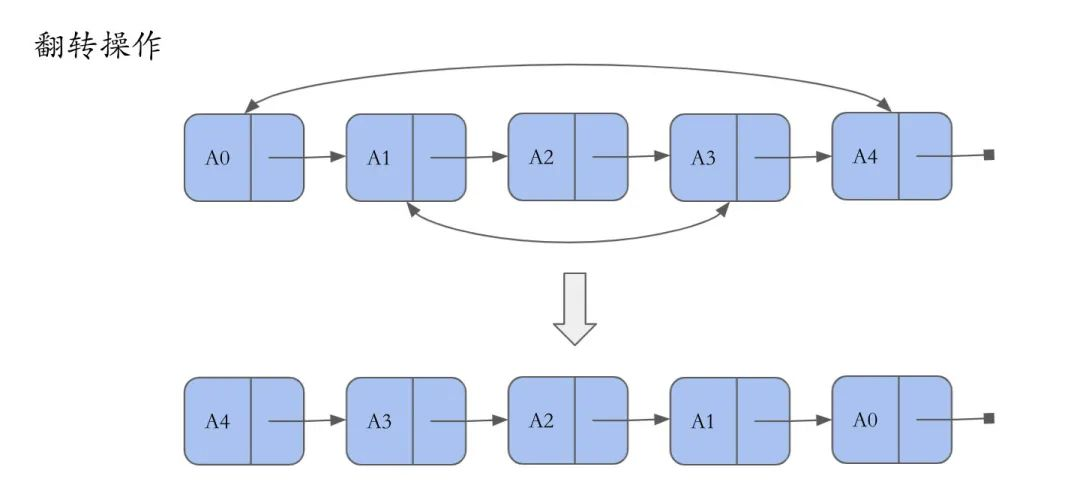
【例题】

leetcode206. 反转链表【简单】

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

提示：

链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000
 

进阶：链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

迭代法：

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        prev, curr = None, head # 初始化，prev指向头指针之前的位置，为空；curr指向链表第一个元素---头指针。
        while curr is not None:
            next = curr.next # 0.先把当前元素的下一个元素放到next中，相当于临时保存。
            #####三句话，但是思索明白逻辑#####
            curr.next = prev  # 1.第0步将当前元素原始的下一个元素安置妥当之后，再当前元素的next指针指向当前元素的前一个元素prev,逆转curr的next指针方向。
            # 后两步说白了，将prev和curr依次向右平移一位，形成新的prev & curr,二者是毗邻关系。
            prev = curr # prev右移一位到curr, 形成新的prev. 
            curr = next # curr右移一位到之前保存好的next, 形成新的curr. 再进行下一个while循环，直到curr==None循环结束。
            #####三句话，但是思索明白逻辑#####
        return prev

递归法（链表其实具备天然的递归特性）：

判断一个问题能不能使用递归解法，要判断它符不符合递归的三个条件。就反转链表这个问题，我们判断一下，是否符合递归的3个基本条件。

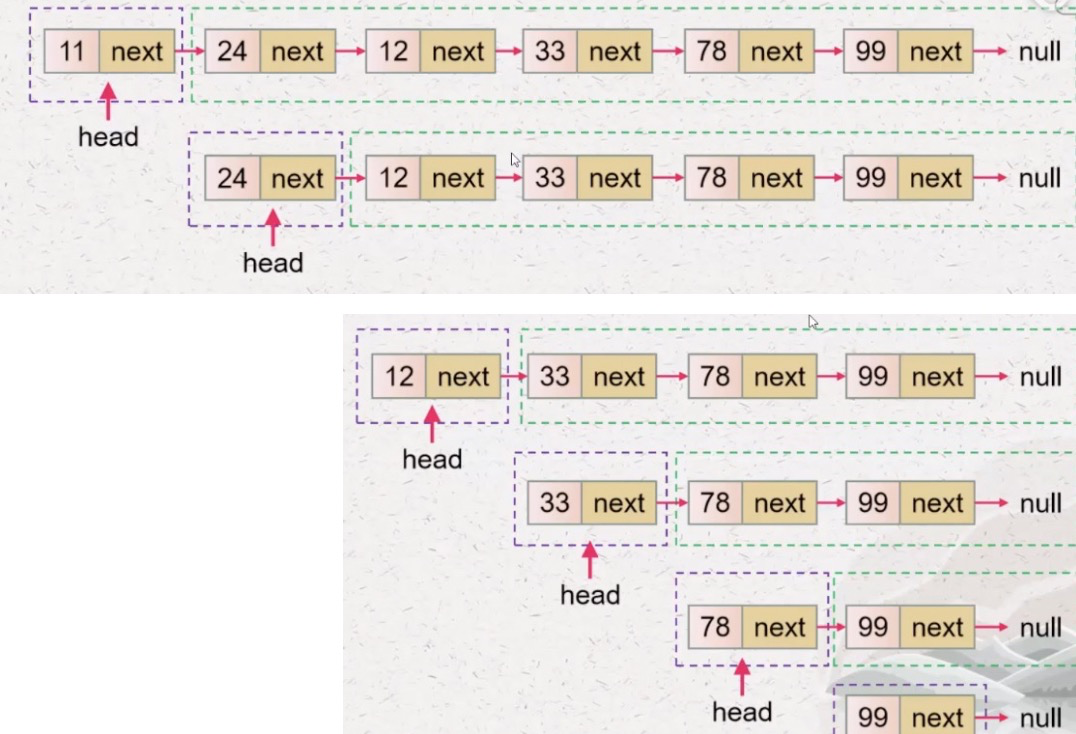
1、能不能将一个大问题拆成两个子问题？

能。如图，这里可以将反转链表视为反转头节点和除了头节点之外的其他节点的组成的一个子链表。                 

2、子问题求解方式和大问题是否一样？

一样。

3、是否存在最小子问题？

存在。一直这么拆解下去，最后只剩下一个节点，不需要反转，这个最小子问题见代码描述。

递归思路：包含两个大的过程，一个是递的过程，一个是归的过程。

递：不断将大问题拆解为子问题的过程。

归：

 

这两句。完成归的动作，首先将“head的下一个节点”的next指针指向head，然后将head的next指针指向null，完成一次反转。

开始写代码：

假设原始链表为“1->2->3->4->None”

 

首先按照子问题进行拆解，可以看到最小的子问题情况是，链表只有一个元素，比如是上面例子中的“4->None”（也可以考虑无元素），那种情况就无需反转，直接返回:

if head == None or head.next == None:
    return head

那么继续扩展一下，假设此时链表元素“递”为：“3->4->none”，我们希望反转之后结果为：“None<-3<-4”

# 首先将原始链表中，head的下一个元素的next指针指向head，这一步要很清楚我们只是在操作head的下一个元素的next指针，并未对head的next指针执行指向调整。
head.next.next = head
# 接着将head原本的next指针指向None
head.next = None

以此类推了。

完整递归写法，不再重复写注释：

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        if head is None or head.next is None:
            return head
        p = self.reverseList(head.next)
        head.next.next = head
        head.next = None
        return p

【习题1】

leetcode 237.删除链表中的节点【简单】

请编写一个函数，用于 删除单链表中某个特定节点 。在设计函数时需要注意，你无法访问链表的头节点 head ，只能直接访问 要被删除的节点 。

题目数据保证需要删除的节点 不是末尾节点 。

示例 1：

输入：head = [4,5,1,9], node = 5
输出：[4,1,9]
解释：指定链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9

示例 2：

输入：head = [4,5,1,9], node = 1
输出：[4,5,9]
解释：指定链表中值为 1 的第三个节点，那么在调用了你的函数之后，该链表应变为 4 -> 5 -> 9

提示：

链表中节点的数目范围是 [2, 1000]
-1000 <= Node.val <= 1000
链表中每个节点的值都是 唯一 的
需要删除的节点 node 是 链表中的节点 ，且 不是末尾节点！

解析：

因为题目说明，不能删除末尾节点，那么发挥一下，这道题可以用四个字形容：李代桃僵。

举例子“H->A->B->C”

你以为你删除的是A（因为你实际上不能直接将A删除掉，不然链表就断掉了），其实你可以理解为是把A的下一个相邻节点B赋值给A，然后将A的next指向A的next的next（也就是指向B的next），这样位置B就不见了（B代A僵）。也有人说，A披着B的皮囊（A处取值变为B的值）继续活在世上，恐怖且有趣。

回归现实世界，写代码：

class Solution:
    def deleteNode(self, node):
        """
        :type node: ListNode
        :rtype: void Do not return anything, modify node in-place instead.
        """
        # 这两句的操作逻辑要清晰
        node.val = node.next.val # 将要删除节点（这里称例子中的node A）的下一个节点B值赋值到node A处
        node.next = node.next.next # 将node A的next指针直接指向node的下一个节点B的下一个节点 C处（直接跳过了B，B就此不存在了）

【习题2】

leetcode 21.合并两个有序链表【简单】

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]
 

提示：

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

解析：

递归总是给人一种“只可意会不可言传”的感觉，代码一看就懂，自己一写就懵，究其原因：练习不足 & 理解不够。无妨，那就继续练习和理解。无聊解释一下，递归就是函数运行时调用自己，这个函数就叫做递归函数，调用的过程叫做递归。比如定义函数：f(x) = x + f(x-1)

def f(x):
    return x + f(x-1)

如果代入 f(2)：

返回 2+f(1)；
调用 f(1)；
返回 1+f(0)；
调用 f(0)；
返回 0+f(-1)
......
这时程序会无休止地运行下去，直到崩溃。
如果我们加一个判断语句 x > 0：

def f(x):
    if x > 0:
        return x + f(x-1)
    else: # f(0) = 0
        return 0           

这次计算 f(2)=2+f(1)=2+1+f(0)=2+1+0=3。我们从中总结两个规律：

递归函数必须要有终止条件，否则会出错；
递归函数先不断调用自身，直到遇到终止条件后进行回溯(理解回溯非常重要)，最终返回答案。

那么本题还是可以使用递归解法，满足递归的三个基础条件：可以将一个大问题拆解成两个子问题；子问题的解决方式和大问题是一样的；可以拆解出最小子问题。再加一条，有终止条件。考虑本题目：

终止条件：当两个链表均为空时，表示两个链表合并完成。

递归过程：判断两个链表l1和l2的头节点哪个更小，然后较小节点的next指针指向剩下部分节点的合并结果。

class Solution:
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        if list1 is None: return list2
        if list2 is None: return list1
        if list1.val <= list2.val: # 注意存在等于的情况
            list1.next = self.mergeTwoLists(list1.next, list2)
            return list1 # 以list1为基准，在list1上操作，所以返回list1
        else:
            list2.next = self.mergeTwoLists(list1, list2.next)
            return list2 # 以list2为基准，在list2上操作，所以返回list2

递归以及回溯过程：

1->4->5->null, 1->2->3->6->null # 因为l1.val <= l2.val
    4->5->null, 1->2->3->6->null # 所以l1.next（l1向右滚动） vs l2。之后，因为此时new l1.val > l2,以下省去new
         4->5->null, 2->3->6->null # 所以l1 vs l2.next（l2向右滚动）。之后，因为此时l1.val > l2
             4->5->null, 3->6->null # 所以继续l1 vs l2.next(l2继续向右滚动)。之后，因为此时l1.val > l2
                 4->5->null, 6->null # 所以继续l1 vs l2.next(l2继续向右滚动)。之后，看到此时l1.val < l2
                     5->null, 6->null # 此时l1.next vs l2(l1向右滚动，l2保持不动)。之后,l1.val < l2.val
                        null, 6->null # l1.next vs l2(l1继续向右，直至达到终止条件，l1已为空)
                        return l2 # l1 is empty, remain l2
                    l1.next --- 5->6->null, return l1 # 开始回溯
                l1.next --- 4->5->6->null, return l1
            l2.next --- 3->4->5->6->null, return l2
        l2.next --- 2->3->4->5->6->null, return l2
    l2.next --- 1->2->3->4->5->6->null, return l2
l1.next --- 1->1->2->3->4->5->6->null, return l1 # 直至结果完整合并完，返回。

【习题3】

leetcode 160.相交链表【简单】

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交：

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：

评测系统 的输入如下（你设计的程序 不适用 此输入）：

intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
listA - 第一个链表
listB - 第二个链表
skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

示例 1：

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
示例2:

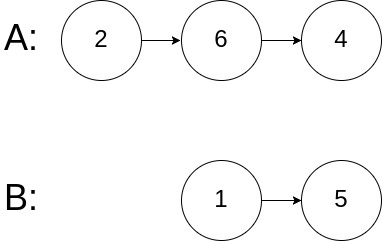
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

提示：

listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点，intersectVal 为 0
如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

进阶：你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案？

分析：

双指针解法，如果我走过你来时的路，那我们终将相遇。

设「第一个公共节点」为 node ，「链表 headA」的节点数量为 a ，「链表 headB」的节点数量为 b ，「两链表的公共尾部」的节点数量为 c ，则有：

头节点 headA 到 node 前，共有 a - c个节点；
头节点 headB 到 node 前，共有 b - c个节点；

考虑构建两个节点指针 A​ , B 分别指向两链表头节点 headA , headB ，做如下操作：

指针 A 先遍历完链表 headA ，再开始从头节点开始遍历链表 headB ，当走到 node 时，共走步数为：
a + (b - c)

指针 B 先遍历完链表 headB ，再开始从头节点开始遍历链表 headA ，当走到 node 时，共走步数为：
b + (a - c)

如下式所示，此时指针 A , B 重合，有两种情况：

a + (b - c) = b + (a - c)

若两链表 有 公共尾部 (即 c > 0 )，当指针 A , B 重合时：指针 A , B 同时指向「第一个公共节点」node 。
若两链表 无 公共尾部 (即 c = 0 )，当指针 A , B 重合时：指针 A , B 同时指向 null 。
返回 A 即可。

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        A, B = headA, headB
        while A != B:
            if A is not None:
                A = A.next
            else:
                A = headB
            
            if B is not None:
                B = B.next
            else:
                B = headA
            # 直到不满足while循环条件，也就是A = B，二指针相遇了。
        # while语句还有更加优雅的写法，只不过为了直观理解，上文展开写了
        # while A != B:
        #     A = A.next if A else headB
        #     B = B.next if B else headA
        return A