线性表

只是本人习惯在做笔记中思考，大部分都不是原创。希望你不是为了完成一道题，而是通过题目这些载体，得到一种内化的思路和解决该类问题的思维，它将能长久伴随你！

【基础知识review】

线性表概述

线性: 这里的线性是逻辑上的连续，而非物理存储的连续。

存储的数据: 线性表是一个有n个相同类型数据的有序序列。

数组基本操作

数组是物理存储连续的线性表，常见形式为：

a[0]、a[1] ... a[n-1]，a[i-1] 是 a[i] 的前驱，a[i+1] 是 a[i] 的后继。

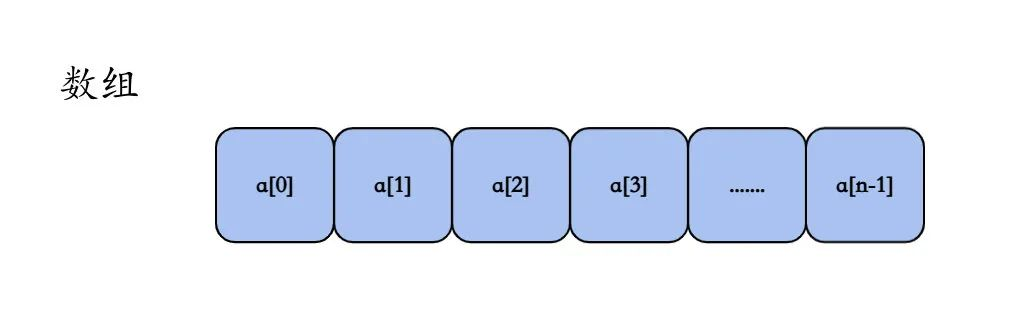
基本操作

插入：插入元素，要将插入位置后的元素全部向后移动一位。

下图以数组长度为6，数据为0、1、2、3、4、5，在位置3插入一个元素X举例。

 

 

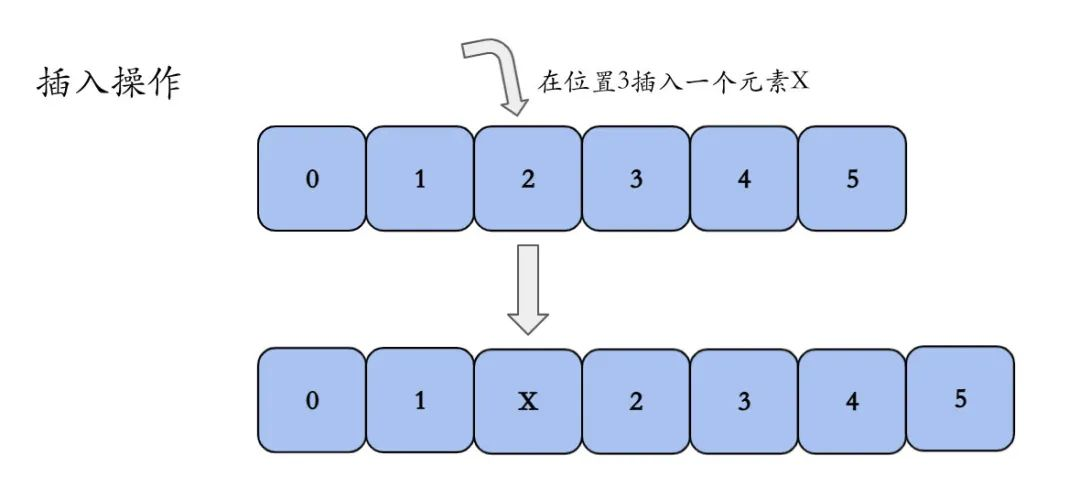
删除：删除元素，要将删除位置后的元素全部向前移动一位。

下图以数组长度为6，数据为0、1、2、3、4、5，删除位置3上的元素X举例。

 

 

 

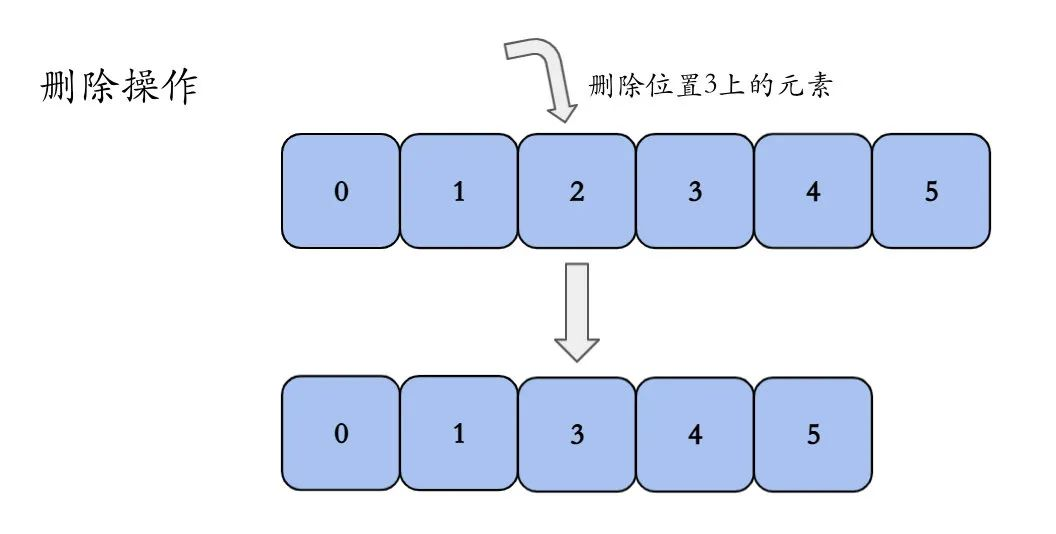
反转：反转数组，本质是将数组存储的数据进行反转。

下图以数组长度为6，数据为0、1、2、3、4、5，反转整个数组举例。

 

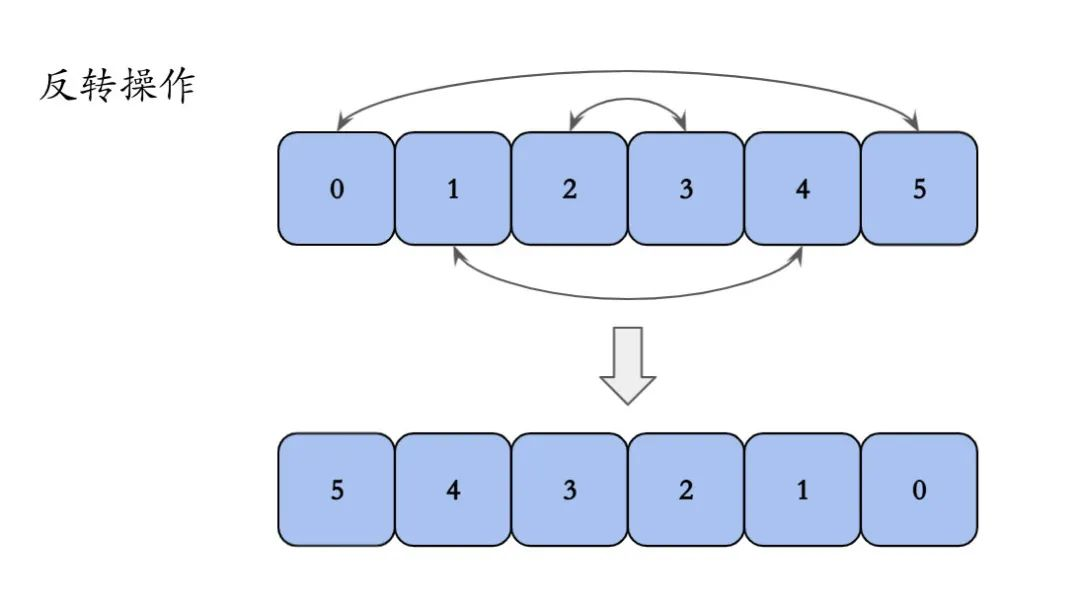
【例题1】

leetcode 27. 移除元素【简单】

题意

删除数组中所有等于val的元素，返回移除后数组的新长度。要求不使用额外的空间。

示例

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]

题解

思路导图：

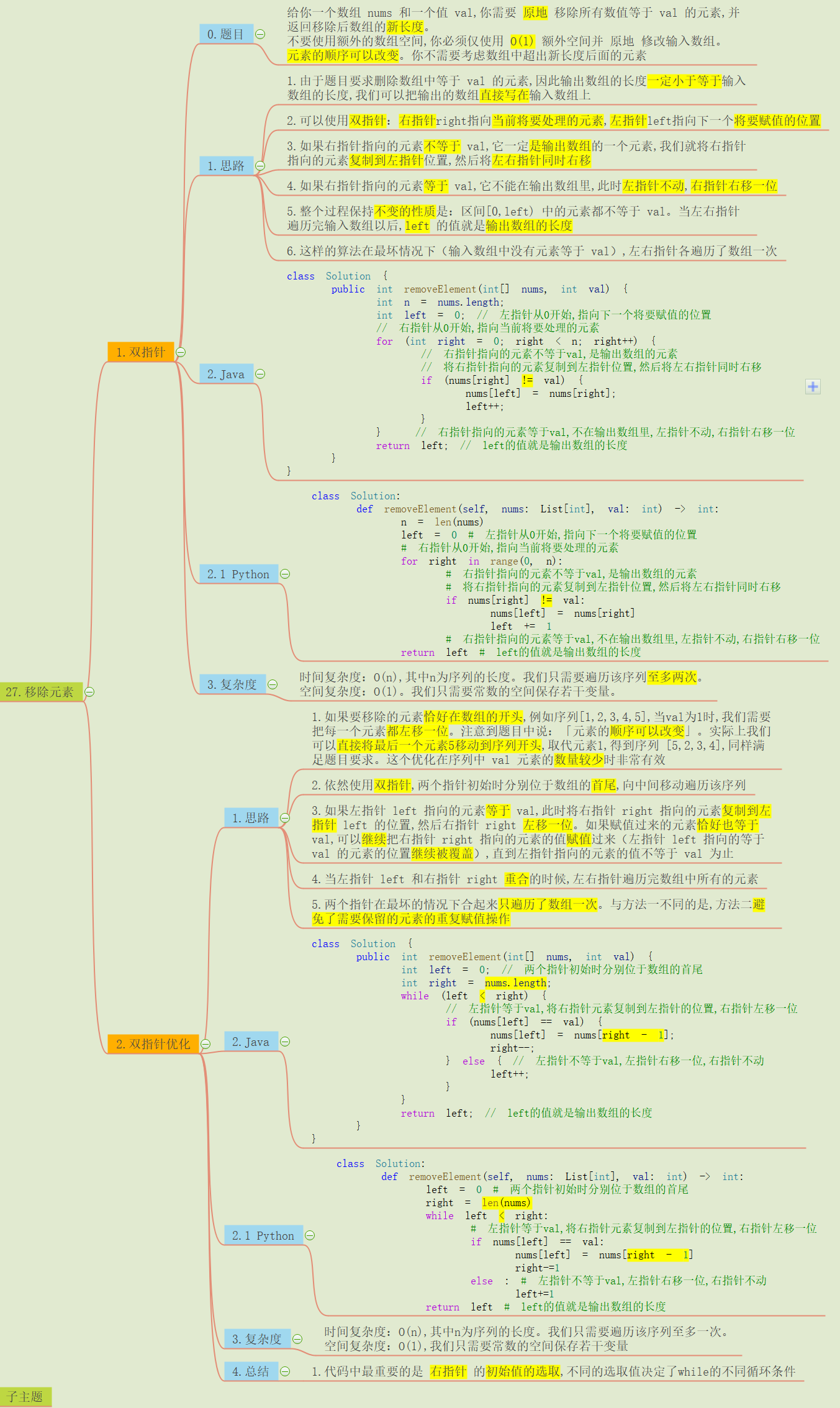
1.双指针的思想

本题最重要的条件就是原地移除元素，使用O(1)的额外空间，如果没有这个条件限制，那么本题是非常简单的，我们只需要便利一遍，将所有满足的元素放到另一个数组就完成操作了，这样就会使用到O(n)的空间复杂度。

因为限制条件的存在，我们必须寻找其他的思想，只能在原数组上进行操作，这样才能满足O(1)的空间复杂度。这样我们就不光需要找到满足条件的元素，还要同时找到满足的元素需要存放的位置，所以我们就需要使用双指针来同时确定这两个位置。

这就回到了导图中使用的思想：右指针right指向当前将要处理的元素，左指针left指向下一个将要赋值的位置。这是两个指针的作用说明。下面是两种实际遍历中会出现的情况：

（1）如果右指针指向的元素不等于val，它一定是输出数组的一个元素，我们就将右指针指向的元素复制到左指针位置，然后将左右指针同时右移

（2）如果右指针指向的元素等于val，它不能在输出数组里，此时左指针不动，右指针移动一位

在双指针进行不断遍历的过程中，我们要从变换中寻找不变的性质：区间[0，left)的元素都是不等于val的。当左右指针遍历完整个输入数组以后，left的值就是就是输出数组的长度，这样就得到了我们最终需要的结果。

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        # 双指针方法：左指针指向输出数组的元素位置，右指针指向输入数组的元素位置。
        left = 0 # 左指针初始化，指向第一个索引为0的元素
        for right in range(0, len(nums)): # 从0索引开始遍历数组元素，直至遍历至数组长度，遍历结束
            if nums[right] != val: # 若数组中元素不等于val
                nums[left] = nums[right] # 将right所指元素赋予输出数组的left位置上
                left += 1 # 输入数组的索引依次右移，继续遍历。此时for循环执行新一轮，
        return left

比较低效，优化一下。

 

2.对双指针的优化

双指针本就是非常优秀的算法了，但是本题还是可以对其再进行优化。

观察上面的算法可以发现，我们都是对满足条件（会保留下来的元素）的元素进行操作的，但是最坏的情况下，如果数组中没有任何需要移除的元素，那两个指针从头遍历到尾除了验证这一事实并未做任何实质性元素移除操作，看起来白白浪费了。而且正常情况下，需要移除的元素必然是远小于需要保留的元素，那我们直接对移除元素进行操作岂不是更有针对性。

所以，这里依然使用双指针，不同的是，两个指针初始时分别位于数组的首尾，向中间移动遍历输入数组，只是此时两指针的含义有所不同：左指针就是直接指向需要被移除的元素（数值等于val）,只要满足条件，直接使用右指针指向的元素将其替换。

这时候可能会遇到一个问题，就是如果赋值过来的元素恰好也等于val怎么办？其实这并没有什么影响，当右指针向左移动一位之后，可以继续把右指针原先指向的元素的值赋值过来（左指针指向的等于val的元素的位置继续被覆盖），直到左指针指向的元素的值不等于不等于val为止，此时左指针向右移一位。

这个方法在写代码的时候需要注意：右指针的初始值的选取（数组长度/数组长度-1），不同的选取值决定了while的不同循环条件。画个草图。

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        # 左右指针初始化
        left = 0 # 左指针指向第一个元素的索引0
        right = len(nums)  # 右指针指向数组末尾，这里从零统计索引的话，right处于末尾之后的相邻位置。边界条件
        while left < right: # 当两指针没有相遇（还未遍历完整个数组）
            if nums[left] == val: # left所指元素若等于val，将right-1所指元素赋值给left位置，如果赋值之后的值还等于val，right上的新值继续赋值给left，画个草图写一个例子，会很清晰。
                nums[left] = nums[right - 1] # 赋值给left
                right -= 1 # 右指针左移
            else:
                left += 1 # 如果左指针元素不等于val,直接右移下一位
        return right

如果右指针边界条件更改一下，代码这么写：

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        # 左右指针初始化
        left = 0 # 左指针指向第一个元素的索引0
        right = len(nums) - 1  # 右指针指向数组末尾，这里从零统计索引的话，right处于末尾之后的相邻位置。边界条件
        while left <= right: # 当两指针没有相遇（还未遍历完整个数组）
            if nums[left] == val: # left所指元素若等于val，将right-1所指元素赋值给left位置，如果赋值之后的值还等于val，right上的新值继续赋值给left，画个草图写一个例子，会很清晰。
                nums[left] = nums[right] # 赋值给left
                right -= 1 # 右指针左移
            else:
                left += 1 # 如果左指针元素不等于val,直接右移下一位
        return right+1

【例题2】

leetcode 35. 搜索插入位置【简单】

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。 

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

输入: nums = [1,3,5,6], target = 2
输出: 1

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为 无重复元素 的 升序 排列数组
-104 <= target <= 104

总结了二分查找的通用模版写法&彻底解决几个易混淆问题

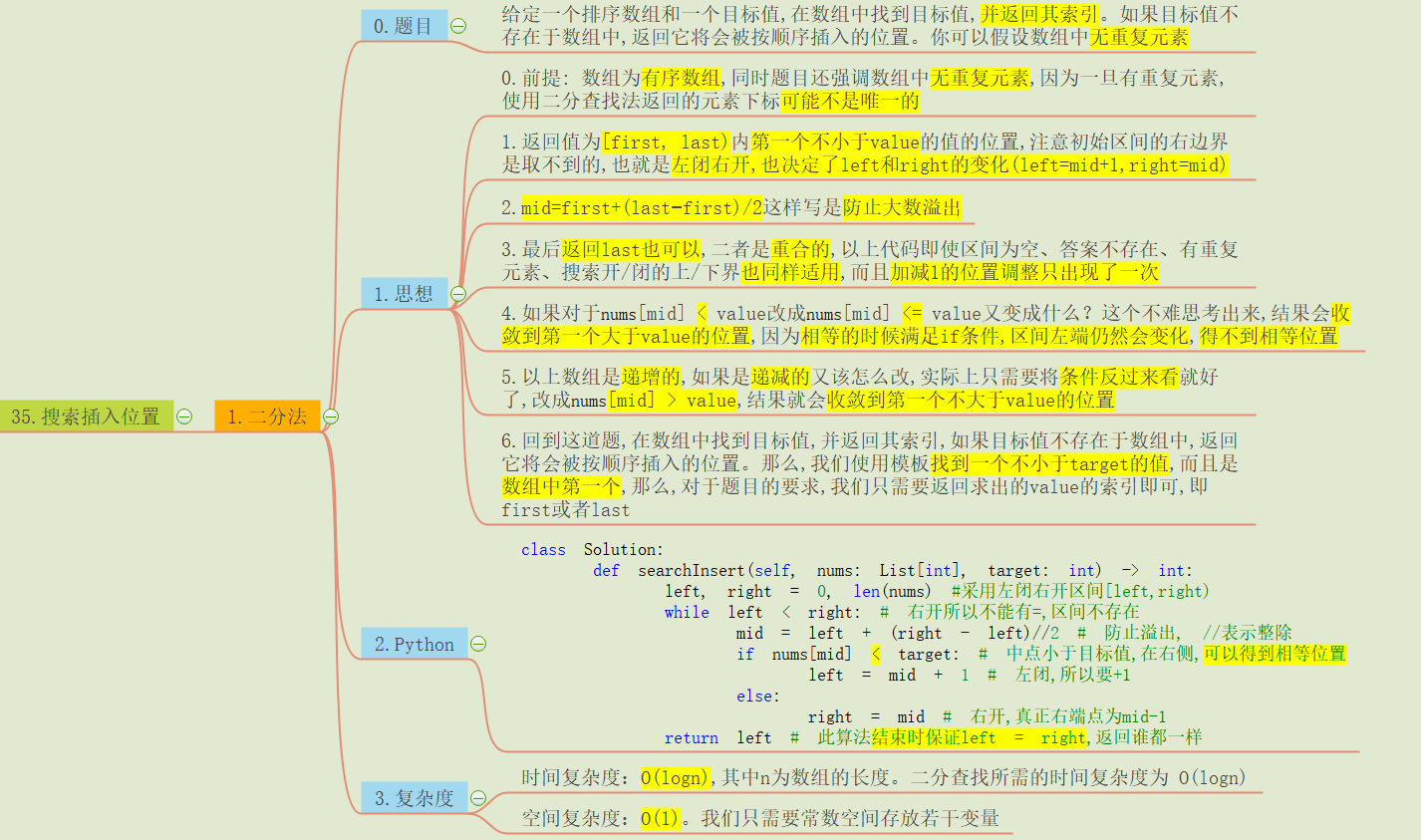
对于使用二分查找这一类题目：

1. 先确定查找区间的左右开闭情况

这是写二分查找最根本的问题，因为根据不同情况，下面的操作是完全不同的，这也是很多朋友感觉二分查找难写的地方，这里为了方便，直接将区间定义为[左闭，右开)的形式，这里根据自己的习惯最好将区间完全固定住，以后都按照一种模式来写，如果你习惯左闭右闭，也固定住，看习惯。这样不用每次都纠结。

固定为[左闭，右开)的好处是：很多函数中对区间的操作都是[左闭，右开)的形式，算是遵循这一语言特点吧，比如字符串中截取子串长度，列表的截取都是[左闭，右开)的形式，这样就可以和语言特点相对应。

另一个好处是在返回值的问题上，下文会提到。

2. 数组长度

当区间固定住为[左闭，右开)，数组长度就固定为[0，len(nums) )，这也是左右端点的初始值，如果为左闭右闭，那长度就是[0，len(nums)-1 )。

3. 循环退出条件

要特别注意，代码为while left < right，因为区间是右开，所以不能有=，这样写循环控制的另一个好处就是在退出循环的时候，必然满足left == right，因为left等于right的时候，恰好while语句不再成立，这样在最后的返回值就可以任意返回了（指return left或者return right），因为它们完全相等，而不用去纠结该返回哪个端点。

4. 中间值的写法

写法为mid = left + (right - left) // 2，//2在python中表示整除，/2在python中表示正常除法，是有余数的，这一点和其他语言有所不同。这样写的好处也显而易见面，就是为了防止大数溢出，因为写成(left + right) // 2时，当数比较大时，(left + right)是有溢出风险的，这种写法就可以避免了。

5. 中间值和目标值的比较关系

if nums[mid] < target 这个比较关系涉及到上面导图中4和5的两种变形，写成什么样的形式是不固定的，这里是根据题目要求来写的。

简单来说，就是如果是<，那么当nums[mid]达到“比target小的元素中最大的一个数”的时候，通过if条件进入，left的值为mid+1后的值，必然是大于等于target的，此时可能取到和target相等的位置。

但是换成<=时，当nums[mid] == target 时，仍然会进入if条件，left的值为mid+1后的值，必然是大于target的值（因为这里假设元素无重复），这时候就不可能取到和target相等的位置，而是会收敛到第一个大于target的位置。

导图中第五条说数组有递增变递减，其实只要将判断条件反过来，思维逻辑反过来理解一下就可以了。

6. 左右区间的变化

区间的变换完全取决于区间的定义，因为左闭，所以左区间为left=mid+1；因为右开，所以右区间为right=mid，实际上真实取的值是mid-1。

7. 最终返回值

最后的返回值上文说过，随便返回哪个都可以。

如果你也习惯或者打算习惯左闭右开的区间模式，直接理解该模版就可以了，后续需要左开右闭区间的模式，稍微更改下也就可以了。

最后，回归该题目：

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        # 二分查找（适用于有序表），以下左闭右开写法
        left = 0 # 左区间
        right = len(nums) # 右区间
        while left < right:  # 左闭右开写法，不能有等号
            mid = left + (right - left) // 2  # 中间位置索引，取整。该写法防止溢出。
            if nums[mid] < target: # 如果中间位置值小于target值，区间切块锁定右侧。
                left = mid + 1 # 左指针移动到中间位置之后一位。左闭，所以要加1。
            elif nums[mid] >= target: # # 如果中间位置值大于target值，区间切块锁定左侧。
                right = mid # 右指针移动到中间位置处。右开，直接移动到中间位置即可。
        return left  # 发现return left时间复杂度更低。 O(n)=O(log2n)