transformer first time
ref :https://jishuin.proginn.com/p/763bfbd37c6f
https://zhuanlan.zhihu.com/p/46990010
https://zhuanlan.zhihu.com/p/48508221
Transformer是Google在2017年提出的用于机器翻译的模型:

Transformer内部本质上是一个Encoder-Decoder(编码器-解码器)结构:
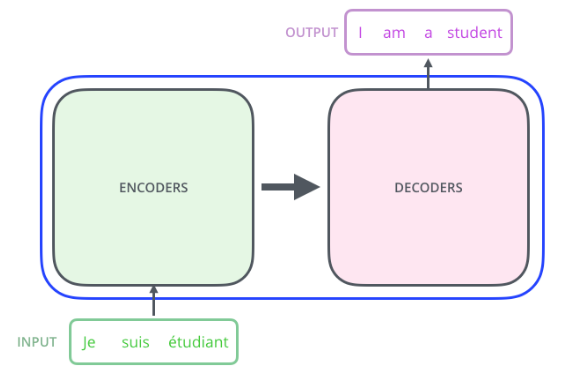
Transformer中抛弃了传统的CNN和RNN,整个网络结构完全由Attention机制组成,并且采用了6层Encoder-Decoder结构:
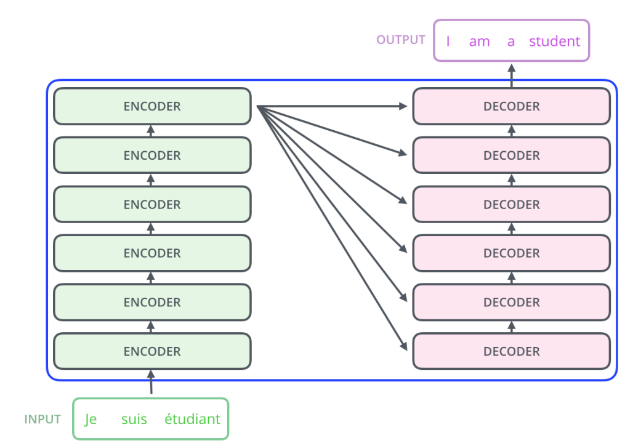
很显然了,Transformer只有分为两大部分:编码器、解码器。这里只看其中一个Encoder-Decoder结构,剩余5个一样一样的。
以一个简单的例子进行说明:
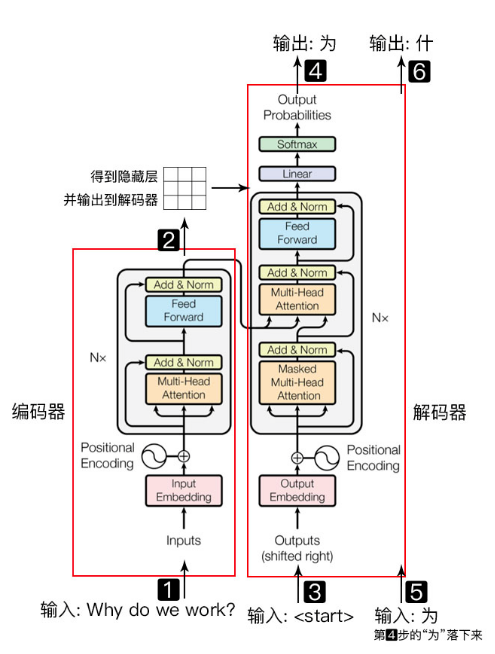
输入: Why do we work?(我们为何工作? 后面以中文字符分析)
上图左右两个红框,左侧红框是编码器Encoder,右侧红框是解码器Decoder。
编码器负责将自然语言序列映射为隐藏层(上图第2步),即含有自然语言序列的数学表达。
解码器负责将隐藏层再映射为自然语言序列,从而使我们可以解决各种问题,如情感分析、机器翻译、摘要生成、语义关系抽取等。
简单说下,上图每一步都做了什么:
输入自然语言序列到编码器:Why do we work?(为啥要工作);
编码器输出得到隐藏层,再将其输入到解码器;
输入<start>(起始)符号到解码器;
解码器得到第一个字: “为”;
将解码器得到的第一个字“为”再次从上图解码器结构的下端输入解码器;
解码器得到第二个字:“什”;
同样将解码器得到的第二个字“什”再次从上图解码器结构的下端输入解码器;
如此,直到解码器输出<end>终止符,即序列生成完成。
解码器和编码器的结构类似,本文对编码器部分进行讲解:把自然语言序列映射为隐藏层的数学表达的过程。
为便于理解学习,将编码器分为4部分依次讲解。
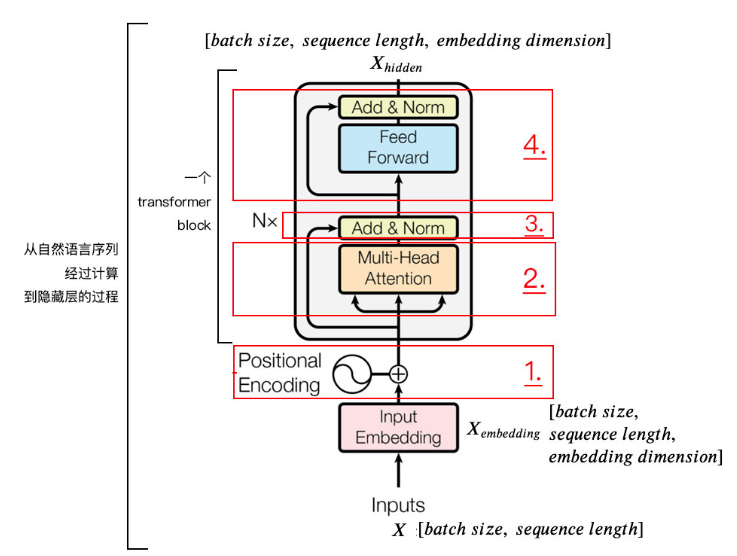
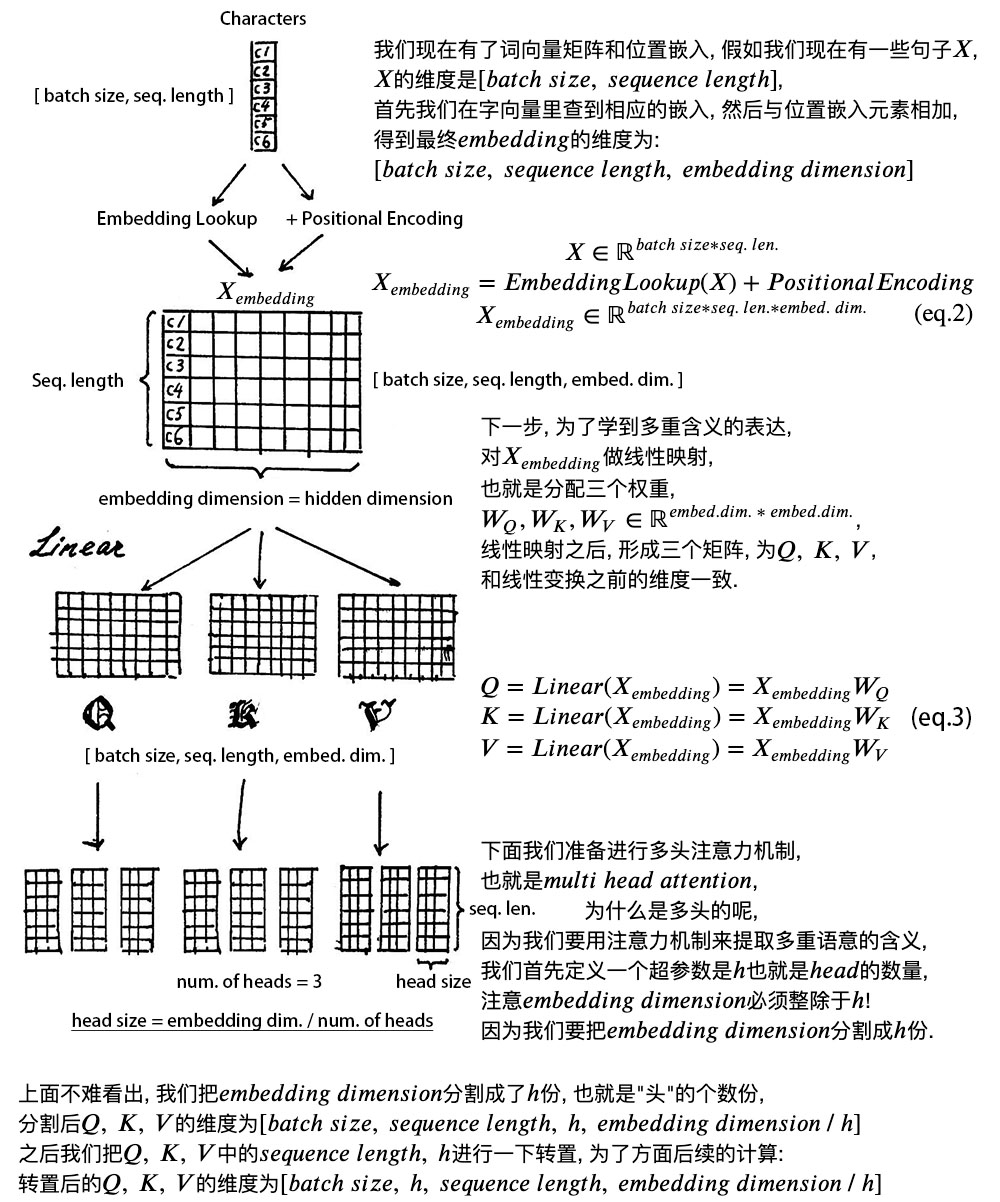
1. 位置嵌入
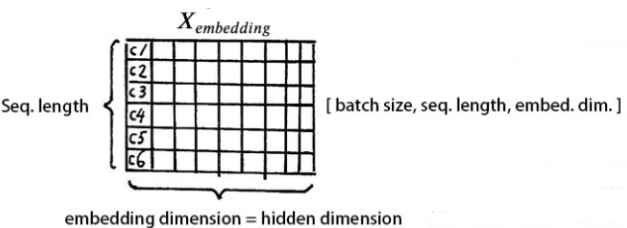
输入维度为[batch size, sequence length]的数据X,例如:我们为什么工作。
batch size就是一个batch的大小,这里只有一句话,所以batch size为1,sequence length是句子长度,共7个字,所以输入数据维度是[1,7].
我们不能直接将这句话输入到编码器中,因为transformer不认识,需要先进行字嵌入操作,得到上图中的Xembedding.
简单点说,就是文字-->字向量的转换,这种转换是将文字转换为计算机认识的数学表示,用到的方法就是Word2Vec,Word2Vec的具体细节可以暂时不用了解,知道要用到,先拿来用就好。
得到的Xembedding的维度是:[batch size, sequence length, embedding dimension]。enbedding dimension的大小由Word2Vec决定,transformer采用512长度的字向量。所以Xembedding的维度是[1, 7, 512]。
至此,输入的“我们为什么工作”,可以用一个矩阵来表示:
我们知道,文字的先后顺序,很重要。
比如吃饭没、没吃饭、没饭吃、饭吃没、饭没吃,同样三个字,顺序颠倒,所表达的含义就不同了。
--->关于Position Embedding:
因为前面说过模型本身并不包含RNN、CNN,因此无法捕捉到序列的顺序/位置信息,例如将K, V(需要先验知识:关于attention机制中Q K V三矩阵的常识)按行打乱,那么attention之后的顺序是一样的。
但是序列信息又非常重要,代表全局结构,因此必须将序列的token相对或绝对position信息利用起来。
这里每个token的position embedding 向量维度也是 然后将原本的input embedding和position embedding加起来组成最终的embedding作为encoder/decoder的输入。其中position embedding计算公式如下:
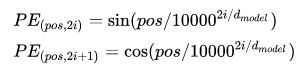
其中 表示位置index,
表示dimension index。
Position Embedding本身是一个绝对位置的信息,但在语言中,相对位置也很重要,Google选择前述的位置向量公式的一个重要原因是:由于我们有:
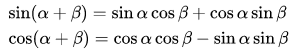
这表明位置p+k的向量可以表示成位置p的向量的线性变换,这提供了表达相对位置信息的可能性。
在其他NLP论文中,大家也都看过position embedding,通常是一个训练的向量,但是position embedding只是extra features,有该信息会更好,但是没有性能也不会产生极大下降,因为RNN、CNN本身就能够捕捉到位置信息,但是在Transformer模型中,Position Embedding是位置信息的唯一来源,因此是该模型的核心成分,并非是辅助性质的特征。
也可以采用训练的position embedding,但是试验结果表明相差不大,因此论文选择了sin position embedding,因为
- 这样可以直接计算embedding而不需要训练,减少了训练参数
- 这样允许模型将position embedding扩展到超过了training set中最长position的position,例如测试集中出现了更大的position,sin position embedding依然可以给出结果,但不存在训练到的embedding。
--->继续:
所以我们知道文字的位置信息很重要,Tranformer 没有类似 RNN 的循环结构,没有捕捉顺序序列的能力。
为了保留这种位置信息提供给 Tranformer 进行学习,我们需要用到位置嵌入。
加入位置信息的方式非常多,最简单的可以是直接将绝对坐标 0,1,2 编码。
Tranformer 采用的是 sin-cos 规则,使用了 sin 和 cos 函数的线性变换给模型提供位置信息:
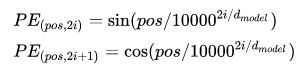
上式中,pos指的是句中字的位置,取值范围是[0, 𝑚𝑎𝑥 𝑠𝑒𝑞𝑢𝑒𝑛𝑐𝑒 𝑙𝑒𝑛𝑔𝑡ℎ),i指的是字嵌入的维度,取值范围是[0, 𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔 𝑑𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛)。 dmodel就是 𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔 𝑑𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛 的大小。
上面有 sin 和 cos 的一组公式,也就是对应着 𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔 𝑑𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛 维度的一组奇数和偶数的序号的维度,从而产生不同的周期性变化。
可以通过代码简单看下效果:
import numpy as np import matplotlib.pyplot as plt import seaborn as sns import math def get_positional_encoding(max_seq_len, embed_dim): # 初始化一个positional encoding # embed_dim: 字嵌入的维度 # max_seq_len: 最大的序列长度 positional_encoding = np.array([ [pos / np.power(10000, 2 * i / embed_dim) for i in range(embed_dim)] if pos != 0 else np.zeros(embed_dim) for pos in range(max_seq_len)]) positional_encoding[1:, 0::2] = np.sin(positional_encoding[1:, 0::2]) # dim 2i 偶数 positional_encoding[1:, 1::2] = np.cos(positional_encoding[1:, 1::2]) # dim 2i+1 奇数 # 归一化, 用位置嵌入的每一行除以它的模长 # denominator = np.sqrt(np.sum(position_enc**2, axis=1, keepdims=True)) # position_enc = position_enc / (denominator + 1e-8) return positional_encoding positional_encoding = get_positional_encoding(max_seq_len=100, embed_dim=16) plt.figure(figsize=(10,10)) sns.heatmap(positional_encoding) plt.title("Sinusoidal Function") plt.xlabel("hidden dimension") plt.ylabel("sequence length")
plt.legend()
plt.show()
可以看到,位置嵌入在 𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔 𝑑𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛 (也是hidden dimension )维度上随着维度序号增大,周期变化会越来越慢,而产生一种包含位置信息的纹理。
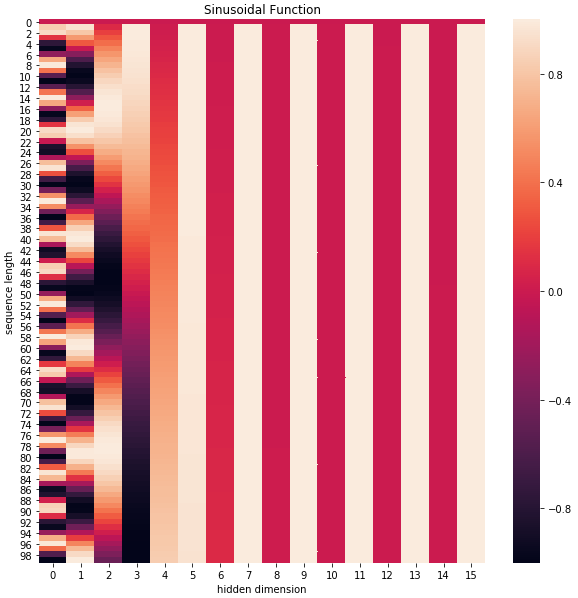
这样,产生独一的纹理位置信息,模型从而学到位置之间的依赖关系和自然语言的时序特性。最后,将 Xembedding 和 位置嵌入 相加,输入给下一层。
2. 自注意力层(self attention mechanism)
多头的意义在于,QKT得到的矩阵就叫做注意力矩阵,它可以表示,每个字与其他字的相似程度。因为向量点积值越大,表明两个向量越接近。
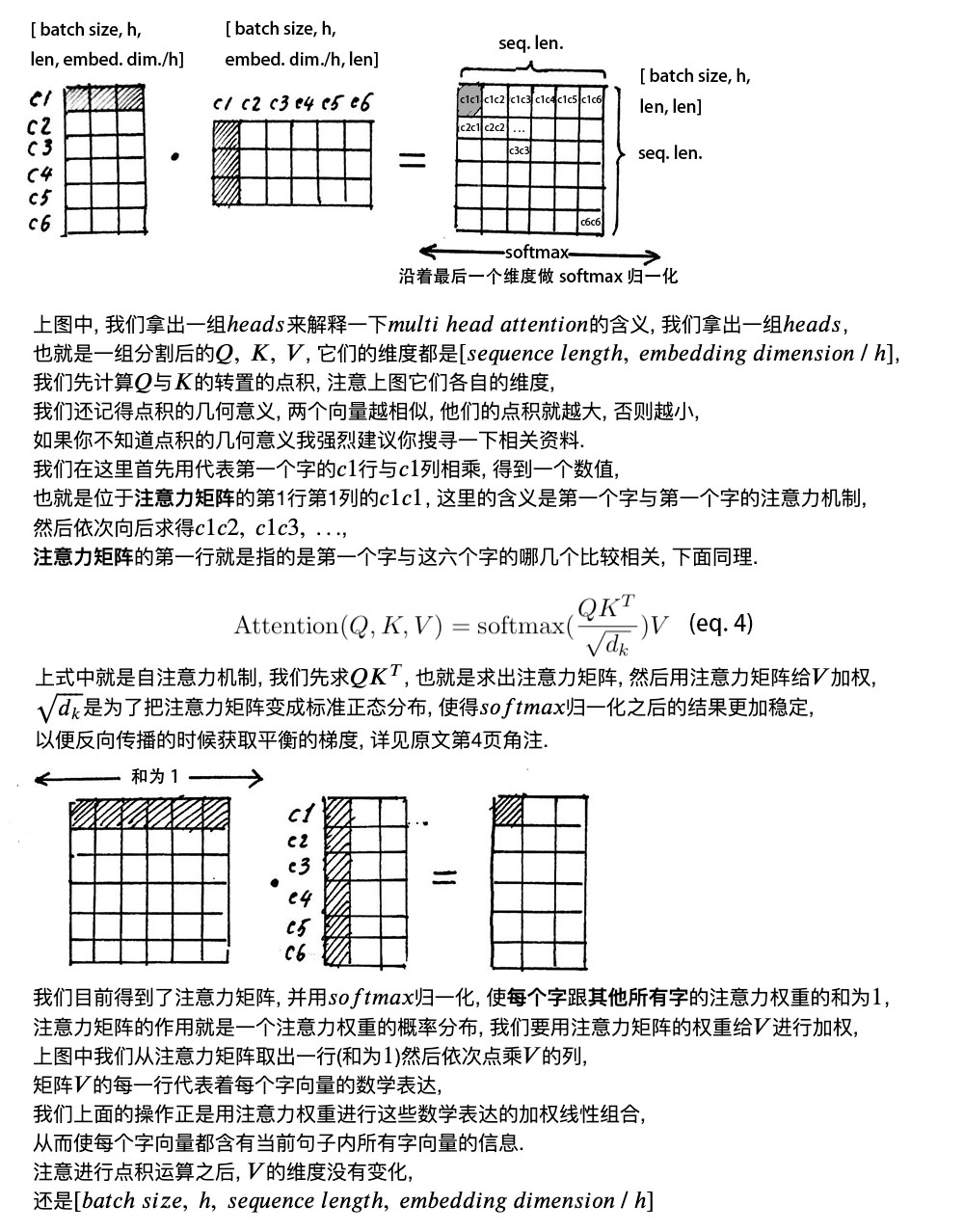
我们的目的是,让每个字都含有当前这个句子中所有字的信息,用注意力层,我们做到了。
需要注意的是,在上面 𝑠𝑒𝑙𝑓 𝑎𝑡𝑡𝑒𝑛𝑡𝑖𝑜𝑛 的计算过程中,我们通常使用 𝑚𝑖𝑛𝑖 𝑏𝑎𝑡𝑐ℎ,也就是一次计算多句话,上文举例只用了一个句子。
每个句子的长度是不一样的,需要按照最长的句子的长度统一处理。对于较短的句子,做padding操作,一般用0填充。
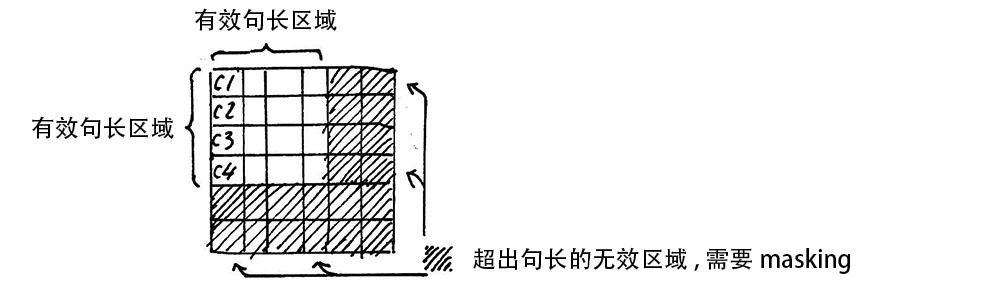
3. 残差链接和层归一化
加入了残差设计和层归一化操作,目的是为了防止梯度消失,加快收敛。
1)残差设计
我们在上一步得到了经过注意力矩阵加权之后的V,也就是Attention(Q, K, V),将其转置,使其和Xembeding维度一致,也就是[𝑏𝑎𝑡𝑐ℎ 𝑠𝑖𝑧𝑒, 𝑠𝑒𝑞𝑢𝑒𝑛𝑐𝑒 𝑙𝑒𝑛𝑔𝑡ℎ, 𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔 𝑑𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛] ,然后把他们加起来做残差连接,直接元素相加,因为他们的维度一致:
Xembeding + Attention(Q, K, V)
在之后的运算里,每经过一个模块的运算,都要把运算之前的值和运算之后的值相加,从而得到残差连接,训练的时候可以使梯度直接走捷径反传到最初始层:
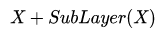
2)层归一化
作用是把神经网络中隐藏层归一为标准正态分布,也就是 𝑖.𝑖.𝑑 独立同分布, 以起到加快训练速度, 加速收敛的作用。
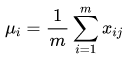
上式中以矩阵的行 (𝑟𝑜𝑤) 为单位求均值:
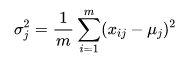
上式中以矩阵的行 (𝑟𝑜𝑤) 为单位求方差:
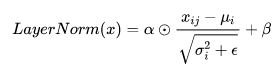
然后用每一行的每一个元素减去这行的均值,再除以这行的标准差,从而得到归一化后的数值,ε是为了防止除0;
之后引入两个可训练参数来α、β来弥补归一化过程中损失掉的信息,注意 表示元素相乘而不是点积,我们一般初始化α为全1,β为全0。
表示元素相乘而不是点积,我们一般初始化α为全1,β为全0。
代码层面非常简单,单头 attention 操作如下:
class ScaledDotProductAttention(nn.Module): ''' Scaled Dot-Product Attention ''' def __init__(self, temperature, attn_dropout=0.1): super().__init__() self.temperature = temperature self.dropout = nn.Dropout(attn_dropout) def forward(self, q, k, v, mask=None): # self.temperature是论文中的d_k ** 0.5,防止梯度过大 # QxK/sqrt(dk) attn = torch.matmul(q / self.temperature, k.transpose(2, 3)) if mask is not None: # 屏蔽不想要的输出 attn = attn.masked_fill(mask == 0, -1e9) # softmax+dropout attn = self.dropout(F.softmax(attn, dim=-1)) # 概率分布xV output = torch.matmul(attn, v) return output, attn
Multi-Head Attention 实现在 ScaledDotProductAttention 基础上构建:
class MultiHeadAttention(nn.Module): ''' Multi-Head Attention module ''' # n_head头的个数,默认是8 # d_model编码向量长度,例如本文说的512 # d_k, d_v的值一般会设置为 n_head * d_k=d_model, # 此时concat后正好和原始输入一样,当然不相同也可以,因为后面有fc层 # 相当于将可学习矩阵分成独立的n_head份 def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1): super().__init__() # 假设n_head=8,d_k=64 self.n_head = n_head self.d_k = d_k self.d_v = d_v # d_model输入向量,n_head * d_k输出向量 # 可学习W^Q,W^K,W^V矩阵参数初始化 self.w_qs = nn.Linear(d_model, n_head * d_k, bias=False) self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False) self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False) # 最后的输出维度变换操作 self.fc = nn.Linear(n_head * d_v, d_model, bias=False) # 单头自注意力 self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5) self.dropout = nn.Dropout(dropout) # 层归一化 self.layer_norm = nn.LayerNorm(d_model, eps=1e-6) def forward(self, q, k, v, mask=None): # 假设qkv输入是(b,100,512),100是训练每个样本最大单词个数 # 一般qkv相等,即自注意力 residual = q # 将输入x和可学习矩阵相乘,得到(b,100,512)输出 # 其中512的含义其实是8x64,8个head,每个head的可学习矩阵为64维度 # q的输出是(b,100,8,64),kv也是一样 q = self.w_qs(q).view(sz_b, len_q, n_head, d_k) k = self.w_ks(k).view(sz_b, len_k, n_head, d_k) v = self.w_vs(v).view(sz_b, len_v, n_head, d_v) # 变成(b,8,100,64),方便后面计算,也就是8个头单独计算 q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2) if mask is not None: mask = mask.unsqueeze(1) # For head axis broadcasting. # 输出q是(b,8,100,64),维持不变,内部计算流程是: # q*k转置,除以d_k ** 0.5,输出维度是b,8,100,100即单词和单词直接的相似性 # 对最后一个维度进行softmax操作得到b,8,100,100 # 最后乘上V,得到b,8,100,64输出 q, attn = self.attention(q, k, v, mask=mask) # b,100,8,64-->b,100,512 q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1) q = self.dropout(self.fc(q)) # 残差计算 q += residual # 层归一化,在512维度计算均值和方差,进行层归一化 q = self.layer_norm(q) return q, attn
前馈网络:
class PositionwiseFeedForward(nn.Module): ''' A two-feed-forward-layer module ''' def __init__(self, d_in, d_hid, dropout=0.1): super().__init__() # 两个fc层,对最后的512维度进行变换 self.w_1 = nn.Linear(d_in, d_hid) # position-wise self.w_2 = nn.Linear(d_hid, d_in) # position-wise self.layer_norm = nn.LayerNorm(d_in, eps=1e-6) self.dropout = nn.Dropout(dropout) def forward(self, x): residual = x x = self.w_2(F.relu(self.w_1(x))) x = self.dropout(x) x += residual x = self.layer_norm(x) return x
最后,回顾下 𝑡𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑒𝑟 𝑒𝑛𝑐𝑜𝑑𝑒𝑟 的整体结构。
经过上文的梳理,我们已经基本了解了 𝑡𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑒𝑟 编码器的主要构成部分,我们下面用公式把一个 𝑡𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑒𝑟 𝑏𝑙𝑜𝑐𝑘 的计算过程整理一下:
1)字向量与位置编码
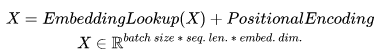
2)自注意力机制
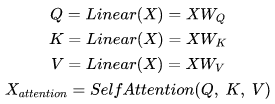
3)残差连接与层归一化
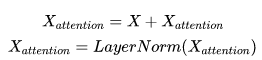
4)前向网络
其实就是两层线性激活函数,比如ReLU:
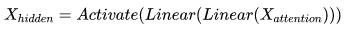
5)repeat " 3)"
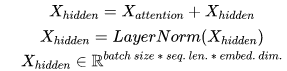
至此,我们已经讲完了 Transformer 编码器的全部内容,知道了如何获得自然语言的位置信息,注意力机制的工作原理等。

