由MAP而起
以你喜欢和理解起来最舒服的方式
以多标签图像分类任务为背景
多标签图像分类(Multi-label Image Classification)任务中图片的标签不止一个,因此评价不能用普通单标签图像分类的标准,即mean accuracy。该任务采用的是和信息检索中类似的方法——MAP(Mean Average Precision)。
MAP虽然字面意思和mean accuracy看起来差不多,但是计算方法要繁琐得多。
一、IOU(捎带介绍)
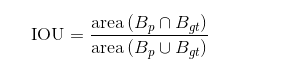
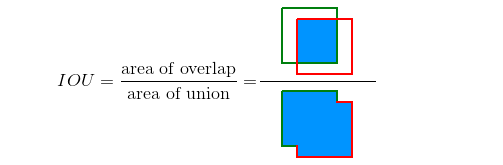
分子:两个框的交集,没有疑问。
分母:两个框的并集,这个注意数学中交集的概念——两个框的面积之和减去它们的交集面积。
二、接着说多标签图像分类,会涉及TP(True Positive)、FP(False Positive)、TN(True Negative)、FN(True Negative),Precision、Recall
(1)对TP、TN、FP、FN的(很)直观解释
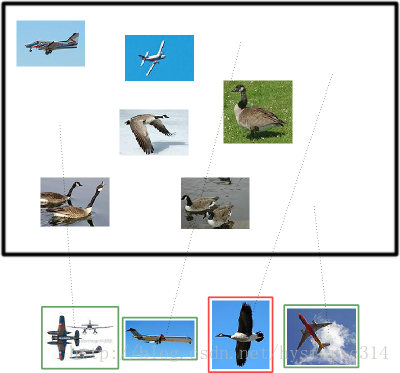
假设现在有这样一个测试集,测试集中的图片只由大雁和飞机两种图片组成,如下图所示:
假设你的分类系统最终的目的是:能取出测试集中所有飞机的图片,而不是大雁的图片。
现在做如下的定义:
True positives : 飞机的图片被正确的识别成了飞机。
True negatives: 大雁的图片没有被识别出来,系统正确地认为它们是大雁。
False positives: 大雁的图片被错误地识别成了飞机。
False negatives: 飞机的图片没有被识别出来,系统错误地认为它们是大雁。
假设你的分类系统使用了上述假设识别出了四个结果,如下图所示:
那么在识别出的这四张照片中:
True positives : 有三个,画绿色框的飞机。
False positives: 有一个,画红色框的大雁。
没被识别出来的六张图片中:
True negatives : 有四个,这四个大雁的图片,系统正确地没有把它们识别成飞机。
False negatives: 有两个,两个飞机没有被识别出来,系统错误地认为它们是大雁。
(2)对precision和recall的(很)直观解释:
push一张很有意思很形象image:
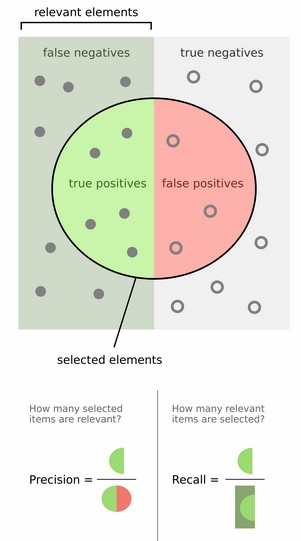
(加上一句:上面大圆圈所在四边形,左边一半都是真的(正样本),右边一半都是假的(负样本))
Precision其实就是在识别出来的图片中,True positives所占的比率:
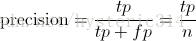
其中的n代表的是(True positives + False positives),也就是系统一共识别出来多少照片 。
在这一例子中,True positives为3,False positives为1,所以Precision值是 3/(3+1)=0.75。
意味着在识别出的结果中,飞机的图片占75%。
Recall 是被正确识别出来的飞机个数与测试集中所有飞机的个数的比值:
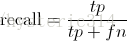
Recall的分母是(True positives + False negatives),这两个值的和,可以理解为一共有多少张飞机的照片。
在这一例子中,True positives为3,False negatives为2,那么Recall值是 3/(3+2)=0.6。
意味着在所有的飞机图片中,60%的飞机被正确的识别成飞机。
调整阈值:
你也可以通过调整阈值,来选择让系统识别出多少图片,进而改变Precision 或 Recall 的值。
在某种阈值的前提下(蓝色虚线),系统识别出了四张图片,如下图中所示:

分类系统认为大于阈值(蓝色虚线之上)的四个图片更像飞机。
我们可以通过改变阈值(也可以看作上下移动蓝色的虚线),来选择让系统识别能出多少个图片,当然阈值的变化会导致Precision与Recall值发生变化。比如,把蓝色虚线放到第一张图片下面(TP=1,FP=0,TN=5,FN=4),也就是说让系统只识别出最上面的那张飞机图片,那么Precision的值就是100% = 1/(1+0),而Recall的值则是20% = 1/(1+4)。如果把蓝色虚线放到第二张图片下面(TP=2,FP=0, TN=5,FN=3),也就是说让系统只识别出最上面的前两张图片,那么Precision的值还是100% = 2/(2+0),而Recall的值则增长到是40% = 2/(2+3)。
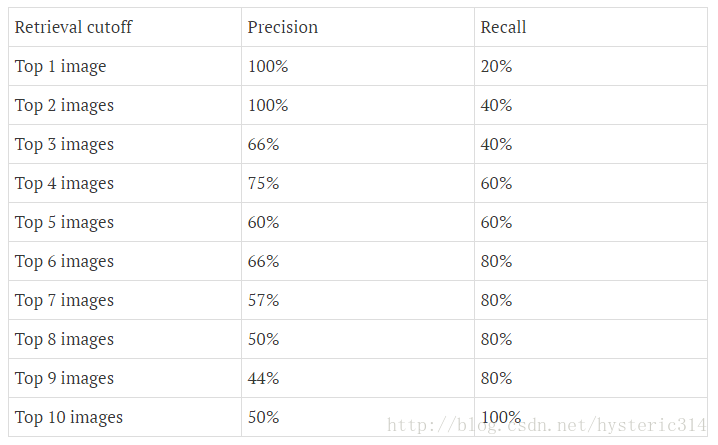
下图为不同阈值条件下,Precision与Recall的变化情况:
precision-recall曲线:
如果你想评估一个分类器的性能,一个比较好的方法就是:观察当阈值变化时,Precision与Recall值的变化情况。如果一个分类器的性能比较好,那么它应该有如下的表现:
被识别出的图片中飞机所占的比重比较大,并且在识别出大雁之前,尽可能多地正确识别出飞机,也就是让Recall值增长的同时保持Precision的值在一个很高的水平。而性能比较差的分类器可能会损失很多Precision值才能换来Recall值的提高。通常情况下,文章中都会使用Precision-recall曲线,来显示出分类器在Precision与Recall之间的权衡。
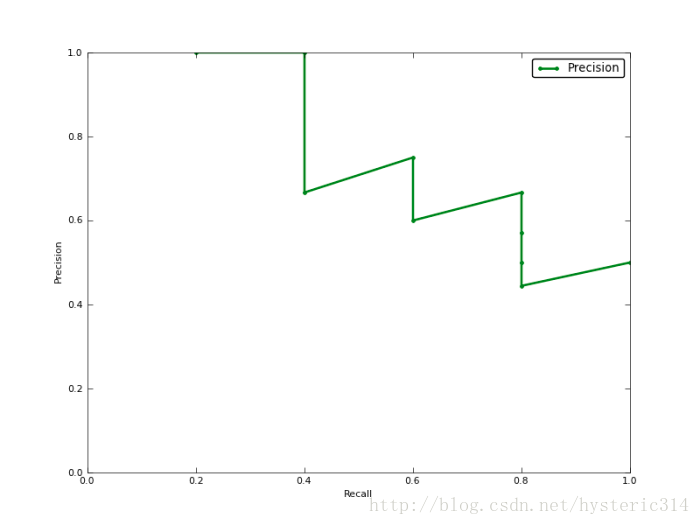
上图就是分类器的Precision-recall 曲线,在不损失精度的条件下它能达到40%Recall。而当Recall达到100%时,Precision 降低到50%。
###################################################可以先忽略##########################################################
(
Approximated Average precision
相比较与曲线图,在某些时候还是一个具体的数值能更直观地表现出分类器的性能。通常情况下都是用 Average Precision来作为这一度量标准,它的公式为:
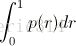
在这一积分中,其中p代表Precision ,r代表Recall,p是一个以r为参数的函数,That is equal to taking the area under the curve.
实际上这一积分极其接近于这一数值:对每一种阈值分别求(Precision值)乘以(Recall值的变化情况),再把所有阈值下求得的乘积值进行累加。公式如下:

在这一公式中,N代表测试集中所有图片的个数,P(k)表示在能识别出k个图片的时候Precision的值,而 Delta r(k) 则表示识别图片个数从k-1变化到k时(通过调整阈值)Recall值的变化情况。
在这一例子中,Approximated Average Precision的值
=(1 * (0.2-0)) + (1 * (0.4-0.2)) + (0.66 * (0.4-0.4)) + (0.75 *
(0.6-0.4)) + (0.6 * (0.6-0.6)) + (0.66 * (0.8-0.6)) + (0.57 * (0.8-0.8))
+ (0.5 * (0.8-0.8)) + (0.44 * (0.8-0.8)) + (0.5 * (1-0.8)) = 0.782.
=(1 * 0.2) + (1 * 0.2) + (0.66 * 0) + (0.75 * 0.2) + (0.6 * 0) + (0.66 * 0.2) + (0.57 * 0) + (0.5 * 0) + (0.44 * 0) + (0.5 * 0.2) = 0.782.
通过计算可以看到,那些Recall值没有变化的地方(红色数值),对增加Average Precision值没有贡献.
Interpolated Average Precision
不同于Approximated Average Precision,一些作者选择另一种度量性能的标准:Interpolated
Average
Precision。这一新的算法不再使用P(k),也就是说,不再使用当系统识别出k个图片的时候Precision的值与Recall变化值相乘。而是使用:
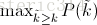
也就是每次使用在所有阈值的Precision中,最大值的那个Precision值与Recall的变化值相乘。公式如下:
下图的图片是Approximated Average Precision 与 Interpolated Average Precision相比较。
需要注意的是,为了让特征更明显,图片中使用的参数与上面所说的例子无关。
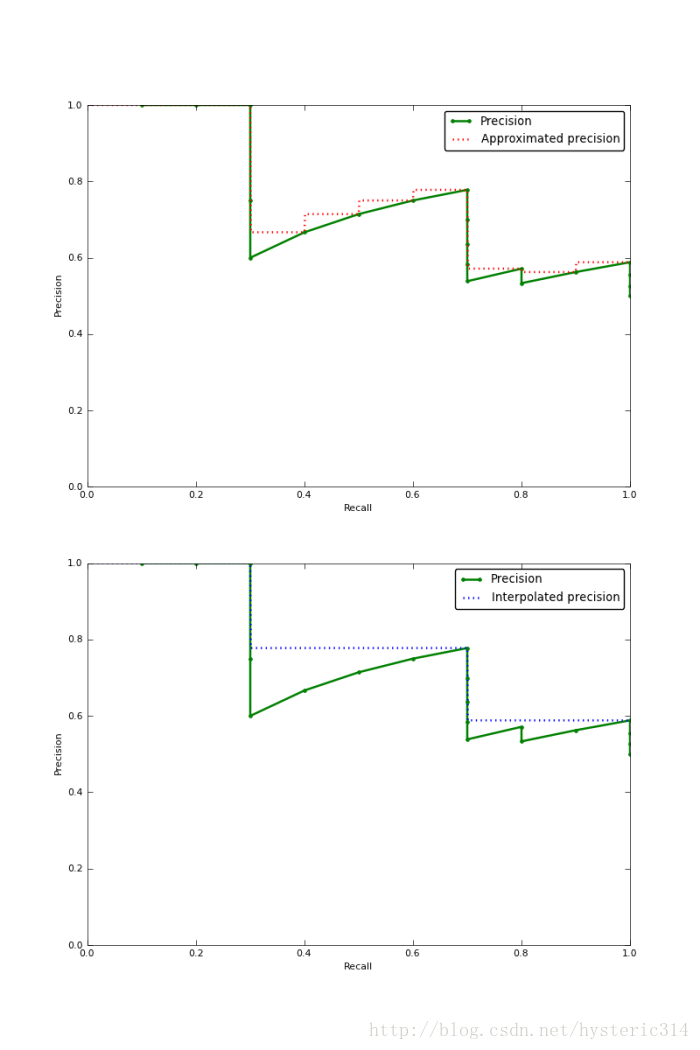
很明显 Approximated Average Precision与精度曲线挨的很近,而使用Interpolated Average
Precision算出的Average Precision值明显要比Approximated Average
Precision的方法算出的要高。
一些很重要的文章都是用Interpolated Average Precision 作为度量方法,并且直接称算出的值为Average Precision 。PASCAL Visual Objects Challenge从2007年开始就是用这一度量制度,他们认为这一方法能有效地减少Precision-recall 曲线中的抖动。所以在比较文章中Average Precision 值的时候,最好先弄清楚它们使用的是哪种度量方式。)
###################################################可以先忽略##########################################################
三. 关于AP、MAP计算
实际多类别分类任务中,我们通常不满足只通过top-N(前面说的蓝色虚线移动的操作,即在操作top数量)来衡量一个模型的好坏,而是需要知道从top-1到top-N(N是所有测试样本个数,本文中为10)对应的precision和recall。显然随着我们选定的样本越来也多,recall一定会越来越高,而precision整体上会呈下降趋势。把recall当成横坐标,precision当成纵坐标,即可得到常用的precision-recall曲线。例如某个例子的precision-recall曲线如下:
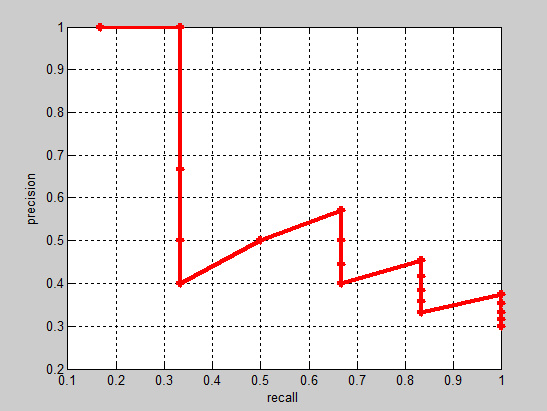
接下来说说AP的计算,此处参考的是PASCAL VOC CHALLENGE的计算方法。首先设定一组阈值,[0, 0.1, 0.2, …, 1]。然后对于recall大于每一个阈值(比如recall>=0.3),我们都会得到一个对应的最大precision。这样,我们就计算出了11个precision。AP即为这11个precision的平均值。这种方法英文叫做11-point interpolated average precision。
当然PASCAL VOC CHALLENGE自2010年后就换了另一种计算方法。新的计算方法假设这N个样本中有M个正例,那么我们会得到M个recall值(1/M, 2/M, ..., M/M)——这里还是不太好理解,或许是表达方式不够清晰,自己悟(结合下图每一个item多思考一下,可以针对每个top-N情况下的precision和recall进行计算)。对于每个recall值r,我们可以计算出对应r'(其中r' >= r)的最大precision,然后对这M个precision值取平均即得到最后的AP值(结合下面这张表和文章末尾的蓝色部分例子的内容,注意蓝色部分例子第二种AP的求取方式)。计算方法如下:

相应的Precision-Recall曲线(这条曲线是单调递减的)如下:
another eg:
(1)voc2007的计算方法:
在计算AP时,首先要把结果按照置信度排序,公式如下:

(2)voc2010的计算方法:
比起07年,10年以后的新方法是取所有真实的recall值,按照07年的方法得到所有recall/precision数据点以后,计算recall/precision曲线下的面积:
Compute a version of the measured precision/recall curve with > precision monotonically decreasing, by setting the precision for > recall r to the maximum precision obtained for any recall r′ ≥ r.
Compute the AP as the area under this curve by numerical integration. No approximation is involved since the curve is piecewise constant.
举一个例子具体说明:
对于Aeroplane类别,我们有以下输出(BB表示Bounding Box序号,IOU>0.5时GT=1):
BB | confidence | GT
----------------------
BB1 | 0.9 | 1
----------------------
BB2 | 0.9 | 1
----------------------
BB1 | 0.8 | 1
----------------------
BB3 | 0.7 | 0
----------------------
BB4 | 0.7 | 0
----------------------
BB5 | 0.7 | 1
----------------------
BB6 | 0.7 | 0
----------------------
BB7 | 0.7 | 0
----------------------
BB8 | 0.7 | 1
----------------------
BB9 | 0.7 | 1
----------------------
因此,我们有 TP=5 (BB1, BB2, BB5, BB8, BB9), FP=5 (重复检测到的BB1也算FP)。除了表里检测到的5个GT以外,我们还有2个GT没被检测到,因此: FN = 2. 这时我们就可以按照Confidence的顺序给出各处的PR值,如下:
rank=1 precision=1.00 and recall=0.14
------------------------------
rank=2 precision=1.00 and recall=0.29
------------------------------
rank=3 precision=0.66 and recall=0.29
------------------------------
rank=4 precision=0.50 and recall=0.29
------------------------------
rank=5 precision=0.40 and recall=0.29
------------------------------
rank=6 precision=0.50 and recall=0.43
------------------------------
rank=7 precision=0.43 and recall=0.43
------------------------------
rank=8 precision=0.38 and recall=0.43
------------------------------
rank=9 precision=0.44 and recall=0.57
------------------------------
rank=10 precision=0.50 and recall=0.71
------------------------------

(1)07年的方法:我们选取Recall >={ 0, 0.1, …, 1}的11处Percision的最大值:1, 1, 1, 0.5, 0.5, 0.5, 0.5, 0.5, 0, 0, 0。AP = 5.5 / 11 = 0.5
(2)VOC2010及以后的方法,对于Recall >= {0, 0.14, 0.29, 0.43, 0.57, 0.71, 1},我们选取此时Percision的最大值:1, 1, 1, 0.5, 0.5, 0.5, 0。计算recall/precision下的面积:AP = (0.14-0)x1 + (0.29-0.14)x1 + (0.43-0.29)x0.5 + (0.57-0.43)x0.5 + (0.71-0.57)x0.5 + (1-0.71)x0 = 0.5
计算出每个类别的AP以后,对于所有类别的AP取均值就得到mAP了。
AP衡量的是学出来的模型在每一个类别上的预测性能的好坏,mAP衡量的是学出来的模型在所有类别上的预测性能的好坏,得到AP后mAP的计算就很简单了,就是取所有AP的平均值。
ref(多贴几个链接):
https://github.com/rafaelpadilla/Object-Detection-Metrics#interpolating-all-points
https://blog.csdn.net/wc996789331/article/details/83785993
https://www.pianshen.com/article/4176657687/
https://blog.csdn.net/zhou4411781/article/details/105839357?utm_medium=distribute.pc_relevant_right.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param_right&depth_1-utm_source=distribute.pc_relevant_right.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param_right