MOT中的Data Association(二):最小代价流
4 最小代价流
4.1 算法形式
在了解最小代价流之前,我们需要先铺垫一下几个常见图模型,以帮助我们理解,比如最短路、最大流、最小费用最大流,最小割(闭嘴,我暂时没看懂)。下图是一个很常见的图网络:

我们可以看到,图上有很多节点和边,这两个元素是组成图模型的核心。其次,每条边上都会有对应的数值,比如最短路问题中的相邻两节点的距离,最大流中的边容量,最小费用最大流问题中的边容量和费用。那么我们来看看几个问题的具体定义:
最短路问题
最短路问题一般特指单源单汇最短路问题,即给定起点和终点,从各种路径中选择最短的路径。

上面公式中如果结合图模型来思考会简单很多,即中间节点无论会不会通过,其流入边和流出边一定有且只有0或1个,不可能经过这个点而不经过与之相邻的边。不过对于起点和终点则允许有一条流出边或一条流入边。
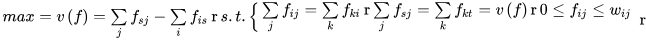
上面公式的意思是,即中间节点无论会不会通过,其流入边流量之和=流出边流量之和,从起点流出的总流量=流入终点的总流量,每条边的流量有上限。
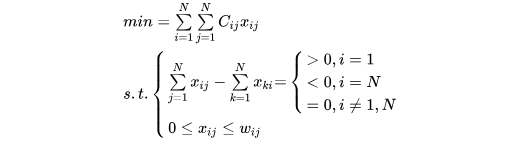
联系到多目标跟踪任务,其数据关联任务从短期来看就是一个二分图匹配问题,从长期来看就是一个图网络模型。
链接:https://zhuanlan.zhihu.com/p/111397247
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1)如果我们要用最短路模型来描述数据关联问题,其节点就是跟踪对象id,边代表跟踪轨迹和检测之间的代价。那单源单汇最短路模型就远远不足以描述,因为跟踪轨迹和检测数量是大于1的,所以从形式上来讲是多源多汇最短路,但是最短路没有限制中间节点的可重复性,所以这个问题应该用路由问题中的K –最短不相交路线(K shortest disjoint paths)来描述;
(2)如果我们要用最大流模型来描述该问题,那么不同于最短路,边容量代表跟踪轨迹和检测之间的连接可能性,所以只可能是0和1。最终要求的就是最大流量,由于边容量的限制,所以不可能重复,也就是最多可能轨迹。而且这么看来,匈牙利算法很像是最大流模型的特例;
(3)如果我们要用最小费用流模型来描述该问题,那么就跟第一部分中的最短路问题一样了,只不过多源多汇问题变成了给定初始流量的情形,距离变成了费用。最大的区别在于需要合理设定初始流量(代表了最终有多少条轨迹),还要设定边容量,不然容易所有流都流向同一条边;
(4)结合(2)(3)来看,最大流模型只需要设定跟踪轨迹和检测的连接可能性,但是缺乏了相对性。而最小费用流则只需要设定代价值,但是需要设定初始流量。这里的初始流量代表了轨迹数量,所以先用最大流模型求出最大流,即可作为初始的轨迹数量,然后再求最小费用流即可,也就是最小费用最大流。不过两个任务都有着相同的任务,那就是寻找目标轨迹,所以这样来说时间效率会较低。一般来说我们会直接使用最大流模型/最小割模型,或者直接使用最小费用流+搜索算法。
总的来说,最大流模型的优点是参数量少,但是确定跟匈牙利算法一样,我们无法对于0.9和0.5相似度的边进行相对选择,因为都是1。最小费用流模型的优点是保留了相似度,但是初始流量这一超参数不好设定。K-最短不相交路模型跟最小费用流一样,都需要设定轨迹数量。所以我们会选择用搜索算法使用最小费用流,通过搜索阈值使用最大流模型.
4.2 基于最大化后验概率模型的网络流建图
对于最小费用流而言,最难的地方在于设定初始流量和边容量,使得跟踪轨迹不交叉,而且跟踪轨迹尽可能多而合理。最重要的是,我们不知道在网络模型中哪个节点是轨迹的起点或者终点,这些都需要我们去建模。再加上我们的目标是使得代价最小,极可能最终出现每条轨迹只有一个节点的情形。
下面我们要设定几个代价值,由于每个点都有属于轨迹起点和终点的可能性,所以网络会非常大,为了更好地借鉴已有的最小费用流模型,我们可以转化为单一起点和终点的网络图:
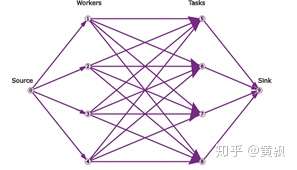
我们可以看到,简单的最小代价流结构存在几个问题:
- 一开始我们就要选定哪些节点有可能成为起点,哪些节点有可能成为终点,这无疑增加了参数量;
- 类似于最大流模型,我们通过设定边容量为1可以保证每条边最多被选择一次。但是,我们无法确保最多只有一个节点可以连接到目标节点,这就不能保证跟踪轨迹的不重叠。
针对以上问题,我们可以引入过渡节点的概念,同时也就引入了过渡边,每个节点连接一条过渡边,这样通过设定过渡边容量,可以限制每个节点的流出流量,相应地就可以限制最多只有一个节点可以连接到目标节点。而且,我们让每个节点都连接起点,每个节点的过渡节点连接终点,这样就保证上面两个问题都解决了。具体网络结构如下:
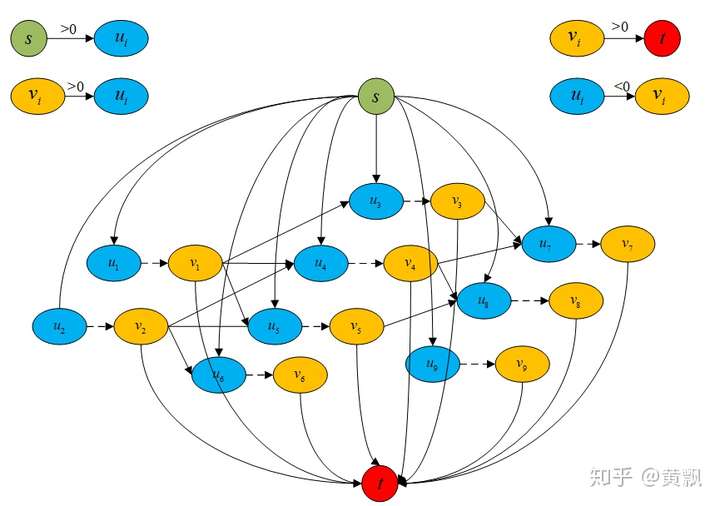
我们可以看到每个节点u都连接了起点,每个节点v都连接了终点,每个节点u都连接了过渡节点v。正如我们之前说的,每条边容量都是1,可以有效防止轨迹重叠。另外我在图中注明了每条边费用的取值范围,我们定义每条包含起点和终点的边的费用都是比较大的正数,节点与过渡节点的边的费用是负数,这样可以避免过早的终止轨迹,过渡节点与节点之间的边的费用就是跟踪轨迹和检测的代价值,取正数,不然每条轨迹都会在最后一帧终止。所以这里的参数有:初始流量的大小(轨迹数量)、节点属于轨迹起点/终点的概率、节点到过渡节点的补偿(选择这个节点的补偿)、过渡节点到节点的概率(匹配代价)。
下面我们联系多目标跟踪模型的形式来为这些参数赋予特殊的含义,首先给出后验概率形式,T表示已有轨迹,Z表示观测值:
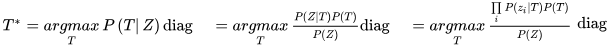
如果我们不考虑目标之间的联系,即假设目标相互独立,将联系归于代价值之中。那么上式就可以转化为:

这里我们就需要了解三个概率:
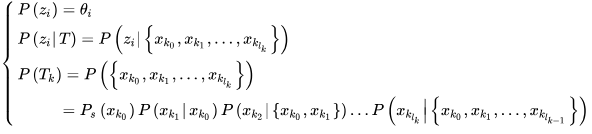
另外,我们还需要补充节点的概念来完善数据关联模型,因为上面的几个概念中我们还没有加入轨迹的终点的概率,所以明确一下联合概率数据关联模型:
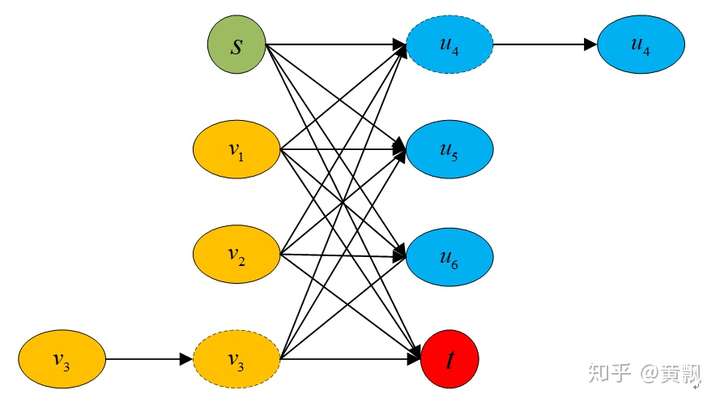
上图中虚线部分代表非当前时刻的节点,这样我们就将虚警和杂波利用起点和终点消除了,由于我们可以跨帧连接,所以虚拟目标就可以近似忽略。
接下来我们开始分析概率模型,我们可以利用对数似然概率来描述:

这里我们所说的在线和离线模型的意思是一帧一帧使用min cost flow或者多帧一起优化。对于在线的优化,我们就不需要考虑有多个节点连接同一个节点的特殊情况了,也就是说我们可以直接忽略过渡边,这样就跟KM算法一模一样了,所以我们可以认为匈牙利算法是最大流模型的特殊情况,KM算法是最小费用流的特殊情况。
接下来我们分别对在线和离线的最小代价流模型进行对比实验,其中在线最小代价流模型我们还是采用Kalman+马氏距离的方式构建代价矩阵。而离线的方式下我们则直接使用IOU和HSV直方图作为构建代价矩阵的指标。而对于观测量的概率,即决定过渡边权的指标,我们采用检测的置信度(ln(a*confidence+b))作为指标,而对于起点和终点的判定,我们将其作为超参数,连同代价阈值和特征衰减变量作为超参数。
其中特征衰减变量是对轨迹短暂消失的惩罚:
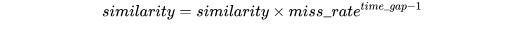
链接:https://zhuanlan.zhihu.com/p/111397247
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
另外,无论是在线跟踪还是离线跟踪,MinCostFlow这个任务本身都需要设定初始流量,也就是跟踪轨迹数量,这个值我们都知道是最少是1,最多是总id数。那么我们就需要用搜索算法来解决,为了保证求解效率,我们简单假设这个问题是一维凸优化问题,采用二分搜索或者斐波那契搜索来进行。
其中二分搜索很简单,对于斐波那契搜索,我们知道斐波那契数列{0,1,1,2,3…},即f(n)=f(n-1)+f(n-2)。对于这个通项公式,我们可以看到对于长度为f(n)的搜索空间,可以将其分为f(n-1)和f(n-2)两个部分,这样就实现了搜索空间的缩减。下面给出具体的算法:

可以看到我上面用了哈希表来存储搜索过程中的结果,避免重复运算,保证O(1)的查询效率。另外,对于求解结果,一般返回的是匹配点对,我们如何将其变成轨迹呢?这就是一个经典的“朋友圈”问题,可以采用并查集来求解,只需要O(n)的时间复杂度和O(n)的空间复杂度。不过我们这个问题简单一点,不存在一个点对应多个点的情况,所以可以简单利用数组或哈希表建立多叉树求解。
4.4 代码实现
def fibonacci(self, n): """Use Fibonacci Search to speed up Searching there can exist u~v flows(id), so we need to find the min cost flows Parameters: ----------- n: int Returns: ----------- fn: int the n th fibonacci number """ assert n > -1, "n must be non-negative number" if n in self.fib: return self.fib[n] else: return self.fib.setdefault(n, self.fibonacci(n - 1) + self.fibonacci(n - 2)) def fibonacci_search(self): """Run Fibonacci Searching to find the min cost flow Returns ------- trajectories: List[List] List of trajectories min_cost: float cost of assignments """ k = 0 r = max(0, self.max_flow - self.min_flow) s = self.min_flow cost = {} trajectories = [] # find the nearest pos of fibonacci while r > self.fibonacci(k): k = k + 1 while k > 1: u = min(self.max_flow, s + self.fibonacci(k - 1)) v = min(self.max_flow, s + self.fibonacci(k - 2)) if u not in cost: self.graph.SetNodeSupply(0, u) self.graph.SetNodeSupply(1, -u) if self.graph.Solve() == self.graph.OPTIMAL: cost[u] = self.graph.OptimalCost() else: cost[u] = np.inf if v not in cost: self.graph.SetNodeSupply(0, v) self.graph.SetNodeSupply(1, -v) if self.graph.Solve() == self.graph.OPTIMAL: cost[v] = self.graph.OptimalCost() else: cost[v] = np.inf if cost[v] == cost[u]: s = v k = k - 1 elif cost[v] < cost[u]: k = k - 1 else: s = u k = k - 2 self.graph.SetNodeSupply(0, s) self.graph.SetNodeSupply(1, -s) if self.graph.Solve() == self.graph.OPTIMAL: min_cost = self.graph.OptimalCost() / multi_factor hashlist = {0: []} # create disjoint set for arc in range(self.graph.NumArcs()): if self.graph.Flow(arc) > 0: if self.graph.Tail(arc) == 0: hashlist[0].append(self.graph.Head(arc)) else: hashlist[self.graph.Tail(arc)] = self.graph.Head(arc) for entry in hashlist[0]: tracklet = [( self.node[entry]['frame_idx'], self.node[entry]['box_idx'], self.node[entry]['box'] )] point = hashlist[entry] while point != 1: if self.node[point]['type'] == 'object': tracklet.append(( self.node[point]['frame_idx'], self.node[point]['box_idx'], self.node[point]['box'] )) if point in hashlist: point = hashlist[point] else: break trajectories.append(tracklet) else: min_cost = inf_cost return trajectories, min_cost
跟踪部分代码:
def process(self, boxes, scores, image = None, features = None, **kwargs): """Process one frame of detections. Parameters ---------- boxes : ndarray An Nx4 dimensional array of bounding boxes in format (top-left-x, top-left-y, width, height). scores : ndarray An array of N associated detector confidence scores. image : Optional[ndarray] Optionally, a BGR color image; features : Optional[ndarray] Optionally, an NxL dimensional array of N feature vectors corresponding to the given boxes. If None given, bgr_image must not be None and the tracker must be given a feature model for feature extraction on construction. **kwargs : other parameters that model needed Returns ------- trajectories: List[List[Tuple[int, int, ndarray]]] Returns [] if the tracker operates in offline mode. Otherwise, returns the set of object trajectories at the current time step. entire_trajectories: List[List[Tuple[int, int, ndarray]]] entire time steps trajectories """ # save the first node id in current frame first_node_id = deepcopy(self.node_idx) # initialize graph in every time step when online if self.mode == "online" and self.current_frame_idx > 1: self.graph = pywrapgraph.SimpleMinCostFlow() self.trajectories = [] if self.powersave: self.node = {key: self.node[key] for key in self.node \ if key not in range(2, self.last_frame_id)} for i in range(self.last_frame_id, self.node_idx): self.graph.AddArcWithCapacityAndUnitCost(0, int(i), 1, \ int(multi_factor * self.entry_exit_cost)) # Compute features if necessary. parameters = {'image': image, 'boxes': boxes, 'scores': scores, 'miss_rate': self.miss_rate, 'batch_size': self.batch_size} parameters.update(kwargs) if features is None: assert self.feature_model is not None, "No feature model given" features = self.feature_model(**parameters) # Add nodes to graph for detections observed at this time step. observation_costs = (self.observation_model(**parameters) if len(scores) > 0 else np.zeros((0,))) node_ids = [] for i, cost in enumerate(observation_costs): self.node.update({self.node_idx: { "type": 'object', "box": boxes[i], "feature": features[i], "frame_idx": self.current_frame_idx, "box_idx": i, 'cost': cost } } ) # save object node id to this time step node_ids.append(self.node_idx) if self.mode == 'online': if self.current_frame_idx == 0: self.graph.AddArcWithCapacityAndUnitCost(0, int(self.node_idx), 1, \ int(multi_factor*self.entry_exit_cost)) else: self.graph.AddArcWithCapacityAndUnitCost(int(self.node_idx), 1, 1, \ int(multi_factor * self.entry_exit_cost)) self.node_idx += 1 else: self.node.update({self.node_idx + 1: { "type": 'transition', } }) self.graph.AddArcWithCapacityAndUnitCost(0, int(self.node_idx), 1, \ int(multi_factor * self.entry_exit_cost)) self.graph.AddArcWithCapacityAndUnitCost(int(self.node_idx), int(self.node_idx + 1), \ 1, int(multi_factor * cost)) self.graph.AddArcWithCapacityAndUnitCost(int(self.node_idx + 1), 1, 1, \ int(multi_factor * self.entry_exit_cost)) self.node_idx += 2 # Link detections to candidate predecessors. predecessor_time_slices = ( self.nodes_in_timestep[-(1 + self.max_num_misses):]) for k, predecessor_node_ids in enumerate(predecessor_time_slices): if len(predecessor_node_ids) == 0 or len(node_ids) == 0: continue predecessors = [self.node[x] for x in predecessor_node_ids] predecessor_boxes = np.asarray( [node["box"] for node in predecessors]) if isinstance(features,np.ndarray): predecessor_features = np.asarray( [node["feature"] for node in predecessors]) else: predecessor_features = torch.cat( [node["feature"].unsqueeze(0) for node in predecessors]) time_gap = len(predecessor_time_slices) - k transition_costs = self.transition_model( miss_rate = self.miss_rate, time_gap = time_gap, predecessor_boxes = predecessor_boxes, predecessor_features = predecessor_features, boxes = boxes, features = features, **kwargs) for i, costs in enumerate(transition_costs): for j, cost in enumerate(costs): if cost > self.cost_threshold: continue if self.mode == 'online': last_id = int(predecessor_node_ids[i]) else: last_id = int(predecessor_node_ids[i] + 1) self.graph.AddArcWithCapacityAndUnitCost(last_id, int(node_ids[j]), 1, int(multi_factor * cost)) self.nodes_in_timestep.append(node_ids) # Compute trajectories if in online mode if self.mode == 'online': if self.current_frame_idx > 0: min_cost, n_flow = self.binary_search(high = min(len(predecessor_time_slices[0]), len(node_ids))) if n_flow > 0: self.trajectories = self.get_trajectory() else: self.trajectories = self.node2trajectory(first_node_id, self.node_idx) self.entire_trajectories = self.merge_trajectories(self.trajectories, self.entire_trajectories) else: self.trajectories = self.node2trajectory(2, self.node_idx) self.entire_trajectories = deepcopy(self.trajectories) self.current_frame_idx += 1 self.last_frame_id = first_node_id return self.trajectories, self.entire_trajectories
完整版代码:
https://github.com/nightmaredimple/libmot
在线MOTA=0.676,离线的MOTA=0.594,离线的特征关联方法很简单,而在线的用的是Kalman+马氏距离。以上都是我自己根据自己理解写的,可能理解有误,也有可能代码实现有问题。
作者:黄飘
链接:https://zhuanlan.zhihu.com/p/111397247
来源:知乎

