线性插值

插值，它根据已知的数据序列（也可以理解为坐标中一连串离散的点），找到其中的规律；然后根据找到的这个规律，来对其中尚未有数据记录的点进行数值估计。

1）它可以对数据中的缺失进行合理的补偿；2）可以对数据进行放大或者缩小。

线性插值是一种针对一维数据的插值方法，它根据一维数据序列中需要插值的点的左右邻近两个数据点来进行数值的估计。当然了它不是求这两个点数据大小的平均值（当然也有求平均值的情况），而是根据到这两个点的距离来分配它们的比重的。

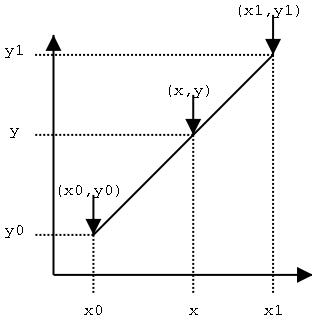
根据图中的假设：已知点(x0,y0)、(x1,y1)，试问在x处插值，y的值是多少？用我们初中学过的知识，已知两个点的坐标可以得到一条线，又已知线上一点的一个坐标可以求得这个点的另一个坐标值。这就是线性插值的原理。

 双线性插值：

在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

 假如我们想得到未知函数 f 在点 P = (x, y) 的值，假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值。最常见的情况，f就是一个像素点的像素值。首先在 x 方向进行线性插值，得到：

 

 然后在 y 方向进行线性插值，得到：

综合起来就是双线性插值最后的结果：

这样就求得了y值。

thanks：https://blog.csdn.net/u010312937/article/details/82055431#commentBox