期望、方差、协方差、相关系数

 

一、期望

在概率论和统计学中，数学期望（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和。它反映随机变量平均取值的大小。

线性运算：

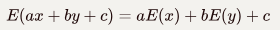
推广形式：

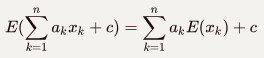
函数期望：设f(x)为x的函数，则f(x)的期望为

　　离散函数：

　　　　

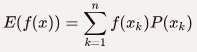
　　连续函数：

　　　　

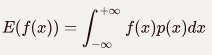
注意：

函数的期望不等于期望的函数；

一般情况下，乘积的期望不等于期望的乘积；

如果X和Y相互独立，则E(xy)=E(x)E(y)。

二、方差

概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。方差是一种特殊的期望。定义为：

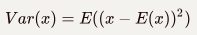
方差性质：

1）

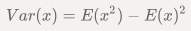
2）常数的方差为0；

3）方差不满足线性性质；

4）如果X和Y相互独立，则：

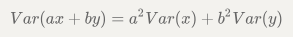
三、协方差

​协方差衡量两个变量线性相关性强度及变量尺度。 两个随机变量的协方差定义为：

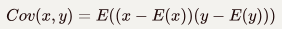
方差是一种特殊的协方差。当X=Y时，

协方差性质：

1）独立变量的协方差为0。

2）协方差计算公式：

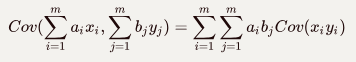
3）特殊情况：

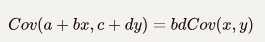
四、相关系数

相关系数是研究变量之间线性相关程度的量。两个随机变量的相关系数定义为：

相关系数的性质：

1）有界性。相关系数的取值范围是 ，可以看成无量纲的协方差。

2）值越接近1，说明两个变量正相关性（线性）越强。越接近-1，说明负相关性越强，当为0时，表示两个变量没有相关性。