最小堆

堆：一种支持数据插入删除，能方便的从中取出最大最小数据的一种高效数据结构。

假定在各个数据记录中存在一个能够标识数据记录的数据项，并将该数据项对数据进行组织，则可称此数据项为关键码。//其实对这个关键码的感念还是不太理解

如果有一个关键码的集合K={k0, k1,k2......,kn-1}，把它的所有元素按完全二叉树的顺序存储方式放在一个一维数组中，并且满足k i <= k 2i+1且k i <= k 2i+2（或者k i >= k 2i+1且k i >= k 2i+2）i = 0,1,2.....(n-2)/2 (向下取整)，则称这个集合为最小堆（或最大堆）。

如图

 

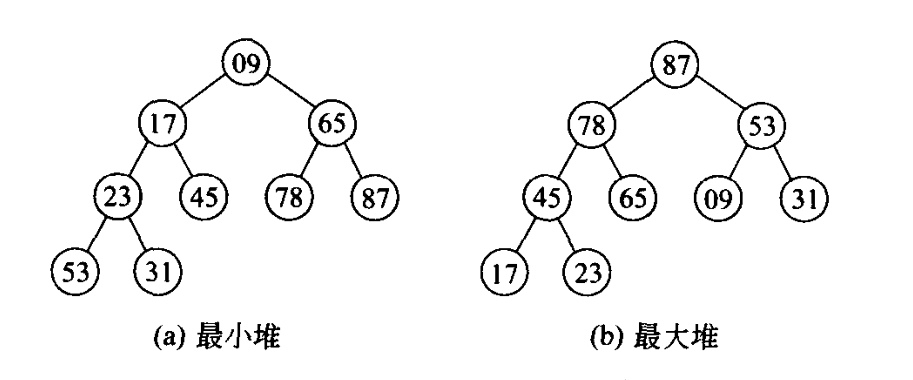
前者任意节点的关键码均小于或者等于它的左，右子女的关键码，位于堆顶的结点的关键码是整个集合最小的，所以称他为最小堆。（反之就是最大堆啦）

在我个人理解，堆，就是一种半排序的数据结构，它仅需要维持各个小分堆的堆特性，就可以保证自己的堆顶的合法性。

代码如下

//header.h
#define DefaultSize 10
#include<iostream>
using namespace std;
template<class T, class E>
class MinHeap
{
	private:
		E *heap;
		int currentSize;
		int maxHeapSize;
		void siftDown(int start, int m);
		void siftUp(int start);
	public:
		MinHeap(int sz = DefaultSize);
		MinHeap(E arr[], int n);
		~MinHeap(){delete []heap;}
		bool Insert(const E& x);
		bool RemoveMin(E& x);
		bool IsEmpty()const{return (this->currentSize == 0 ? true : false);}
		bool IsFull()const{return (this->currentSize == this->maxHeapSize ? true : false);}
		void MakeEmpty(){currentSize = 0;}
		void ShowHeap();
};

template<class T, class E>
MinHeap<T, E>::MinHeap(int sz)
{
	this->maxHeapSize = (DefaultSize < sz) ? sz : DefaultSize;
	this->heap = new E[this->maxHeapSize];
	if(this->heap == NULL)
	{
		cout<<"heap application memory failed!"<<endl;
		exit(1);
	}
	this->currentSize = 0;
}

template<class T, class E>
MinHeap<T, E>::MinHeap(E arr[], int n)
{
	this->maxHeapSize = (DefaultSize < n) ? n : DefaultSize;
	this->heap = new E[this->maxHeapSize];
	if(this->heap == NULL)
	{
		cout<<"heap application memory failed!"<<endl;
		exit(1);
	}
	for(int i=0; i<n; ++i)
		this->heap[i] = arr[i];
	this->currentSize = n;
	int currentPos = (this->currentSize-2)/2;
	while(currentPos >= 0)
	{
		siftDown(currentPos, this->currentSize-1);
		--currentPos;
	}
}

template<class T, class E>
void MinHeap<T, E>::siftDown(int start, int m)//下滑调整
{
	int  i = start, j = 2*i + 1;
	E temp = this->heap[i];
	while(j <= m)
	{
		if(i<m && this->heap[j]>this->heap[j+1])//找子节点中娇小的
			++j;
		if(temp <= this->heap[j])//与子节点较小的进行比较，发现没问题就退出
			break;
		else　　　　　　　　　　　　　　//当前堆顶比子节点大，把子节点换上来
		{
			this->heap[i] = this->heap[j];
			i = j;
			j = 2*j+1;
		}
	}
	this->heap[i] = temp;　　//交换结束，将temp放到自己合适的位置
}
template<class T, class E>
void MinHeap<T, E>::siftUp(int start)//从下到上调整
{
	if(start>this->currentSize)
	{
		cout<<"start number biger than current heap size!"<<endl;
		return;
	}
	int j = start, i = (j-1)/2;
	E temp = this->heap[j];
	while(j >= 0)
	{
		if(this->heap[i] <= temp)
			break;
		else
		{
			this->heap[j] = heap[i];
			j = i;
			i = (i-1)/2;
		}
	}
	this->heap[j] = temp;
}
template<class T, class E>
bool MinHeap<T, E>::Insert(const E& x)
{
	if(this->currentSize == this->maxHeapSize)　　//发现书中的堆太小，且不能自动扩容，加入了自动扩容功能
	{
		cerr<<"Heap Full,try application Memory!"<<endl;
		E *p = new E[this->currentSize+DefaultSize];
		if(p==NULL)
		{
			cerr<<"application memory failed!"<<endl;
			return false;
		}
		for(int i=0; i<this->currentSize; ++i)
		{
			p[i] = this->heap[i];
		}
　　　　　　　　　 delete []this->heap;　　　　//扩容后记得删除原来无用空间
		this->heap = p;
		this->maxHeapSize = this->currentSize+DefaultSize;
	}
	this->heap[currentSize] = x;
	siftDown(0, this->currentSize-1);
	++this->currentSize;
	return true;
}

template<class T, class E>
bool MinHeap<T, E>::RemoveMin(E& x)
{
	if(!this->currentSize)
	{
		cout<<"Heap empty"<<endl;
		return false;
	}
	x = this->heap[0];
	this->heap[0] = this->heap[currentSize-1];
	siftDown(0, this->currentSize-1);
	return true;
}
template<class T, class E>
void MinHeap<T, E>::ShowHeap()
{
	cout<<"Heap[] = ";
	for(int i=0; i<this->currentSize; ++i)
	{
		cout<<this->heap[i]<<" "; 
	}
	cout<<endl;
}

 

#include"header.h"

int main()
{
	int ar[] = {9,8,7,6,5,4,3,2,1,0};
	MinHeap<int, int> MH(ar, 10);
	MH.ShowHeap();
	for(int i=30; i<41; ++i)
		MH.Insert(i);
	MH.ShowHeap();
}

 运行效果

 

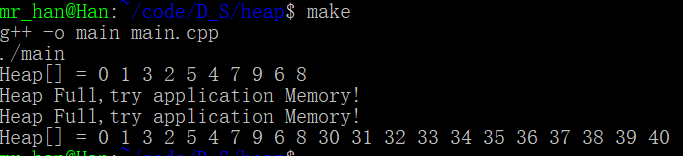
 我们将这个堆的抽象结构画出来，是这样子的