二叉树

二叉树是一种重要的基础的数据结构，其节点类型和链表有点相像，不同之处在于，它的每个节点都有两个指针，且指针有左右之分。

学习二叉树最重要的学会使用递归，和迭代对二叉树进行遍历。

程序

#include<iostream>
#include<vector>
#include"../queue/header1.h"
#include"../SeqStack/header1.h"
using namespace std;

class Node
{
	public:
		Node(char v):m_value(v),m_left(NULL),m_right(NULL),lflag(0),rflag(0){}
		char m_value;
		Node *m_left;
		Node *m_right;
		int lflag;
		int rflag;
};
class Tree
{
	public:
		Tree(char c):m_root(NULL),m_flag(c){}
		~Tree(){destroy(m_root);}
		Node *create(char *&str);
		void PreOrder(Node *root);//递归前序遍历
		void Itera_PreOrder(Node *root);//迭代前序遍历
		void inOrder(Node *root);//中序
		void postOrder(Node *root);//后序
		void levelOrder(Node *root);//层次
		void InThread(Node *&root,Node *&pre);
		void PreThreadOrder(Node *root);
		int Height(Node *root);//树高
		void destroy(Node *root);
	public:
		Node *m_root;
		char m_flag;
	protected:
		friend ostream& operator<<(ostream& out, Tree &Tree)
		{
			Node *p = Tree.m_root;
			SeqStack<Node*> S;
			S.Push(NULL);
			while(p != NULL)
			{
				cout<<p->m_value<<" ";
				if(p->m_right != NULL)
					S.Push(p->m_right);
				if(p->m_left != NULL)
					p = p->m_left;
				else
					S.Pop(p);

			}
			return out;
		}
}; 
void Tree::destroy(Node *root)
{
	if(root != NULL)
	{
		destroy(root->m_left);
		destroy(root->m_right);
		delete root;
	}
}
Node* Tree::create(char *&str)
{
	if(*str == m_flag)
		return NULL;
	else
	{
		Node *p = new Node(*str);
		p->m_left = create(++str);
		p->m_right = create(++str);
		return p;
	}
}

void Tree::PreOrder(Node *root)
{
	if(root != NULL)
	{
		cout<<root->m_value<<" ";
		PreOrder(root->m_left);
		PreOrder(root->m_right);
	}
}

void Tree::Itera_PreOrder(Node *root)
{
	SeqStack<Node*> S;
	Node	*p = root;
	S.Push(NULL);
	while(p != NULL)
	{
		cout<<p->m_value<<" ";
		if(p->m_right != NULL)
			S.Push(p->m_right);
		if(p->m_left != NULL)
			p = p->m_left;
		else
			S.Pop(p);
	}
}

void Tree::inOrder(Node *root)
{
	if(root != NULL)
	{
		inOrder(root->m_left);
		cout<<root->m_value<<" ";
		inOrder(root->m_right);
	}	
}
void Tree::postOrder(Node *root)
{
	if(root != NULL)
	{
		postOrder(root->m_left);
		postOrder(root->m_right);
		cout<<root->m_value<<" ";
	}
}

void Tree::levelOrder(Node *root)
{
	SeqQueue<Node*> Q;
	Node *p = root;
	Q.EnQueue(p);
	while(!Q.IsEmpty())
	{
		Q.DeQueue(p);
		cout<<p->m_value<<" ";
		if(p->m_left != NULL)
			Q.EnQueue(p->m_left);
		if(p->m_right != NULL)
			Q.EnQueue(p->m_right);
	}
}

int Tree::Height(Node *root)
{
	int i = 0;
	Node *p = root;
	SeqQueue<Node*> Q;
	Q.EnQueue(p);
	while(!Q.IsEmpty())
	{
		int len = Q.getSize();
		++i;
		while(len--)
		{
			Q.DeQueue(p);
			if(p->m_left != NULL)
				Q.EnQueue(p->m_left);
			if(p->m_right != NULL)
				Q.EnQueue(p->m_right);
		}
	}
	return i;

}
void Tree::InThread(Node *&root,Node *&pre)
{
	if(root == NULL)
		return;
	InThread(root->m_left,pre);
	if(root->m_left == NULL)
	{
		root->lflag = 1;
		root->m_left = pre;
	}
	if(pre != NULL && pre->m_right == NULL)
	{
		pre->rflag = 1;
		pre->m_right = root;
	}
	pre = root;
	InThread(root->m_right,pre);
}
void Tree::PreThreadOrder(Node *root)
{
	Node *p = root;
	while(p)
	{
		cout<<p->m_value<<" ";
		if(p->lflag == 0) //有左子树
			p = p->m_left;
		else if(p->rflag == 0)//有右子树
			p = p->m_right;
		else  //没有左子树和右子树，找后继
		{
			while(p != NULL && p->rflag == 1)
				p = p->m_right;
			if(p != NULL)
				p = p->m_right;
		}

	}
}

 str代表的树是这样子的

 

 

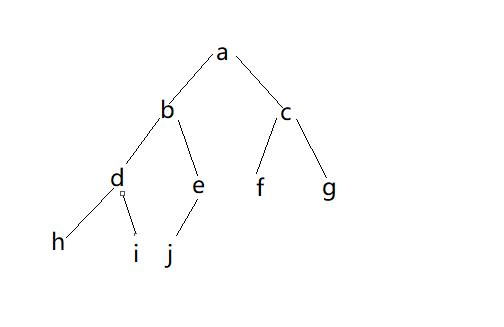
#include"header.h"
int main()
{
	char *str = "abdh##i##ej###cf##g##";
	Tree t('#');
	Node *p = NULL;
	t.m_root = t.create(str);
	t.PreOrder(t.m_root);
	cout<<endl;
	cout<<"Itera PreOrder: ";
	t.Itera_PreOrder(t.m_root);
	cout<<endl;
	t.inOrder(t.m_root);
	cout<<endl;
	t.postOrder(t.m_root);
	cout<<endl;
	t.levelOrder(t.m_root);
	cout<<endl;
	cout<<t<<endl;
	cout<<t.Height(t.m_root)<<endl;
	return 0;
}

 #代表指针为空，创建二叉树是使用的为前序

 

 这里主要讲一下使用迭代的前序遍历和层次遍历

迭代的前序遍历使用了栈，每次访问一个节点后，在向左子树遍历下去之前，利用这个栈记录该节点的右子女节点的地址，以便在左子树退回时可以直接从栈顶取得右子树的根节点，继续右子树的前序遍历。

 

 按层次顺序访问二叉树的处理需要利用一个队列。在访问二叉树的某一层结点时，把下一层指针预先入队，利用队列的先进先出特性安排层次访问的次序。因此，每当访问一个节点时，将它的子女按顺序加到队列的队尾，然后再访问已经在队列头部的结点，这样就可以实现二叉树的按层次访问。