统计数字问题
问题描述:一本书的页码从自然数1开始顺序编码直到自然数n。输的页码按照通常的习惯编排,每个页码都不含有多余的前导数字0.例如,第6页用数字6表示,而不是06或者006等。数字计数问题要求对给定书的总页码n,计算出书的全部页码中分别用到多少次数字0,1,2...8,9。
算法设计:给定表示书的总页码的十进制整数n(1<=n<=10^9),计算书的全部页码中分别用到多少次数字0,1,2...8,9。
数据输入:输入数据由文件名为input.txt的文本提供。每个文件只有1行,给出表示书的总页码的整数n。
结果输出:将计算结果输出到文件output.txt。输出文件总共10行,在第k行输出页码中用到数字k-1的次数,k=1,2,....,10。
输入文件示例
input.txt
11
输出文件示例
output.txt
1
4
1
1
1
1
1
1
1
1
我的思路特别简单,就是将页码数遍历一遍,每个页码计算其含有的数字,并将各个数值累加在一个全局数组中。
#include<iostream>
#include<string.h>
#include<unistd.h>
#include<fstream>
using namespace std;
#define INPUT_FILE "input.txt"
#define OUTPUT_FILE "output.txt"
int count[10] = {};
void input_book_num(char* file)
{
ofstream fp;
fp.open(file, ios::out);
if(!fp)
{
cerr<<"Open file failed."<<endl;
exit(1);
}
int a = 0;
cout<<"请输入书目页码:";
cin>>a;
fp<<a<<endl;
fp.close();
}
void output(char* file, int nu)//将计算好的数据放入output.txt文件
{
ofstream fp;
fp.open(file, ios::app);
if(!fp)
{
cerr<<"Open file"<<"\""<<file<<"\""<<"failed."<<endl;
exit(1);
}
fp<<nu<<endl;
fp.close();
}
void read(char* file, int *nu)//从input.txt中读取总页码
{
cout<<"书本页码读取中...."<<endl;
sleep(1);
ifstream fp;
fp.open(file, ios::in);
if(!fp)
{
cerr<<"Open file"<<"\""<<file<<"\""<<"failed."<<endl;
exit(1);
}
fp>>*nu;
fp.close();
}
void num_handling(int nu)
{
cout<<"结果计算中..."<<endl;
sleep(1);
int a = 0, c = 0;
while(nu)//对页码数进行遍历
{
a = nu;
while(a)
{
c = a%10;//得到个位数字
switch (c)
{
case 0:
++count[0];
break;
case 1:
++count[1];
break;
case 2:
++count[2];
break;
case 3:
++count[3];
break;
case 4:
++count[4];
break;
case 5:
++count[5];
break;
case 6:
++count[6];
break;
case 7:
++count[7];
break;
case 8:
++count[8];
break;
case 9:
++count[9];
break;
default:
break;
}
a = a/10;将页码数缩小十倍
}
--nu;
}
}
int main()
{
int nu = 0;
int *pnu = ν
input_book_num(INPUT_FILE);
read(INPUT_FILE, pnu);
cout<<"nu = "<<nu<<endl;
num_handling(nu);
cout<<"将结果写入"<<OUTPUT_FILE<<"文件中...."<<endl;
for(int i=0; i<10; ++i)
{
output(OUTPUT_FILE, count[i]);
}
return 0;
}
计算结果
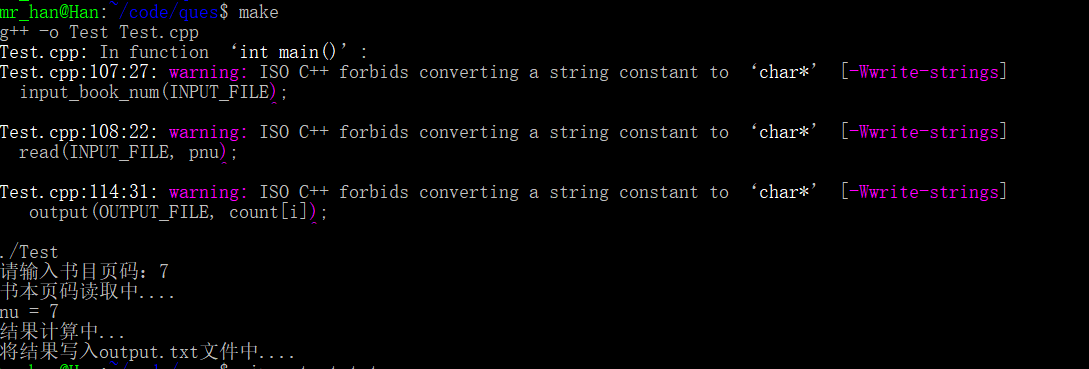
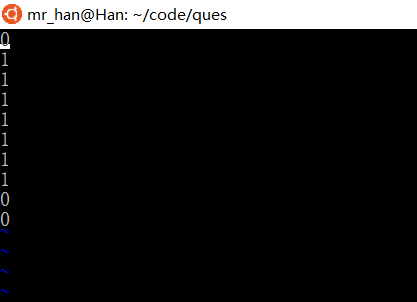
output.txt
测试用例试试
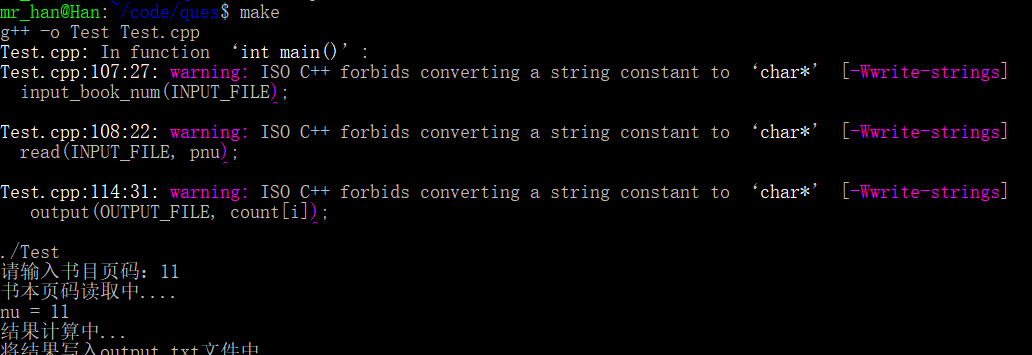
output.txt

再试个大的
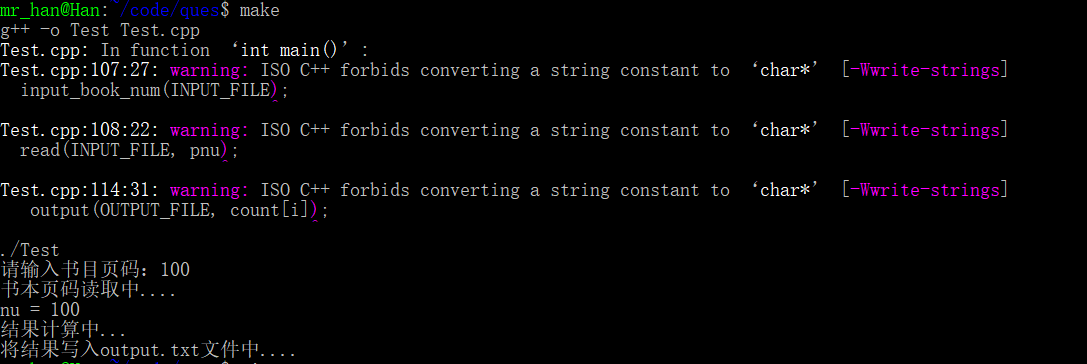
output.txt

1000试试

结果这么有规律,应该没问题。
vim文件清空命令
在第一行用dG然后wq回车退出即可。
不积小流无以成江河




