对称加密-流加密-祖冲之算法(ZUC)
祖冲之加密算法(ZUC)是我国自主设计的流密码算法,主要用于与4G网络中的加密,目前主要应用在通信领域当中。
祖冲之算法的执行流程如下图所示。

祖冲之算法由三部分组成,线性反馈移位寄存器(LFSR),比特重组(BR)和非线性函数(F)。算法结构图如下图所示。
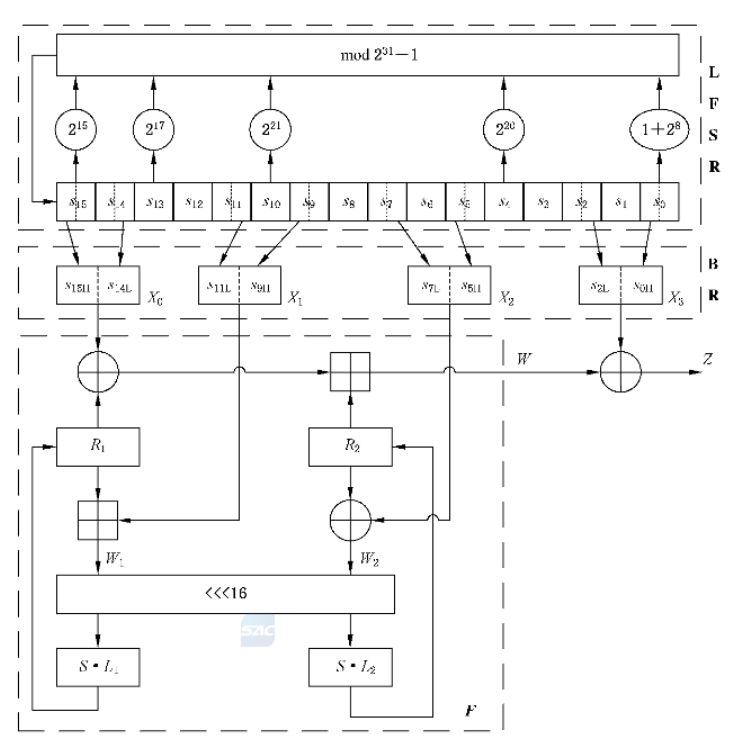
线性反馈移位寄存器(LFSR)
LFSR包括16个31比特寄存器单元S0 ~ S15。LFSR的运行模式有两种:初始化模式和工作模式。
初始化模式:

工作模式:

比特重组(BR)

非线性函数(F)

密钥装入:

实现代码:
#include<iostream> #include<array> #include<string> using namespace std; const unsigned char S0[256] = { 0x3e, 0x72, 0x5b, 0x47, 0xca, 0xe0, 0x00, 0x33, 0x04, 0xd1, 0x54, 0x98, 0x09, 0xb9, 0x6d, 0xcb, 0x7b, 0x1b, 0xf9, 0x32, 0xaf, 0x9d, 0x6a, 0xa5, 0xb8, 0x2d, 0xfc, 0x1d, 0x08, 0x53, 0x03, 0x90, 0x4d, 0x4e, 0x84, 0x99, 0xe4, 0xce, 0xd9, 0x91, 0xdd, 0xb6, 0x85, 0x48, 0x8b, 0x29, 0x6e, 0xac, 0xcd, 0xc1, 0xf8, 0x1e, 0x73, 0x43, 0x69, 0xc6, 0xb5, 0xbd, 0xfd, 0x39, 0x63, 0x20, 0xd4, 0x38, 0x76, 0x7d, 0xb2, 0xa7, 0xcf, 0xed, 0x57, 0xc5, 0xf3, 0x2c, 0xbb, 0x14, 0x21, 0x06, 0x55, 0x9b, 0xe3, 0xef, 0x5e, 0x31, 0x4f, 0x7f, 0x5a, 0xa4, 0x0d, 0x82, 0x51, 0x49, 0x5f, 0xba, 0x58, 0x1c, 0x4a, 0x16, 0xd5, 0x17, 0xa8, 0x92, 0x24, 0x1f, 0x8c, 0xff, 0xd8, 0xae, 0x2e, 0x01, 0xd3, 0xad, 0x3b, 0x4b, 0xda, 0x46, 0xeb, 0xc9, 0xde, 0x9a, 0x8f, 0x87, 0xd7, 0x3a, 0x80, 0x6f, 0x2f, 0xc8, 0xb1, 0xb4, 0x37, 0xf7, 0x0a, 0x22, 0x13, 0x28, 0x7c, 0xcc, 0x3c, 0x89, 0xc7, 0xc3, 0x96, 0x56, 0x07, 0xbf, 0x7e, 0xf0, 0x0b, 0x2b, 0x97, 0x52, 0x35, 0x41, 0x79, 0x61, 0xa6, 0x4c, 0x10, 0xfe, 0xbc, 0x26, 0x95, 0x88, 0x8a, 0xb0, 0xa3, 0xfb, 0xc0, 0x18, 0x94, 0xf2, 0xe1, 0xe5, 0xe9, 0x5d, 0xd0, 0xdc, 0x11, 0x66, 0x64, 0x5c, 0xec, 0x59, 0x42, 0x75, 0x12, 0xf5, 0x74, 0x9c, 0xaa, 0x23, 0x0e, 0x86, 0xab, 0xbe, 0x2a, 0x02, 0xe7, 0x67, 0xe6, 0x44, 0xa2, 0x6c, 0xc2, 0x93, 0x9f, 0xf1, 0xf6, 0xfa, 0x36, 0xd2, 0x50, 0x68, 0x9e, 0x62, 0x71, 0x15, 0x3d, 0xd6, 0x40, 0xc4, 0xe2, 0x0f, 0x8e, 0x83, 0x77, 0x6b, 0x25, 0x05, 0x3f, 0x0c, 0x30, 0xea, 0x70, 0xb7, 0xa1, 0xe8, 0xa9, 0x65, 0x8d, 0x27, 0x1a, 0xdb, 0x81, 0xb3, 0xa0, 0xf4, 0x45, 0x7a, 0x19, 0xdf, 0xee, 0x78, 0x34, 0x60}; const unsigned char S1[256] = { 0x55, 0xc2, 0x63, 0x71, 0x3b, 0xc8, 0x47, 0x86, 0x9f, 0x3c, 0xda, 0x5b, 0x29, 0xaa, 0xfd, 0x77, 0x8c, 0xc5, 0x94, 0x0c, 0xa6, 0x1a, 0x13, 0x00, 0xe3, 0xa8, 0x16, 0x72, 0x40, 0xf9, 0xf8, 0x42, 0x44, 0x26, 0x68, 0x96, 0x81, 0xd9, 0x45, 0x3e, 0x10, 0x76, 0xc6, 0xa7, 0x8b, 0x39, 0x43, 0xe1, 0x3a, 0xb5, 0x56, 0x2a, 0xc0, 0x6d, 0xb3, 0x05, 0x22, 0x66, 0xbf, 0xdc, 0x0b, 0xfa, 0x62, 0x48, 0xdd, 0x20, 0x11, 0x06, 0x36, 0xc9, 0xc1, 0xcf, 0xf6, 0x27, 0x52, 0xbb, 0x69, 0xf5, 0xd4, 0x87, 0x7f, 0x84, 0x4c, 0xd2, 0x9c, 0x57, 0xa4, 0xbc, 0x4f, 0x9a, 0xdf, 0xfe, 0xd6, 0x8d, 0x7a, 0xeb, 0x2b, 0x53, 0xd8, 0x5c, 0xa1, 0x14, 0x17, 0xfb, 0x23, 0xd5, 0x7d, 0x30, 0x67, 0x73, 0x08, 0x09, 0xee, 0xb7, 0x70, 0x3f, 0x61, 0xb2, 0x19, 0x8e, 0x4e, 0xe5, 0x4b, 0x93, 0x8f, 0x5d, 0xdb, 0xa9, 0xad, 0xf1, 0xae, 0x2e, 0xcb, 0x0d, 0xfc, 0xf4, 0x2d, 0x46, 0x6e, 0x1d, 0x97, 0xe8, 0xd1, 0xe9, 0x4d, 0x37, 0xa5, 0x75, 0x5e, 0x83, 0x9e, 0xab, 0x82, 0x9d, 0xb9, 0x1c, 0xe0, 0xcd, 0x49, 0x89, 0x01, 0xb6, 0xbd, 0x58, 0x24, 0xa2, 0x5f, 0x38, 0x78, 0x99, 0x15, 0x90, 0x50, 0xb8, 0x95, 0xe4, 0xd0, 0x91, 0xc7, 0xce, 0xed, 0x0f, 0xb4, 0x6f, 0xa0, 0xcc, 0xf0, 0x02, 0x4a, 0x79, 0xc3, 0xde, 0xa3, 0xef, 0xea, 0x51, 0xe6, 0x6b, 0x18, 0xec, 0x1b, 0x2c, 0x80, 0xf7, 0x74, 0xe7, 0xff, 0x21, 0x5a, 0x6a, 0x54, 0x1e, 0x41, 0x31, 0x92, 0x35, 0xc4, 0x33, 0x07, 0x0a, 0xba, 0x7e, 0x0e, 0x34, 0x88, 0xb1, 0x98, 0x7c, 0xf3, 0x3d, 0x60, 0x6c, 0x7b, 0xca, 0xd3, 0x1f, 0x32, 0x65, 0x04, 0x28, 0x64, 0xbe, 0x85, 0x9b, 0x2f, 0x59, 0x8a, 0xd7, 0xb0, 0x25, 0xac, 0xaf, 0x12, 0x03, 0xe2, 0xf2}; const unsigned int d[16] = { 0x44d7, 0x26bc, 0x626b, 0x135e, 0x5789, 0x35e2, 0x7135, 0x09af, 0x4d78, 0x2f13, 0x6bc4, 0x1af1, 0x5e26, 0x3c4d, 0x789a, 0x47ac}; //模2^31 - 1加法 unsigned int mod_add(unsigned int a, unsigned int b){ unsigned int c = a + b; c = (c & 0x7fffffff) + (c >> 31); return c; } //模2^31 - 1乘法 unsigned int mod_mul(unsigned int a, int exp){ return (a << exp) | (a >> (31 - exp)); } //实现循环左移的功能 unsigned int rol(unsigned int val, int size) { unsigned res = val << size; res |= val >> (32 - size); return res; } array<unsigned int, 17> LFSR_s {}; array<unsigned int, 4> X {}; unsigned int R1 = 0, R2 = 0, W = 0; /*=================== LFSR的初始化模式 ======================*/ void LFSRWithInitialisationMode(unsigned int u){ unsigned int v, temp; v = LFSR_s[0]; temp = mod_mul(LFSR_s[0], 8); v = mod_add(v, temp); temp = mod_mul(LFSR_s[4], 20); v = mod_add(v, temp); temp = mod_mul(LFSR_s[10], 21); v = mod_add(v, temp); temp = mod_mul(LFSR_s[13], 17); v = mod_add(v, temp); temp = mod_mul(LFSR_s[15], 15); v = mod_add(v, temp); LFSR_s[16] = mod_add(v, u); if(LFSR_s[16] == 0) LFSR_s[16] = 0x7fffffff; for(int i = 0; i < 16; i++) LFSR_s[i] = LFSR_s[i + 1]; } /*=================== LFSR的工作模式 ======================*/ void LFSRWithWorkMode(){ unsigned int v, temp; v = LFSR_s[0]; temp = mod_mul(LFSR_s[0], 8); v = mod_add(v, temp); temp = mod_mul(LFSR_s[4], 20); v = mod_add(v, temp); temp = mod_mul(LFSR_s[10], 21); v = mod_add(v, temp); temp = mod_mul(LFSR_s[13], 17); v = mod_add(v, temp); temp = mod_mul(LFSR_s[15], 15); v = mod_add(v, temp); LFSR_s[16] = v; if(LFSR_s[16] == 0) LFSR_s[16] = 0x7fffffff; for(int i = 0; i < 16; i++) LFSR_s[i] = LFSR_s[i + 1]; } /*======================= 比特重组BR ======================*/ void BitReconstruction(){ X[0] = ((LFSR_s[15] & 0x7fff8000) << 1) | (LFSR_s[14] & 0xffff); X[1] = (LFSR_s[11] << 16) | (LFSR_s[9] >> 15); X[2] = (LFSR_s[7] << 16) | (LFSR_s[5] >> 15); X[3] = (LFSR_s[2] << 16) | (LFSR_s[0] >> 15); } /*====================== 非线性函数F =====================*/ unsigned int L1(unsigned int a){ return a ^ rol(a, 2) ^ rol(a, 10) ^ rol(a, 18) ^ rol(a, 24); } unsigned int L2(unsigned int a){ return a ^ rol(a, 8) ^ rol(a, 14) ^ rol(a, 22) ^ rol(a, 30); } unsigned int S(unsigned int a){ unsigned char x[4] = {0}, y[4] = {0}; unsigned int b = 0; int i = 0; x[0] = a >> 24; x[1] = (a >> 16) & 0xff; x[2] = (a >> 8) & 0xff; x[3] = a & 0xff; for (i = 0; i < 4; i++){ if (i == 0 || i == 2) y[i] = S0[x[i]]; else y[i] = S1[x[i]]; } b = (y[0] << 24) | (y[1] << 16) | (y[2] << 8) | y[3]; return b; } void F(){ unsigned int W1 = 0, W2 = 0; //unsigned int tmp1 = 0, tmp2 = 0; W = (X[0] ^ R1) + R2; W1 = R1 + X[1]; W2 = R2 ^ X[2]; R1 = S(L1((W1 << 16) | (W2 >> 16))); R2 = S(L2((W2 << 16) | (W1 >> 16))); } /*========================== 实现密钥装入的功能 =============*/ void key_place(unsigned int *k, unsigned int *iv){ for (int i = 0; i < 16; i++) LFSR_s[i] = (k[i] << 23) | (d[i] << 8) | iv[i]; } int main(void){ unsigned int key[16] = {0}; unsigned int iv[16] = {0}; int L = 16; string Plaintext = "hello world! "; string Ciphertext; unsigned int *keystream = (unsigned int *)malloc(L * sizeof(unsigned int)); /*===================== 算法运行初始化步骤 ===================*/ key_place(key, iv); R1 = 0; R2 = 0; for(int i = 0; i < 32; i++){ BitReconstruction(); F(); LFSRWithInitialisationMode(W >> 1); } /*==================== 算法运行工作步骤 =======================*/ BitReconstruction(); F(); LFSRWithWorkMode(); for(int i = 0; i < L; i++){ BitReconstruction(); F(); keystream[i] = W ^ X[3]; LFSRWithInitialisationMode(W >> 1); } for(int i = 0; i < L; i++) cout << hex << keystream[i] << " "; cout << endl; cout << "Encryption: " << endl << "Ciphertext is: " ; for(int i = 0; i<Plaintext.length(); i++){ Ciphertext[i] = char(keystream[i] ^ (int)Plaintext[i]); cout << Ciphertext[i]; } Ciphertext[Plaintext.length()] = '\0'; cout << endl; cout << "Decryption: " << endl << "Plaintext is: " ; for(int i = 0; i<Plaintext.length(); i++){ cout << char(keystream[i] ^ (int)Ciphertext[i]); } free(keystream); keystream = NULL; return 0; }
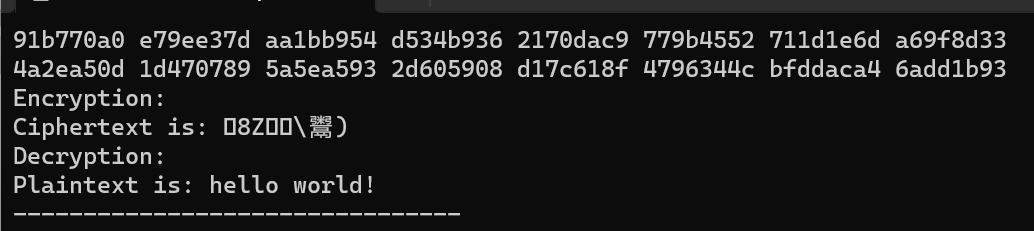
运行结果。
参考资料
[1] 信息安全技术 祖冲之序列密码算法(GB/T 33133.1 - 2016),中华人民共和国国家标准,http://c.gb688.cn/bzgk/gb/showGb?type=online&hcno=8C41A3AEECCA52B5C0011C8010CF0715
[2] 祖冲之算法(ZUC-128)C语言实现,CSDN,https://blog.csdn.net/qq_43094622/article/details/105823724


 浙公网安备 33010602011771号
浙公网安备 33010602011771号