python算法:握手问题
一，题目
小明在家中举办派对，请邀请好友来参加，
来参加宴会的每两个人之间要握手，而且是仅握手一次，
则当人数为n时总共需要握手多少次?
二，解析
1,思路：
我们假设每个人到达后按先后顺序握手:
这样从人数最少时开始分析:
开始时会场中只有小明，是参会的第一个人，
假设第二个人到达时，与小明握手1次，可得：f(2) = 1
第三个人到达时,与小明,第2握手各1次,可以得到:f(3) = 2
第四位客人到达时,与小明，第2，第3握手各1次,可以得到:f(4) = 3
以此类推：
第n个人到达时，与屋内的n-1个人都握手1次,可以得到 f(n) = n-1
我们要获取的就是这些握手次数加和
2,设计:
握手次数加和:
既可以循环累加，也可以使用递归：
有两个人时的握手次数:f(2) = 1
有3个人时的握手总次数:f(3) = f(2)+2
有4个人时的握手总次数:f(4) = f(3)+3
…
以此类推
有n个人时的握手总次数:f(n) = f(n-1)+n-1
由此可以得到方程式:
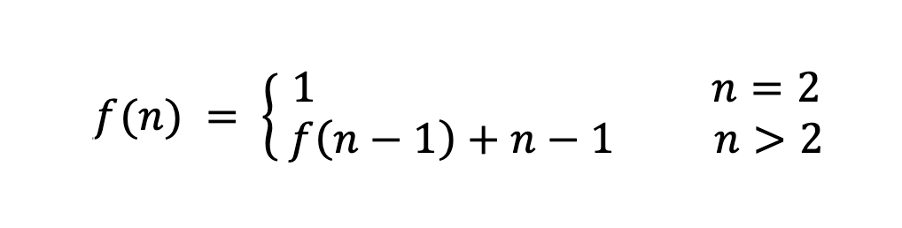
三，编写代码:
1,使用递归函数
|
1
2
3
4
5
6
7
8
9
10
11
|
# 函数,得到握手总次数# n: 参与握手的人数def shake(n): if n <= 1: return 0 elif n == 2: return 1 else: return shake(n-1)+n-1n = 12print(f"{n}个人共需握手{shake(n)}次") |
运行结果:
12个人共需握手66次2,使用循环
|
1
2
3
4
5
6
7
8
9
10
|
# 函数,得到握手总次数# n: 参与握手的人数def shake(n): total = 0 # 初始化总次数 for s in range(2, n + 1): # 人数的范围:从2到n num = s-1 # 当前人数的握手次数 total += num # 加到总次数中 return totaln = 12print(f"{n}个人共需握手{shake(n)}次") |
运行结果:
12个人共需握手66次