python算法:借书方案

一，for循环:

1,功能：重复执行同一段代码
语法:

for index in range(n): 
    # 循环体代码

index : 用来依次接收可迭代对象中的元素的变量名
range()函数:负责返回整数序列

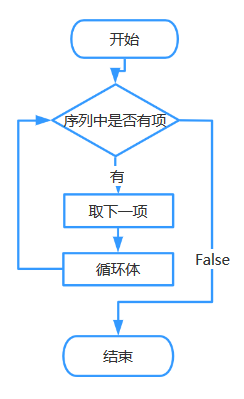
流程图:

2,应用

range可以同时指定start 和stop,用for遍历并打印

# 指定 start和stop
# print的参数 end=" " 用来使打印不换行
for num in range(3,9):
    print(num, end=" ")

运行结果:

3 4 5 6 7 8

说明：刘宏缔的架构森林—专注it技术的博客，
网址：https://imgtouch.com
本文: https://blog.imgtouch.com/index.php/2024/03/22/python-suan-fa-jie-shu-fang-an/
代码: https://github.com/liuhongdi/ 或 https://gitee.com/liuhongdi
说明：作者:刘宏缔邮箱: 371125307@qq.com

二，借书方案的题目与解析

1,题目：

小明有5本新书，要借给A、B、C三位小朋友，
若每人每次只能借1本，则可以有多少种不同的借法？

2,解析:

思路：
本题属于数学中常见的排列组合问题，即求从5个数中取3个不同数的排列组合的总数,
第一个人取时有5种选择，
第二个人取时有4种选择(第一个人已选走了一本)，
第三个人取时有3种选择(前两个人已选走了两本)，
所以预计有5x4x3=60种分法

用程序处理时:
1,对于每个人所选书号，我们可以采用循环实现，
即从每个人可选书号（1、2、3、4、5）的范围内进行穷举。
第一个人的选择，可以用循环将其列出，即for a in range(1,6)。
同理，对于第二个人、第三个人可以用同样的方法。
2,因为一本书只能借给一个人，所以第二个人的选择会受到第一个人的限制，
最后一个人的选择会受到前两个人的限制，
即后面的选择都是在前面选择的前提下进行的，
所以需要采用循环的嵌套来解决问题。
3,因为要保证三个人所选书号各不相同，
所以需要用 “if a != b and a != c and c != b”进行判断

三，编写代码:

# A、B、C三位小朋友，5本书，每人每次只能借一本
# 用a、b、c分别表示三人所选图书的编号
count = 0  # count表示有效借阅次数
# a表示A借阅图书的编号
for a in range(1, 6):
    # b表示B借阅图书的编号
    for b in range(1, 6):
        # c表示C借阅图书的编号
        for c in range(1, 6):
            if a != b and a != c and c != b:     # 三个人借的书必须编号不同
                print(f"A:{a} B:{b} C:{c}   ", end='')
                count += 1     # 借阅方法加1
                if count % 6 == 0:    # 每6个方法打印一个换行符
                    print()  # 换行
print(f"共有{count}种有效借阅方法")

运行结果:

A:1 B:2 C:3   A:1 B:2 C:4   A:1 B:2 C:5   A:1 B:3 C:2   A:1 B:3 C:4   A:1 B:3 C:5   
A:1 B:4 C:2   A:1 B:4 C:3   A:1 B:4 C:5   A:1 B:5 C:2   A:1 B:5 C:3   A:1 B:5 C:4   
A:2 B:1 C:3   A:2 B:1 C:4   A:2 B:1 C:5   A:2 B:3 C:1   A:2 B:3 C:4   A:2 B:3 C:5   
A:2 B:4 C:1   A:2 B:4 C:3   A:2 B:4 C:5   A:2 B:5 C:1   A:2 B:5 C:3   A:2 B:5 C:4   
A:3 B:1 C:2   A:3 B:1 C:4   A:3 B:1 C:5   A:3 B:2 C:1   A:3 B:2 C:4   A:3 B:2 C:5   
A:3 B:4 C:1   A:3 B:4 C:2   A:3 B:4 C:5   A:3 B:5 C:1   A:3 B:5 C:2   A:3 B:5 C:4   
A:4 B:1 C:2   A:4 B:1 C:3   A:4 B:1 C:5   A:4 B:2 C:1   A:4 B:2 C:3   A:4 B:2 C:5   
A:4 B:3 C:1   A:4 B:3 C:2   A:4 B:3 C:5   A:4 B:5 C:1   A:4 B:5 C:2   A:4 B:5 C:3   
A:5 B:1 C:2   A:5 B:1 C:3   A:5 B:1 C:4   A:5 B:2 C:1   A:5 B:2 C:3   A:5 B:2 C:4   
A:5 B:3 C:1   A:5 B:3 C:2   A:5 B:3 C:4   A:5 B:4 C:1   A:5 B:4 C:2   A:5 B:4 C:3   
共有60种有效借阅方法

一，for循环:

二，借书方案的题目与解析

三，编写代码:

公告