python: 递归函数：汉诺塔

一，认识递归函数

1，什么是递归?
递归的工作原理是，如果函数需要处理的问题大小合适，则直接求解并返回结果，
否则将问题分解成两个或多个更小的子问题，并对子问题进行相同的处理，
直到问题无法分解为止

2,什么是递归函数:
递归函数（recursive function）是指在函数体中可以调用自己的函数

3,语法

def fn():
    # ...
    if condition:
        # 停止自我调用
    else:
        fn()
    # ...

4,递归函数的优点和缺点

递归函数的优点:它们可以帮助程序员在处理复杂问题时提供一种简单且易懂的解决方案。
递归函数使代码具有可读性和可重用性，
而且可以使用递归函数解决使用其他方法难以处理的问题。
递归函数的缺点: 递归函数可能会在运行时占用较多的系统资源，
因为它们需要在堆栈上存储多个函数调用
其次，递归函数可能导致代码变得不容易理解，
因为它具有一定的复杂度

二，汉诺塔

1,汉诺塔问题

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

我们编写代码时要遵循汉诺塔的规则: 小圆盘上不能放大圆盘，即大的圆盘不能放在小的圆盘上面
2, 先归纳最简单的情况:1个圆盘
如果A柱上只有一个圆盘，
那么移动圆盘的步骤显然是从A移动到C，即表示成 A–>C：

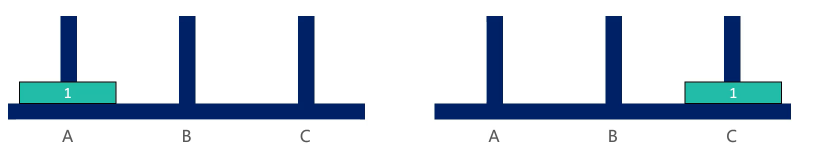
3, 如果A柱上有两片圆盘，也很容易想到只要3步就可以完成，
即
第1步：A上第一块–>B
第2步：A上第二块–>C
第3步：B上第一块–>C：

4,3个圆盘:

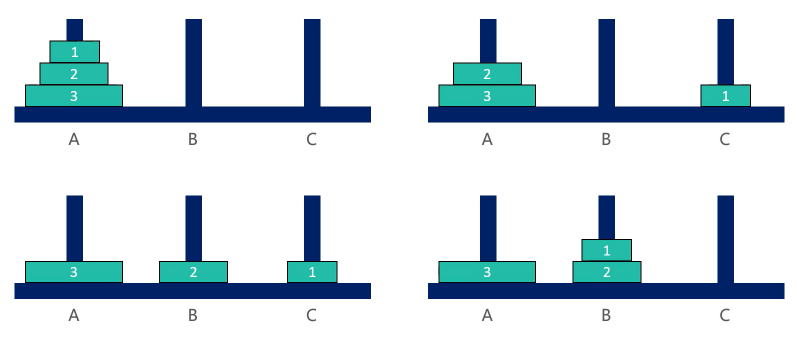
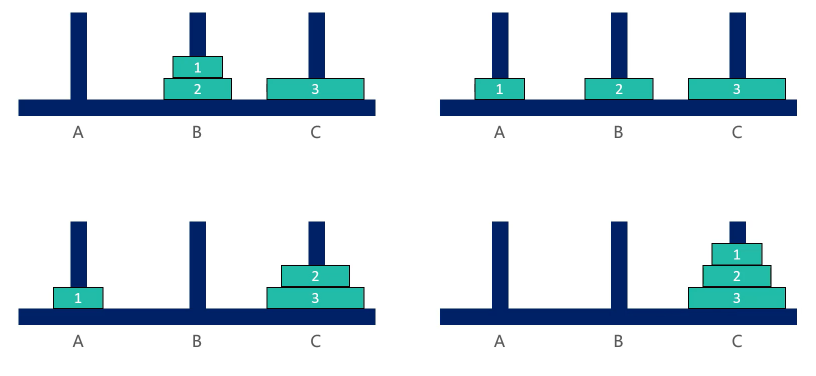
5,总结规律

总结规律即:
将A上面的n-1个圆盘，从A借助C移动到B：

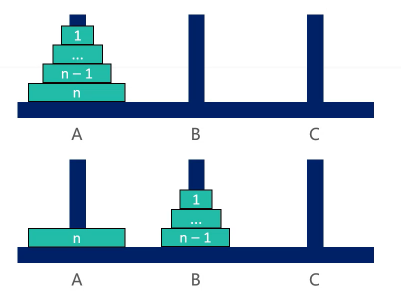
将A上最下面的一个圆盘，从A移动到C：

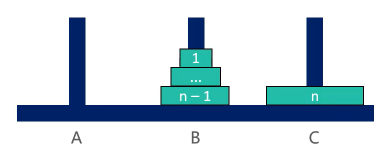
将B上面的n-1个圆盘，从B借助A移动到C：

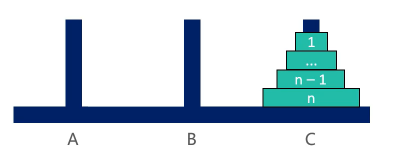
三，用程序解决汉诺塔

我们根据得到的规律，用递归的方式编写代码:

# n: 共几块
# a: 源
# b:辅助
# c:目标
 
def hanoi(n, a, b, c):
    if n == 1:
        print("{}:{}->{}".format(1, a, c))
    else:
        hanoi(n - 1, a, c, b)
        print("{}:{}->{}".format(n, a, c))
        hanoi(n - 1, b, a, c)
 
 
hanoi(2, "A", "B", "C")

运行结果:

1:A->B
2:A->C
1:B->C

如果是3块圆盘:

def hanoi(n, a, b, c):
    if n == 1:
        print("{}:{}->{}".format(1, a, c))
    else:
        hanoi(n - 1, a, c, b)
        print("{}:{}->{}".format(n, a, c))
        hanoi(n - 1, b, a, c)
 
 
hanoi(3, "A", "B", "C")

运行结果:

1:A->C
2:A->B
1:C->B
3:A->C
1:B->A
2:B->C
1:A->C

一，认识递归函数

二，汉诺塔

三，用程序解决汉诺塔

公告