OO第一次博客作业
OO第一次博客作业
三次编程作业:多项式求导,多项式+三角函数求导,求导支持表达式嵌套
(1) 基于度量来分析自己的程序结构
作业分析
第一次作业
任务为简单多项式导函数的求解。
解决方案:使用HashMap存储指数和系数
下图是IDEA生成的类图,可以看到本次作业只使用了2个类,Main类用于判断输入合法性以及调用Poly的方法构建一个表达式,Poly则是构建的表达式类,里边包含一个HashMap<BigInteger,BigInteger>用于表达一个表达式,同时也放了另一个Hashmap存储了求导之后的结果,public void parsePoly(String s, char op) 函数用于解析一个String里边的所有的项并加入Hashmap, public void diffe()用于表达式求导,public String toString() 用于表达式输出。
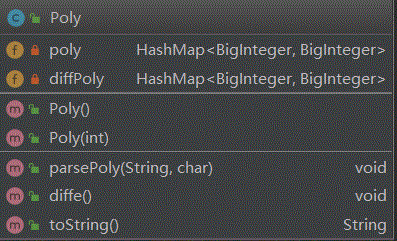
代码复杂度分析如下
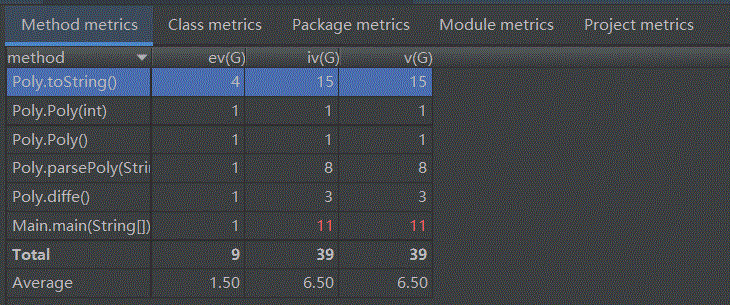
长度优化方法:主要涉及的就是-号开头的表达式,可以把后边的+提前就可以省略+,这样就节约了1个长度单位。
优点:初步学会了“面向对象”思维,HashMap的使用使得表达式的合并同类项等操作非常便捷。
缺点:一个Poly类中放置了2个HashMap对象分别保存求导前的表达式和求导后的表达式,这样一来toString方法中就限定了输出diffPloy对象,耦合度高。
修改:可以Poly类中只放置一个HashMap对象代表一个表达式,而求导后的表达式仍旧是一个表达式对象,可以new Poly()去实现。这样一来toString()方法就只是用来输出表达式了,而不是确定的输出“求导后的表达式”。
第二次作业
任务为包含简单幂函数和简单正余弦函数的导函数的求解。
解决方案:为了处理sin(x)和cos(x)同时为了一定程度上兼容下一次作业,设计一个Func因子类,存储了内外层函数,(虽然第三次作业没用上),同时表达式类Exp中使用了HashMap<HashMap<Func,BigInteger>, BigInteger> map; 这样的形式来表达了一个表达式,外层HashMap的value是系数(常数因子),key代表一个除去了常数因子的项,也就是sin(x),cos(x)和x三个基本函数的乘积,所以外层HashMap的key-value键值对表示一个完整的项;而内层HashMap的value是阶数,key是函数(x,sin(x),cos(x)),所以每个key-value键值对是一个因子,整个内层HashMap则表示了三类因子(x,sin(x),cos(x))的乘积。举例:sin(x)^2 + 4*x^3*cos(x) 我会将之表达为:{{x=3, cos(x)=1}=4, {sin(x)=2}=1}的形式。形式比较繁琐。
下图是IDEA生成的类图,可以看到本次作业使用了3个类,Main类用于判断输入合法性以及调用Poly的方法构建一个表达式,Exp则是构建的表达式类,Func则是因子类。
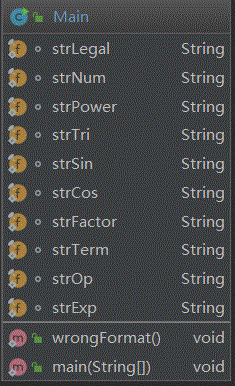
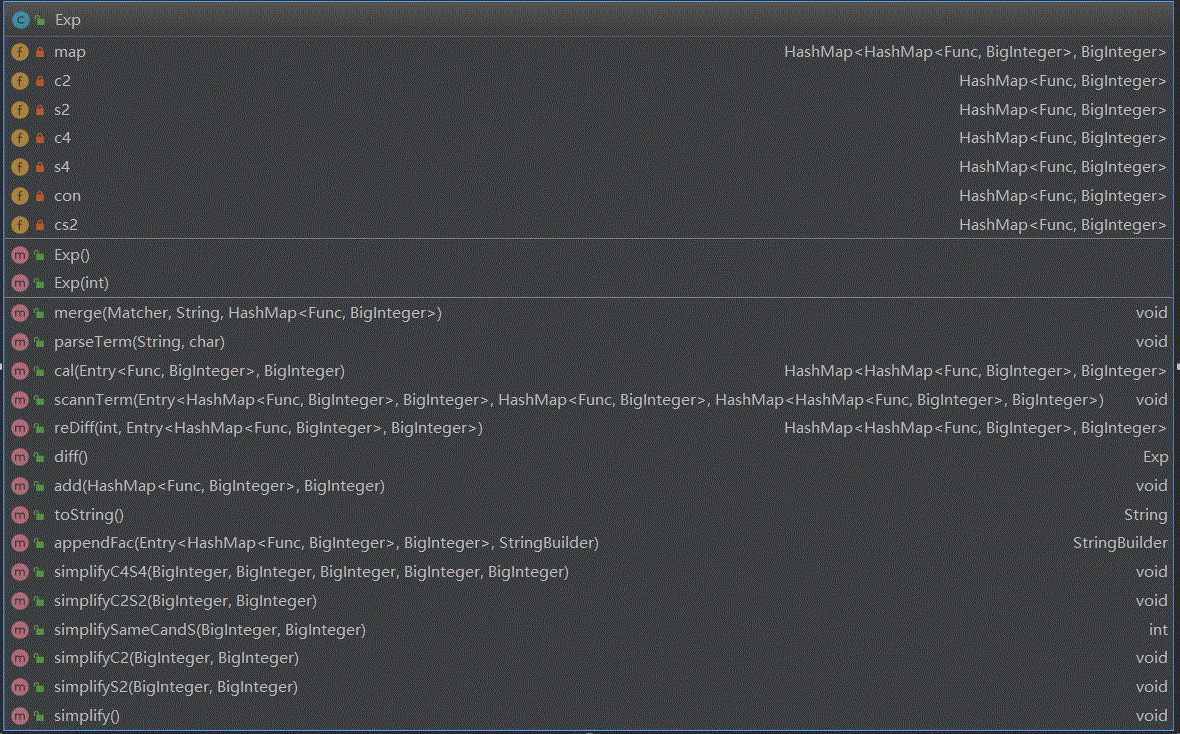
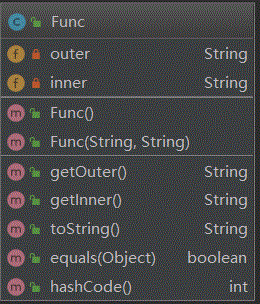
代码复杂度分析如下
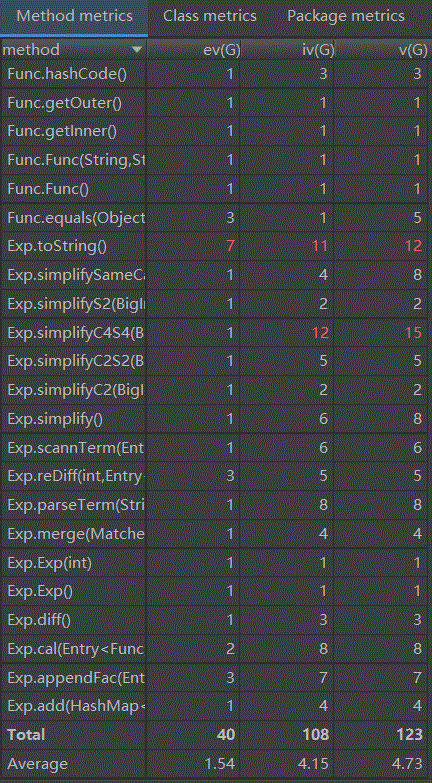
长度优化方法:public void simplify()函数。核心优化是sin(x)^2 + cos(x)^2=1,同时也优化了例如 sin(x)^2 - cos(x)^2 = 1 - 2*sin(x)^2 ; sin(x)^4 - cos(x)^4 = sin(x)^2 - cos(x)^2 = 1 - 2*sin(x)^2; sin(x)^4+ 2*sin(x)^2 *cos(x)^2 + cos(x)^4 = 1等方面。可以看出只是做了基于固定规则的简单优化,只处理了sin(x)|cos(x)的2次方,4次方的相关内容。同时由于架构问题,优化函数写的也比较复杂。
优点:OO度量的结果比之前更好,建立了因子类可以实现2层的嵌套。
缺点:采用了嵌套的HashMap结构导致表达式的形式较为复杂,对于“什么是表达式”,“什么是项”,“什么是因子”这样的整体架构理解不清晰。结构比较混乱,同时优化比较困难,只进行了一部分简单的优化。假想出来的第三次作业的架构,添加的Func类并没有实质的作用,嵌套HashMap反而造成麻烦,这个架构在第三次作业中还是需要推到重来。
修改:可以写一个A类,里边包含了cos(x),sin(x)和x各自的阶数,这个类就代表一个各项因子的乘积,采用一个HashMap<A,BigInteger>的形式,BigInteger代表这一项的系数(也就是常数因子),这样一个键值对就是一个项,整个HashMap就是表达式了。所有的形式都是用三元组表示的,这样求导变得比较简单,同时合并同类项也更加容易,只要基于A类相同就可以进行合并,或者说在HashMap插入过程中就可以直接合并同类项,便于长度的优化。(重写A类的hashcode()和equals()方法即可)。
第三次作业
任务为包含简单幂函数和简单正余弦函数的导函数的求解。支持嵌套因子和表达式因子。
解决方案:合法性判别:每次扫描表达式,将嵌套和表达式因子“抹去”,剩余的部分则变成了第2次作业的“表达式”,判断它是否合法;接着采用递归的方式去依次判别刚才“抹去”的部分是否符合表达式的定义(仍旧是递归判别)。求导:定义各种因子类和组合规则类,并且都实现了求导接口,接着对表达式求导也就是对因子和组合规则求导,主要采用了递归的方式。
下图是IDEA生成的类图,
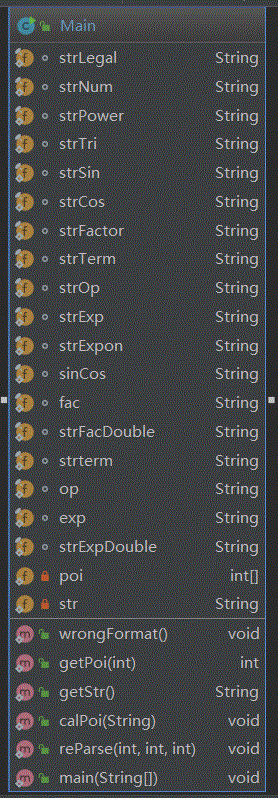
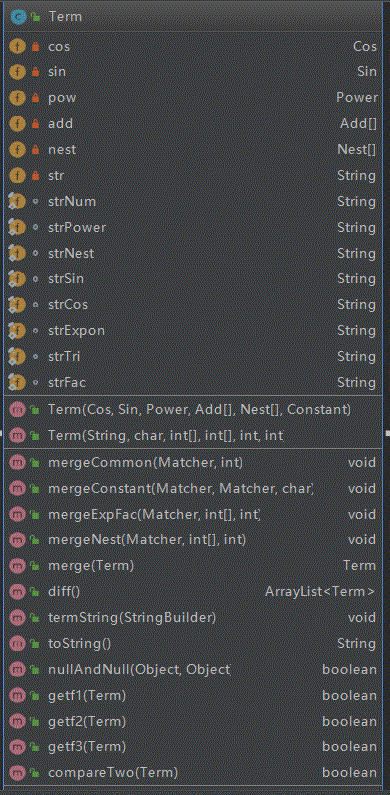
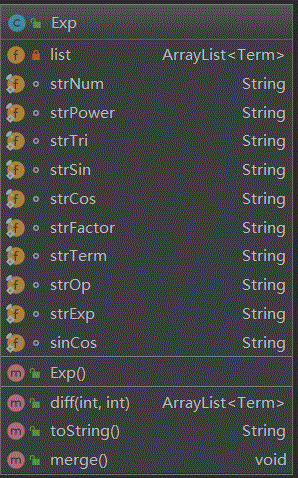
除此之外还有表示cos函数的Cos类,表示sin函数的Sin类,表示幂函数的Power类,表示常数的Constant类,表示表达式因子的Add类,表示嵌套因子的Nest类。
可以看出,Main类存储了str即合法的表达式字符串,public static void reParse(int l,int r,int kind)函数主要用于判断表达式是否合法,为了匹配括号的位置,首先要采用public static void calPoi(String str)函数中利用堆栈去记录了匹配的括号的位置,存储在poi[]数组之中。接着Exp类存储着一个ArrayList <Term>,也就是表达式是项的ArrayList,定义了public ArrayList<Term> diff(int l,int r)求导方法用于表达式求导,public String toString() 用于表达式输出,public void merge()用于同类项合并。而Term类中存放了一系列因子类的对象,用来表达一个项中包含哪些因子,通过public Term(String str,char op,int[] expfac,int[] sincos,int ef,int sc)可以解析出一个字符串(项)中所有的因子,构造这个项,public ArrayList<Term> diff()函数用于项的求导,public String toString()用于项的输出,public boolean compareTwo(Term t) 用于比较两个项之间能否合并同类项,public Term merge(Term t)用于项之间的合并。其他6个因子类中也都各自定义了求导方法,输出方法和比较是否相同的方法。
代码复杂度分析如下
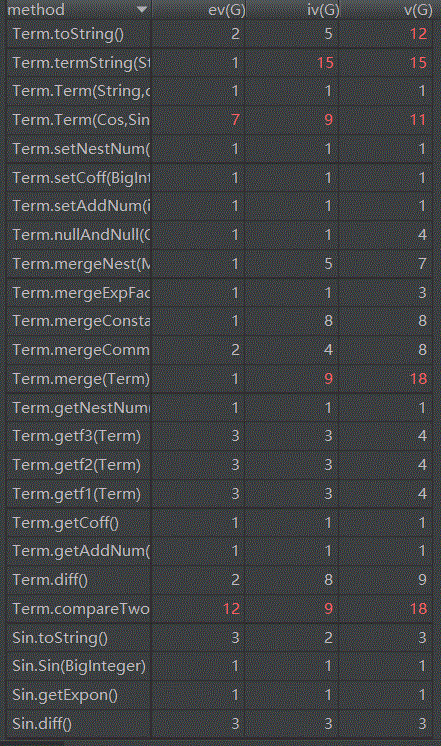
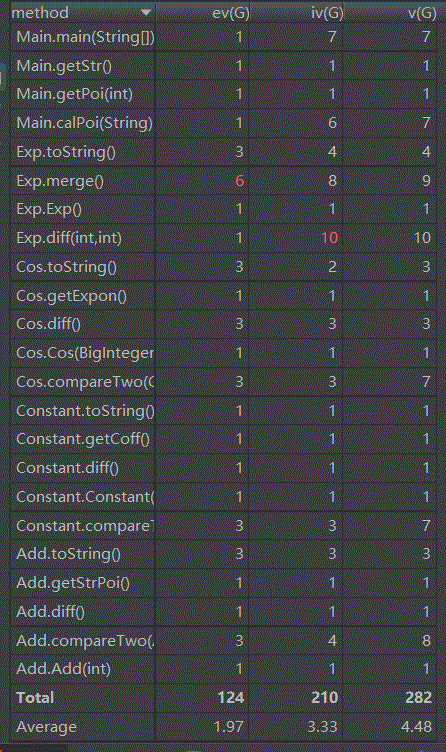
长度优化方法:(1)主要通过Exp类的merge方法,采用2重循环遍历所有的项,将能够合并的项进行合并。判断2个项之间能否合并采用的是Term类的compareTwo方法,它会一次比较项中的因子是否相同,进而得到项是否相同(只有常数因子不同)。(2)某些简单情况的长度优化:优化了表达式因子和嵌套因子中可能出现的无用的括号,例如sin(((((x)))))->cos(x)。
优点:OO度量再次下降。采用了先匹配对应的括号并记录下位置,再去利用正则表达式验证输入表达式的合法性的方式,解决了正则表达式无法匹配到对应括号的缺点,同时记录下来的对应括号位置信息在后边递归下降求导过程中也用到了。
缺点:没有很好的利用面向对象的方式,没有实现接口或继承。但实际上6个因子类可以实现一个接口(包含求导,输出,相互比较等方法),或者实现一个共同父类Factor。由于没有这样的实现,导致了我的Term类里放置了6种类的对象,十分混乱,同时嵌套因子类和表达式因子类由于一个项中可能出现多个,我才用了数组的方式进行存储,这样就导致了一些麻烦,需要记录下元素的个数,而且乘积求导时需要“你导我不导”时就会造成麻烦,不能很方便的实现插入删除操作,这个问题导致了后期debug比较困难,由此可见还是应该使用容器来存储。长度优化比较粗糙。
修改:对6个因子类实现一个公共父类,同时Term类只需要在放一个ArrayList<Factor>即可,不需要放置6种不同的类,这样一来操作比较方便,或者只是对嵌套因子类和表达式因子类的存放做出改变,采用ArrayLsit替代数组,可以减小编程难度。
(2) 分析自己程序的bug
三次中测以及强测均未发现bug。
三次互测中唯一发现了bug的在第三次。
这次的bug很不应该,虽然强测没有测出,但是可以看出本次的问题还是比较严重的。
首先,三次作业之中我所采用的策略均是讲一个表达式看做“[+-] 项+op+项+op+…+op+项”
那么我在处理表达式的时候,会使用正则去匹配到第一项,之后会利用循环使用正则匹配一个符号(+-),在匹配一个项。后边op+Term形式是固定的,唯一不同的就在于第一项,他的前边可以有一个[+-]符号,(这里所说的都是已经进行过判断WF,而格式正确的String)所以我会考察第一项的begin()位置,如果在0号位置说明没有[+-]号,如果在1号位置则说明有一个[+-]号,不会在2及以后的位置出现。这样就可以构造一个项了。(正负号会影响项的常数因子的正负。)
由此,我第一次作业代码如下
Poly po = new Poly(2048);
if (maTerm.start() == 1) {
po.parsePoly(maTerm.group(), str.charAt(0));
}
else {
po.parsePoly(maTerm.group(), '+');
}
第二次作业代码如下
Exp t = new Exp(64);
Matcher maTerm = Pattern.compile(strTerm).matcher(str);
maTerm.find(); //first term
if (maTerm.start() == 1) {
t.parseTerm(maTerm.group(), str.charAt(0));
} else {
t.parseTerm(maTerm.group(), '+');
}
第三次作业代码如下
if (maTerm.find()) {
Term t = new Term(maTerm.group(),'+',expfac,sincos,ef,sc); }
list.addAll(t.diff());
}
看到这,你应该已经发现了,第三次作业之中我忽略了第一项前边的[+-]号,只是采用了“+”传入,所以对于第一项前边有‘-’的数据都会WA
bug修复后代码如下
if (maTerm.find()) {
Term t;
if (maTerm.start() == 1) {
t = new Term(maTerm.group(),sb.charAt(0),expfac,sincos,ef,sc); }
else { t = new Term(maTerm.group(),'+',expfac,sincos,ef,sc); }
list.addAll(t.diff());
}
总之,这次的bug主要在于自己的忽视,过分注重所谓的”递归下降“求导,而忽视了对表达式的处理。或者说这就是测试不全面不认真的下场。因为这个bug是很严重的,稍加测试肯定可以发现,如果有第一次作业那样不断测试的态度的话这次不会有这样的bug产生。
(3) 分析自己发现别人程序bug所采用的策略
互测和自行课下测试的方式
(半)自动化测试
(1)自动造数据:第一次作业结束之后,在讨论区学习到了import nl.flotsam.xeger.Xeger;利用这个包可以基于正则表达式随机生成数据,因此在第2,3次作业的课下和互测中使用了它。但是对于第3次作业由于正则表达式是无法嵌套的,所以只是使用固定了某些嵌套因子混入其中,例如嵌套因子``,这样造了一些数据进行了测试,但这也就导致了第3次测试的不全面,只是造了一些普通的数据,而没有注意到第一项前边有[+-]号的情形。造数据的不全面主要是由于我的产生测试数据的程序其实就是按照”逐项造数据“并用+-号连接的方式,直接就忽略的第一项前的[+-]号,而1,2次作业手造数据时也会考虑这种情况,但第3次忘记了。
import nl.flotsam.xeger.Xeger;
import java.io.FileOutputStream;
FileOutputStream fos = new FileOutputStream(filePath);
for (int i = 0;i<3000;i++) {
String result = "";
Xeger generator = new Xeger(regex);
for (int j = 0; j < 10; j++) {
result = result + generator.generate();
Random r = new Random(10);
if (j!=9){
if(r.nextInt()>5)
result+="+";
else
result+="-";
}
}
result+="\n";
fos.write(result.getBytes());
}
(2)手动造数据
这个过程主要是考虑到我写的造数据的代码并不会覆盖到所有情况而且产生的数据都是格式正确且没有空格的,所以需要手动构造数据进行测试,主要是构造一些WF的格式错误和一些边界数据条件进行测试。
(3)正确性验证:利用matlab和python的sympy库进行验证。(早期使用的matlab,但是发现当常数值较大时,matlab经常出现奇怪错误,后期改用python验证,速度也比matlab快了一些)
matlab代码简单示意
syms x
fid = fopen('E:\out.txt','w');
y1=...(原表达式)
y2=...(我的输出结果)
fprintf(fid,'%s\r\n',simplify(diff(y1) - y2);
python代码简单示意
from sympy import *
x = Symbol('x')
y1=...(原表达式)
y2=...(我的输出结果)
print("%s" % (simplify(diff(y1)-y2)))
由于不擅长脚本,所以我采用的是使用java语言,读取我的程序的输出myout.txt和我造的数据data.txt文件,然后输出类似上边所示的程序语句到一个文件之中,然后拷贝到matlab建立m文件或python建立.py文件之后再运行并查看结果。互测时将程序读取的文件改为采用互测对象程序的输出文件即可。
public static void main(String[] args) {
String filePath ="E:\\py.txt";
String s1 = "from sympy import *";
String s2 = "x = Symbol('x')";
String s3 = "fid = open('E:\\out.txt','w')";
try {
FileOutputStream fos = new FileOutputStream(filePath);
fos.write(s1.getBytes());
fos.write("\n".getBytes());
fos.write(s2.getBytes());
fos.write("\n".getBytes());
File file1 = new File("E:\\data.txt");//造的数据
InputStreamReader inputReader1 = new InputStreamReader(new FileInputStream(file1));
BufferedReader bf1 = new BufferedReader(inputReader1);
File file2 = new File("E:\\Saberout.txt");//互测对象Saber的输出
InputStreamReader inputReader2 = new InputStreamReader(new FileInputStream(file2));
BufferedReader bf2 = new BufferedReader(inputReader2);
String str1,str2;
while ((str2 = bf2.readLine()) != null) {
str1 = bf1.readLine();
str1 = str1.replaceAll("\\^","**");//python的^需要使用**代替
str2 = str2.replaceAll("\\^","**");
fos.write("y1=".getBytes());
fos.write(str1.getBytes());
fos.write("\n".getBytes());
fos.write("y2=".getBytes());
fos.write(str2.getBytes());
fos.write("\n".getBytes());
fos.write("print(\"%s\" % (simplify(diff(y1)-y2)))".getBytes());
fos.write("\n".getBytes());
}
} catch (Exception e){
System.exit(0);
}
}
该程序会产生可以运行的.py文件的代码方便进行验证。
互测中我首先会采用如上的自动化测试,如果bug较多就不会去阅读这个人的代码的具体内容了,相反对于bug较少的代码我会手动构造数据并且仔细研读代码,从代码逻辑和正则的使用等等角度去分析寻找bug,这就是我互测的方法。
(4) Applying Creational Pattern
第一次作业
表达式由项的HashMap构成,只有2个类,Main和Poly。项只是有2个BigInger构成。HashMap<BigInteger, BigInteger> poly,diffpoly
重构:可以Poly类中只放置一个HashMap对象代表一个表达式,而求导后的表达式仍旧是一个表达式对象,可以new Poly()去实现。这样一来toString()方法就只是用来输出表达式了,而不是确定的输出“求导后的表达式”。
第二次作业
三个类,Main,Exp,Func,表达式类Exp中使用了HashMap<HashMap<Func,BigInteger>, BigInteger> map; 这样的形式来表达了一个表达式。
重构:可以写一个A类,里边包含了cos(x),sin(x)和x各自的阶数,这个类就代表一个各项因子的乘积,采用一个HashMap<A,BigInteger>的形式,BigInteger代表这一项的系数(也就是常数因子),这样一个键值对就是一个项,整个HashMap就是表达式了。所有的形式都是用三元组表示的,这样求导变得比较简单,同时合并同类项也更加容易,只要基于A类相同就可以进行合并,或者说在HashMap插入过程中就可以直接合并同类项,便于长度的优化。(重写A类的hashcode()和equals()方法即可)。
第三次作业
9个类,Main,Exp,Term和6个因子类(cos,sin,constant,nest,add,power)。表达式由项构成,项由因子构成,整体是递归的结构。Exp类里边是ArrayList<Term>对象,Term类里是6个因子对象 private Cos cos;private Sin sin ; private Power pow;private Add[] add;private Nest[] nest; private Constant con;。
重构:对6个因子类实现一个公共父类,同时Term类只需要在放一个ArrayList<Factor>即可,不需要放置6种不同的类,这样一来操作比较方便,或者只是对嵌套因子类和表达式因子类的存放做出改变,采用ArrayLsit替代数组,可以减小编程难度。可以采用工厂模式。



