数论的一些听不懂的东西

大总结 https://www.cnblogs.com/YoungNeal/p/8908187.html

https://www.luogu.org/blog/violet2333/shu-lun

逆元

https://www.cnblogs.com/zhangjiuding/p/7546158.html

https://www.cnblogs.com/zwfymqz/p/7730375.html#_label0

 

 

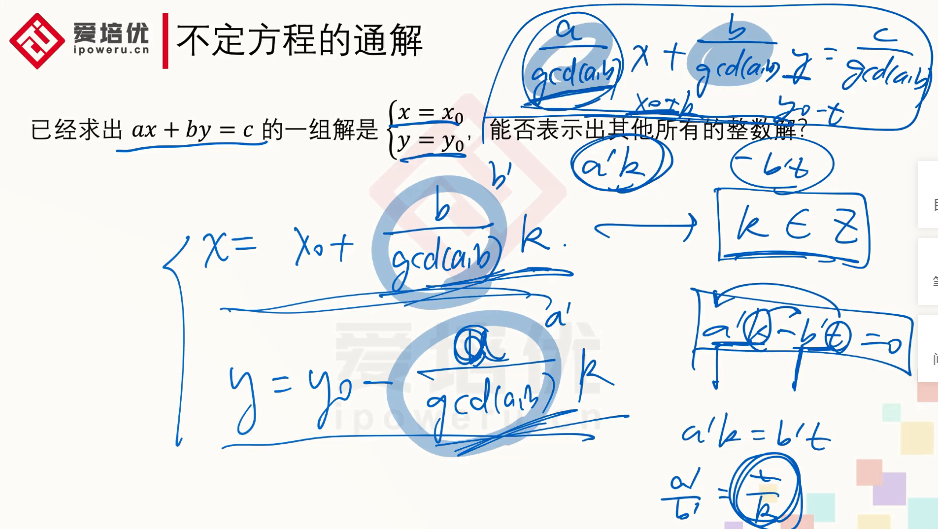
不定方程

 

 

 

 

组合数

 

 

 

 

 

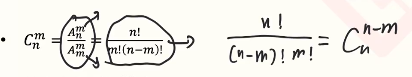
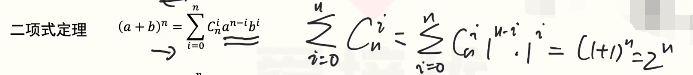
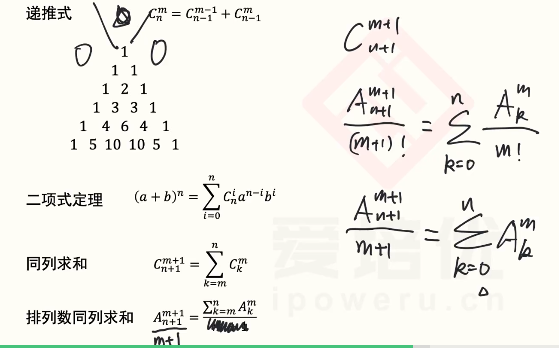
k次方

展开形式

 

  

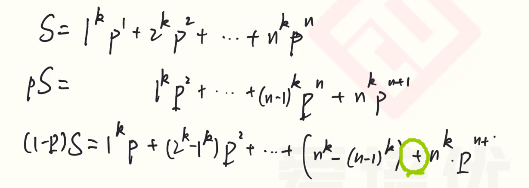
这写错了，是减

 

 

三项式定理

 

立方和推导

 

 

 

 

 

 

 

 

 

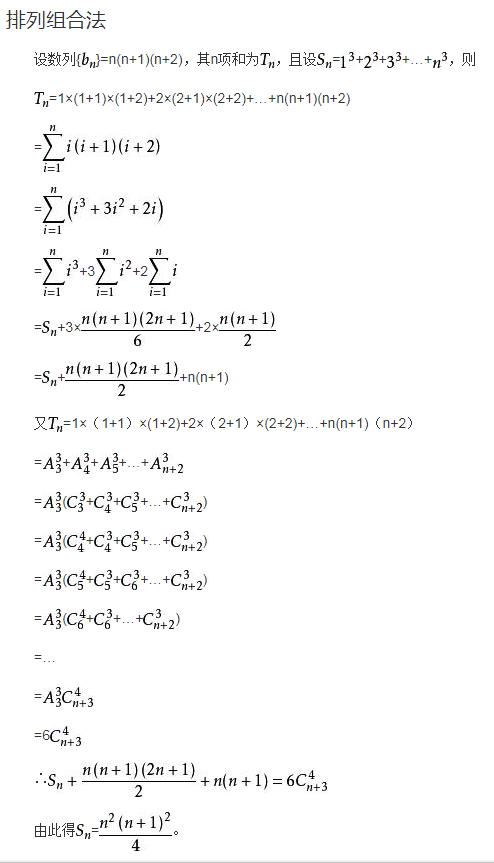
 这是个啥意思？？p是干嘛用的

 

 

卷积式

 

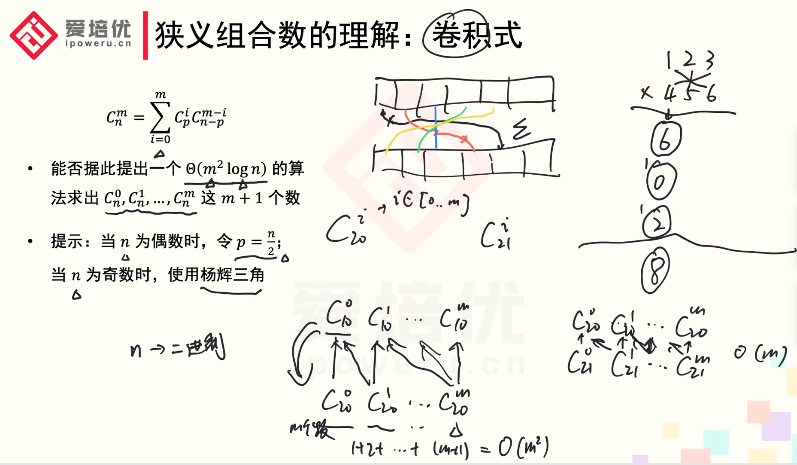
容斥原理

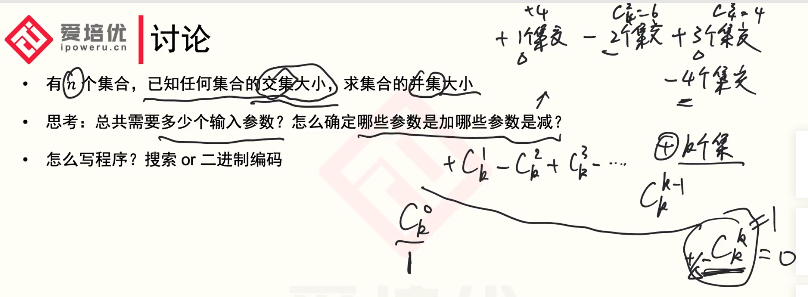
（|s|指s的元素个数）

 

 

 

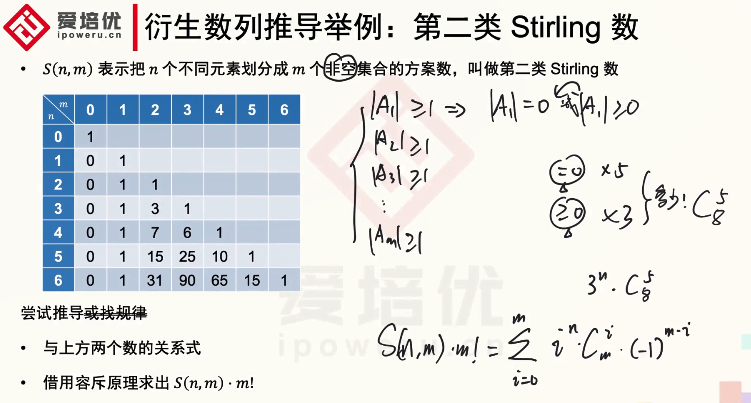
中国剩余定理

https://mp.weixin.qq.com/s?src=11&timestamp=1573172431&ver=1961&signature=rafKtTGFK4ik8VTxDpSKigQXYj2UygR5OQQthHCOss9kSzEm0xVKLO1B*touvWSf2epdaxz6yQA3UILeNvbZsKcPy236pvA1rOrvKLqiG7-N768IDjNwf0uY08E3I9Al&new=1

中国剩余定理其实只考虑两个元素的合并会好理解很多，因为n个元素先合并前n-1个以后，前n-1个模数乘起来也和第n个模数是互质的。
对于两个数的情况：x=a0(mod p0), x=a1(mod p1)
我们想办法构造一个在模p0p1意义下的式子β，使得β mod p0=a0，β mod p1=0
要让β mod p1=0，β得是p1的倍数，那么式子里面得有一个p1
那p1乘个啥玩意mod p0=a0呢？我们先想到p1乘“p1关于p0的逆元”能得到1，用1乘a0就得到了a0
因此β=p1 × p1关于p0的逆元 × a0
这样我们就构造出了mod p0=a0，mod p1=0的式子
接下来只需要再构造一个mod p1=a1，mod p0=0的式子，把它俩加起来就能达成目标

 

 

 

 

 

 

  

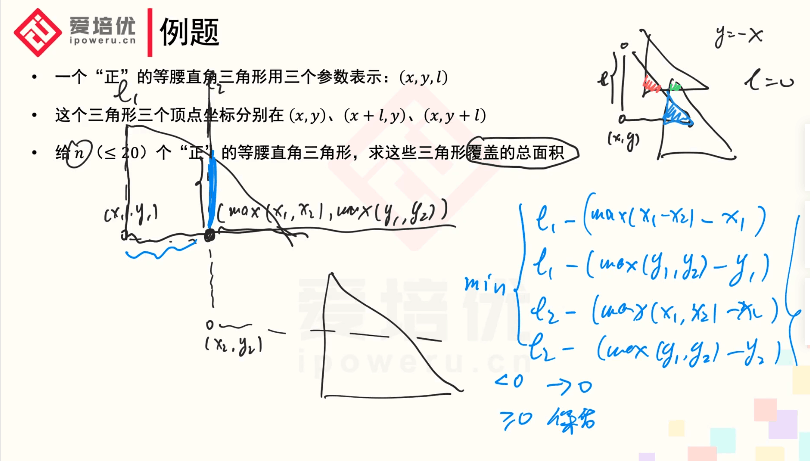
题目

1.http://oj.ipoweru.cn/problem/11408

2.http://oj.ipoweru.cn/problem/11409

3.http://oj.ipoweru.cn/problem/11411

4.http://oj.ipoweru.cn/problem/11412

5.http://oj.ipoweru.cn/problem/11415

题解：https://www.luogu.org/blog/Yang-xia-Xuetong/zu-ge-shuo-shuo-lun-xiao-jie-gui-na-pian