独立级联模型和线性阈值模型

一个社交网络通常被描述为一个有向图G=(V,E),其中V是节点的集合，E∈V×V是有向边的集合。每一个节点v∈V代表社交网络中的一个人，每一条边(u,v)∈E代表节点u到节点v的影响力关系。

边是有向的，(u,v)∈E表明节点u对节点v有影响力，反之不一定。对于(u,v)∈E，它叫做节点u的出边，节点v的入边，节点u叫做节点v的入邻居，节点v叫做节点u的出邻居。一个节点v的所有出邻居用N⁺(v)表示，所有入邻居用N^-(v)表示。

通常情况下，每个节点有两个状态：不活跃和活跃。不活跃表示该节点未收到对应实体，活跃表示该节点已收到对应实体。节点从不活跃状态转变为活跃状态称之为被激活。

独立级联模型

如图1所示，每一条边(u,v)都有一个对应的概率p(u,v)∈[0,1],表示节点v能被节点u独立激活的概率。

独立级联模型下的动态传播过程在离散时间点的形式如下：

• t=0时刻，事先选好的初始集合S₀(seed set种子节点结合)首先被激活，其他节点都为不活跃状态；
• t≥1时刻，任一在上一时刻被激活的节点u∈S_t-1\S_t-2,节点u会对他的所有尚未被激活的出邻居v∈N⁺(u)\S_t-1尝试一次激活，如果尝试激活成功，则v∈S_t\S_t-1；否则节点v仍未未激活状态，即v∈V\S_t；
• 当在某一时刻不再有新节点被激活，传播过程结束。

       注：每一个节点只有一次尝试激活其出邻居节点的机会，且发生在该节点被激活后的下一时刻。

       在影响力传播中经常关系的是传播结束后被激活节点个数的期望值，即E[|S_∞|]，用σ(S₀)表示，并称之为最终的影响力延展度。

 

 

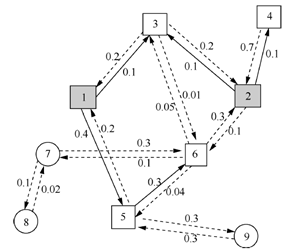
图 1 独立级联模型示意图

       独立级联模型抽象概括了社交网络中人与人之间独立交互影响的行为。它通过边上的概率来描述人与人之间发生影响的可能性和强度。很多简单实体（如新消息在在线网络的传播或新病毒在人际间的传播）很符合独立传播的特性。独立级联模型也在基于实际数据的影响力学习中被初步验证是有效的。所以独立级联模型是目前研究最广泛、最深入的模型。

 

线性阈值模型

线性阈值模型中，每条有向边(u,v)∈E上都有一个权重值w(u,v)∈[0,1]。w(u,v)反应节点u在节点v的所有入邻居中影响力重要性占比，要求∑_u∈N-(v)w(u,v)≤1。每个节点都有一个被影响的阈值θ_v∈[0,1]。

线性阈值模型下的动态传播过程在离散时间点的形式如下：

• t=0时刻，事先选好的初始集合S₀(seed set种子节点结合)首先被激活，其他节点都为不活跃状态；
• t≥1时刻，每个不活跃的节点v∈V\S_t-1都需要根据它所有已经激活的入邻居到它的线性加权和是否达到它的被影响值来判断是否被激活，即是否满足∑_{u∈N-(v)∩St-1}w(u,v)≤θ_v。如果满足则节点v被激活，否则仍保持未激活状态。
• 当在某一时刻不再有新节点被激活，传播过程结束。

线性阈值模型中节点v的阈值θ_v表达了节点对一个新的实体的接受倾向：阈值越高，节点v越不容易被影响；反之阈值越低越容易被影响。

节点v的入邻居对节点带的影响是联合发生的，可能任何一个入邻居都不能单独激活节点v，但几个入邻居联合起来就可能使对节点v的影响力权重超过节点v的阈值，从而激活几点v，这对应了人类的从众行为，也是和独立级联模型的主要不同之处。

线性阈值模型的随机性完全是由节点的被影响阈值决定，一旦阈值确定，后面的传播过程就是完全确定的。这是线性阈值模型不如独立级联模型应用广泛的一个原因。

 

参考文献：陈卫，微软亚洲研究院 .社交网络影响力传播研究 . doi: 10.11959/j.issn.2096-0271.2015031