时间复杂度与基本排序算法
时间复杂度与基本排序算法
一.时间复杂度
时间复杂度是用来描述一个算法的,从字面意义我们不难理解,时间复杂度就是用来描述一个算法所需要的时间。用来估计常数操作的一种指标
我们首先来从常数操作的概念入手。
int a=arr[i];
这就是个典型的常数操作,执行的时间和这个数组的数据量没有关系,单纯只是数组寻址,将i位置的值赋给整型变量a而已,无论数组里只有10个元素还是有10000个元素,耗时依旧。
int b=list.get(i);
但如果我们要从链表中获得一个值,这将不是个常数操作,因为无论是单链表还是双链表,如果你想获得i位置的值,你都要从左到右遍历,直到i位置,再将其值赋给a,显而易见这不是个和数据量没有关系的操作。
除了上述所提到的两个例子外,我们所熟知的加减乘除也是常数操作,位运算也是常数操作(下面会涉及).
下面我们正式开始介绍时间复杂度。
我将通过选择排序的算法来引入时间复杂度的概念:
选择排序:
1.有一个大小为N的数组,从下标0至N-1进行遍历,并将最小的数字与0位置进行交换
2.从下标1至N-1进行遍历,并将最小的数字与1位置的数字进行交换
3.以此类推,再从下标2至N-1进行遍历,并将最小的数字与2位置的数字进行交换
4.最后就可得到一个从小到大排列的数组了
那么这个算法的时间复杂度到底是多少呢?我们采用如下的方式来定义时间复杂度:
首先不难看出,我们要对数组中每个位置的数字看一眼,一共就是N眼,这是常数操作。之后我们还要进行比较大小的操作,来找到最小的那个数字,N个数就需要比较N次,这也是常数操作。最后还要进行一次交换操作。这就是第一次遍历过程中所进行的全部操作。
承接上面的逻辑,第二次遍历我们需要看N-1眼,进行N-1次比较,最后进行一次交换操作。就这样一直到最后的遍历结束。我们来列一个表格分析一下。
看的次数:N+N-1+N-2+N-3+……
比较次数:N+N-1+N-2+N-3+……
交换次数:1+1+1+1+1+……
除交换次数外,这明显就是等差数列的求和问题,我们套入首项末项的等差求和公式,可以得到看的次数与比较次数各自的次数和,最终我们将两个次数和进行相加操作,合并同类项,并在式子最后加入我们之前扔掉的交换次数的次数和,就可以得到一个数学表达式。
aN²+bn+c
不难理解,这个表达式估计了选择排序的常数操作次数。于是我们便称选择排序这个算法的时间复杂度为O(n²),其中O叫做BigO,代表上限,可以理解为一个算法的最差情况下的时间复杂度,我们一般都用这种复杂度来评估算法,还有其他两种时间复杂度,分别为θ(f(n))与Ω(f(n)),其中前者代表这个算法平均的时间复杂度,一般在工程中使用,因为工程人员认为一个算法有好情况也有坏情况,平均值更加可靠;后者代表最好情况下的时间复杂度(有些算法会因为数据的状况不一样而导致时间复杂度不同,下面会讲到)。
不难发现,选择排序的时间复杂度括号中为N²,我们将表达式中除最高项的其他项都抹去,只留下最高项,甚至连最高项的系数也抹去,剩下的表达式为f(N),即为括号里的内容。这就是时间复杂度。
所以当你想了解一个算法的时间复杂度,你一定要非常清晰的理解这个算法的思路,因为只有这样你才能进一步计算其常数操作的表达式。
讲完了时间复杂度,我们再来讲一下额外空间复杂度。
何为额外空间复杂度呢?如果在程序运行的过程中,不需要额外的数据结构,只是用额外的几个变量,那么额外的空间复杂度就是O(1)。相反的,如果我们申请了一个和原数组大小一样或一半大小的数组,额外空间复杂度就为O(n)。
二.位运算
现代计算机中的所有数据都是以二进制形式存储在设备中,为0和1两种状态,计算机对二进制数据进行的运算即为位运算,位运算有&、|、^、~、>>、<<这几种,位运算的速度比四则运算来的还要快。
这次文章里我们只用异或运算与和运算。
首先将异或运算,异或运算的符号为,ab即为a与b进行异或运算,我们规定,两个位相同为0,相异为1,举个例子:
以上即为异或运算的运算规则,除此之外,我们还需要了解几条异或运算的性质:
1.异或运算满足交换律与结合律
ab=ba (ab)c == a(bc)
2.对于任何数x,都有 xx=0,x0=x
理解过来也就是,0与任何数异或等于任何数,任何数与自身异或等于0
3.自反性: abb=a^0=a;
这个不难理解,但是十分重要,下面会主要用到这条性质。
4.如果有一群数字,无论他们异或的顺序如何,只要数字全部相同,那么顺序不会影响最终的异或结果
我们来更深一步理解异或运算,并初步运用异或运算进行一些操作。
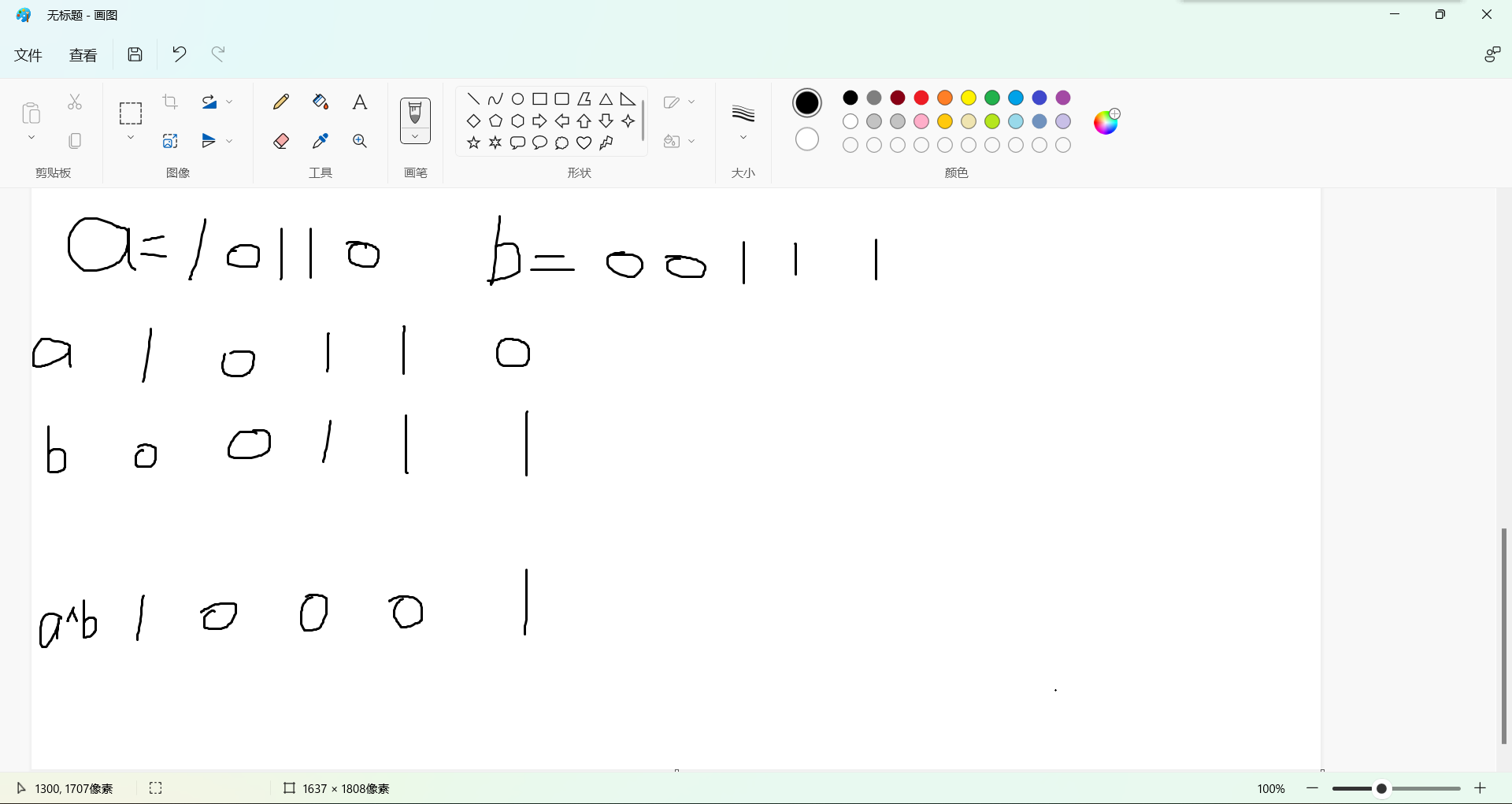
eg:假如我们现在有两个数a和b,a=10110,b=00111,那么a^b为多少呢?
位运算是位与位相对的运算,我们需要进行一位一位的异或运算。如下图所示
1.从左到右进行第一位的异或运算 0^1=1
2.第二位的异或运算 1^1=0 第三位 1^1=0 第四位 0^0=0 以此类推
3.最终我们得到a^b=10001
我们当然可以将异或运算在画图中进行这样的操作,就像列竖式一样,但我们不难发现还有一种规律隐藏在异或运算中,我们不妨来将异或运算看作是一种不进位的二进制运算,更深层次的理解异或运算。
1.从左到右 0+1=1 不足2不进位 为1
2.第二位 1+1=2 足2为0但不进位
3.第三位 1+1=2 足2为0但不进位
4.第四位 0+0=0 以此类推
5.最终我们一样得到了10001这个结果
很好,现在看来我们更深层次理解了异或运算这样一种位运算,如此的神奇与美丽,有人可能问,我们为什么要从这个角度来理解异或运算呢?我也可以根据上面的运算规则进行一位一位的运算啊,我们从不进位二进制的角度来理解会对你在性质的推导方面有极大的便利,如果你对一般性质的推导也从第一个层面来入手,我认为你多半会在挫败中失去开工之前的兴致。再者,深层次理解一种运算的规律,这本身也是十分令人欣喜的。
应用:Swap
到目前为止,你已经可以说自己认识了异或运算了,那么我们能用目前所掌握的异或知识做些什么呢?你可以用来写一个swap函数:
//此处使用Java,因为下面我要用语法糖,C语言直接把前面的类什么的内容换成void即可
public static void swap(int[] arr,int i,int j){
arr[i]=arr[i]^arr[j];
arr[j]=arr[i]^arr[j];
arr[i]=arr[i]^arr[j];
}
你现在可能看完后一头雾水,这怎么就把两个数值进行交换操作了呢?不用着急,我们来一行行看这个函数体。
首先我们来用一个简单的顺序理解上面的代码,而不是一上来就从数组入手。
a=a^b;
b=a^b;
a=a^b;
如果你想交换两个变量的数值,那么你只需要运行这三行代码即可,为什么?
1.首先第一行,我们将a^b这个值通过等号运算符赋给a
2.第二行 我们将ab赋给b,但注意,此时的a已经是ab了,所以b现在为abb,你可能已经发现问题的重要性了,快用你的鼠标中键把cursor变成箭头状,翻到上面的异或运算第三条性质,abb不就是a本身吗?此时我们就将a的值赋给了b。
3.第三行 此时的ab便是aa^b,毫无疑问了,这就是b,我们成功将b的值赋给了a
4.到此为止,我们顺利完成了a与b的数值的交换
此时你可能会很高兴,觉得这个方法真是太装逼了,再也不用像翁恺老师说的那样,我还要用第三个空杯子先把值传给它才行,太酷炫了。
但我下面要说的就是这个方法的问题,换句话说,我并不推荐你以后用这样的方法来进行数值的交换。
首先,位运算确实要比我们使用temp来进行交换来的快,而且也不需要申请一个新的变量来储存你需要交换的数据中的一个,但是这不足以让他在这场较量中获胜。
异或运算的问题就在于,如果这需要交换的两个数值在内存中不是两块独立存在的区域,那么这个方法就会出错,这一个问题就十分致命,但我们依然可以通过上面的这个swap来获得一些学习异或运算的成就感,你也可以继续往下看下去。
我们现在就不难理解上面的代码了,其实就是把arr[]这个数组中i位置和j位置的数字进行互换而已。
三.面试真题
我们来通过上面所学的知识看一道面试题,但是要解决下面这道面试题,你还需要了解一下取反与和运算,不过不用担心,我会在解题过程中写入这两种运算的讲解。
题目内容:
有一个整型数组,数组中有许多的数字。
(1)其中有一种数字出现了奇数次,而其他数字都出现了偶数次,请你找到这个数。
(2)其中有两种数字出现了奇数次,而其他数字都出现了偶数次,请你找到这两个数。
以上两问的算法都要求时间复杂度为O(N),额外空间复杂度为O(1)。
我希望你能花2分钟时间认真想一下思路,看看自己能不能通过对付这道题来说足够的知识储备来解决,虽然熟练度肯定有所欠缺,但我想大概的思路还是不难的,如果你想到了,或是毫无头绪,再来看下面的内容。
我们首先来对付第一问:
1.首先我们申请一个名为eor的整型变量,将其初始化为0.
2.将eor从数组中第一个元素异或至数组中最后一个元素,最后的eor即为那个出现了奇数次的数。
代码部分:
public static void question1(int[] arr){
int eor=0;
for(int cur:arr){
eor^=cur;
}
//for循环中的参数为语法糖,如果用C的话,和for(int i=0;i<n;i++)为一个意思,都是遍历
System.out.println(eor);
}
什么?就这么短吗?确实就这么短,但是里面蕴含的内容我们还是要详细了解一番。
1.我们不妨假设数组中的a出现了奇数次,其他数字例如b出现了偶数次
- aaaaa=a 不难理解,此处不做解释,一步步运算即可。
bbb^b=0 同样不做详解
3.由2我们不难了解到,如果一个数字本身异或奇数次,那么最后还会得到它本身,如果一个数字异或偶数次,那么最后会得到0.
4.不妨令第一个出现的数字就为a eora=0a=a
5.之后eorbbbbbb 无论有多少个b,最后所有的b都将为0,而eor与0异或,还会得到eor本身,也就是出现奇数次的那个a。
6.于是最后我们只需要将eor输出即可了
第一问只是个送分题,第二问虽然只是多了一个数,但我们就需要动点脑子了。先贴上代码部分,有了上一道题目的铺垫,我想通过阅读第二问的代码,大多数人也能灵光一闪了,甚至有些人应该不用阅读也可以做出第二问。
public static void question2(int[] arr){
int eor=0,onlyOne=0;
for(int curNum:arr){
eor^=curNum;
}
int rightOne=eor&(~eor+1);
for(int cur:arr){
if((cur&rightOne)==0){
onlyOne^=cur;
}
}
System.out.println(onlyOne+""+(eor^onlyOne));
}
1.我们还是承接上一问的思路,这次我们不妨设a与b都出现了奇数次,那么a与b之前所有出现偶数次的数字最后都是一个0,不用管他们,最后肯定会剩下eor=a^b,此时我们知道a与b是不相等的,所以a与b异或出来的结果中一定至少有一位不为0,而这(些)位置便是a与b的二进制中不同的位置。
2.此时我们申请一个eor‘这个变量,将eor’与数组中不是0的那一位上为0的数字进行异或,那么a与b中肯定会少去一个,最后得到的eor‘即为a与b中的某一个,大功告成,我们此时只要将eor’与eor异或即可得到另外一个数了。
思路就是这样,理解上面的代码应该就不难了,但是&和~又是什么意思呢,这就是开头说好要讲的剩下的位运算。
&为和运算,它的运算规则是:
~为取反运算,它的运算规则是:
到此为止,这道面试题我们就成功解决了。
四.插入排序
在最后,我们再来讲一种排序方法,叫做插入排序
我们现在有这样一个数组(如上图),要对数组进行从小到大的数字排序,我们该如何做呢?
1.首先我们来做到0-0位置上的数字有序,我们已经实现了
2.接着我们来做到0-1位置上的数字有序,因为3>1,所以我们不需要进行交换
3.之后我们来做到0-2位置上的数字有序,因为2<3,所以两个位置需要进行一个交换,之后2>1,所以不用继续交换
4.以此类推,其实就是从1的位置从后往前看,如果后一个数小于前面的数字,那么两个数字就要交换位置,反之或是前面没有了数字,那么便不再需要进行交换,按照这个方法循环至最后一位即可了。
那么为什么要讲这样一种排序方法呢?因为它和冒泡排序以及选择排序的时间复杂度不同,它的时间复杂度受数据状况的影响。
如果数组为7654321,那么我们需要进行0+1+2+3+4+5+6次交换,和选择排序相同,时间复杂度为O(N²),但若此时的数组情况为1234567,那么我们一次交换也不需要,只需要看一眼所有的数就行,都是常熟操作,时间复杂度就是O(N)。
但时间复杂度,我们一般均用最坏的情况来估计,而非使用最好或是平均。

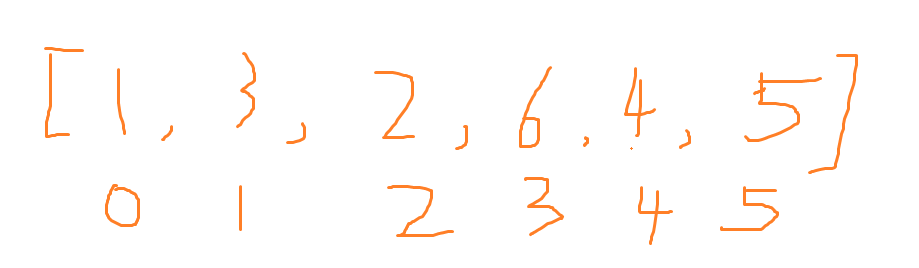

 浙公网安备 33010602011771号
浙公网安备 33010602011771号