Leetcode刷题笔记(双指针)
1.何为双指针
双指针主要用来遍历数组,两个指针指向不同的元素,从而协同完成任务。我们也可以类比这个概念,推广到多个数组的多个指针。
若两个指针指向同一数组,遍历方向相同且不会相交,可以称之为滑动窗口(两个指针包围的区域为当前的窗口),经常用于区间搜索。
若两个指针指向同一数组,但是遍历方向相反,那我们可以用来进行搜索,这时我们要搜索的数组往往需要排序好。
2.双指针类型
在目前的刷到过的题目种,遇到了两类双指针问题
第一类是快慢指针,顾名思义,就是一个fast指针,一个slow指针,一前一后,一般用来解决链表中的问题。方向相同。只是一般,也有一些数组问题可以用快慢指针解决,所以如果按使用对象来分,是十分不严谨的。
第二类是左右指针,实际上指的是两个索引值,一般用来解决数组中的问题。也有人叫这个方法对撞指针。方向相反。
3.左右指针
我打算先从左右指针来讲起,符合我大一先学习了数组再学习链表这一顺序,至少数据结构中顺序也是如此吧.
i>二分查找
我们可以将二分查找看作为双指针的一种特殊情况,一般情况下会将二者区分开来,双指针类型的题目,指针通常是一步一步移动的,而在二分查找里,指针每次移动半个区间长度
二分查找不过多在此文内赘述,只是当作一个非常简单的引入,关于详细的二分查找会另起一篇。在这里书写一个最简单的二分查找法
class Solution{
public:
int BinarySearch(vector<int>& nums,int target){
int left=0,right=nums.size()-1,mid;//因为是数组,所以我们要size-1
//我们添加等于号的原因是,如果当区间内只有一个数字时,无等号将会陷入死循环
while(left<=right){
mid=left+(right-left)/2;//这里等价于(left+right)/2,但我们不这么写的原因是,为了防止数据太大炸掉
if(nums[mid]==target){
return mid;
}else if(nums[mid]>target){
right=mid-1;
}else{
left=mid+1;
}
}
return -1;//如果查找不到,我们返回-1
}
};
二分查找是一种理解起来十分简单,时间复杂度非常优秀的算法,我们只需要O(logn)的时间复杂度就可以完成查找
相关题目:
Leetcode 704 二分查找 代码同上述 不在此贴出解法
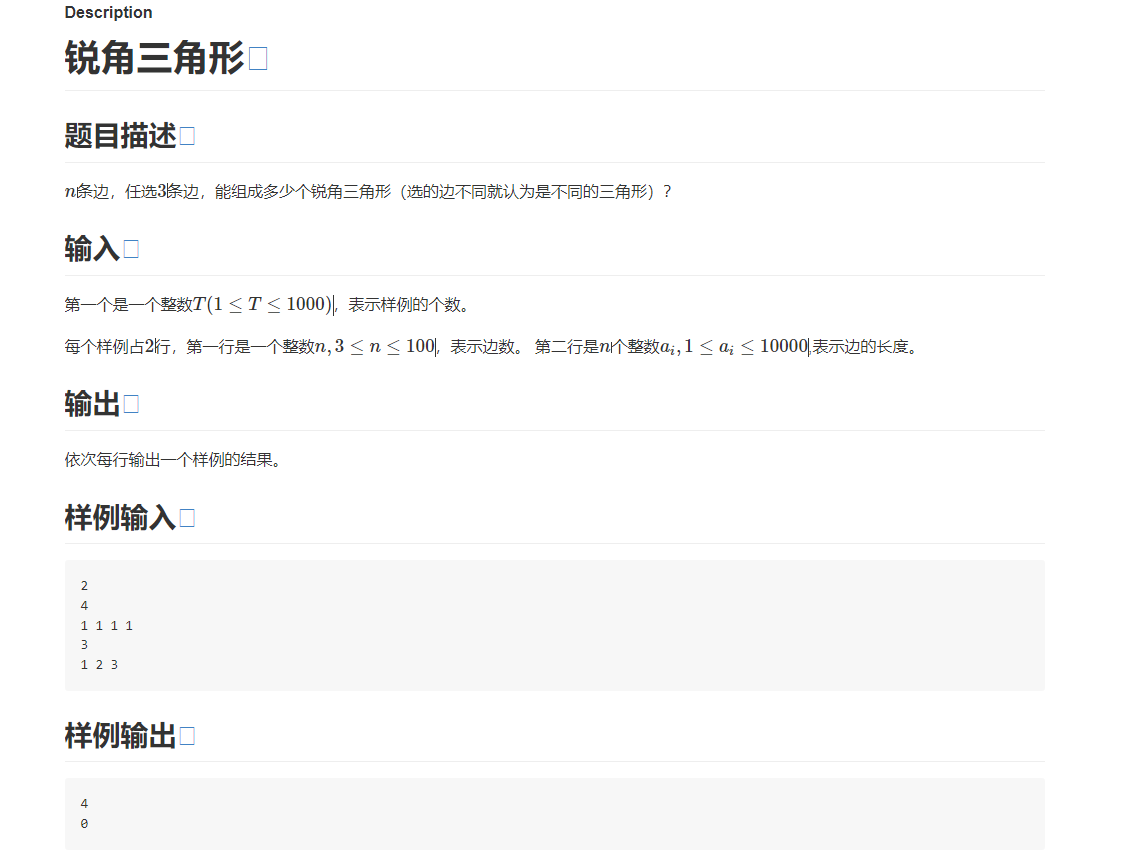
2021大一C语言程序设计模拟考试 锐角三角形
#include "stdio.h"//为了使用C风格的输入输出,加快速度
#include "algorithm"
using namespace std;
int side[105];
int main(){
int t;
scanf("%d",&t);
while(t--){
int n,ans=0;
scanf("%d",&n);
for(int i=0;i<n;++i){
scanf("%d",&side[i]);
}
sort(side,side+n);
for(int i=0;i<n;++i){
for(int j=i+1;j<n;++j){
int left=j+1,right=n-1,k=j;
while(left<=right){
int mid=left+(right-left)/2;
if(side[mid]*side[mid]<side[i]*side[i]+side[j]*side[j]){
k=mid;
left=mid+1;
}
else{
right=mid-1;
}
}
ans+=k-j;
}
}
printf("%d\n",ans);
}
return 0;
}
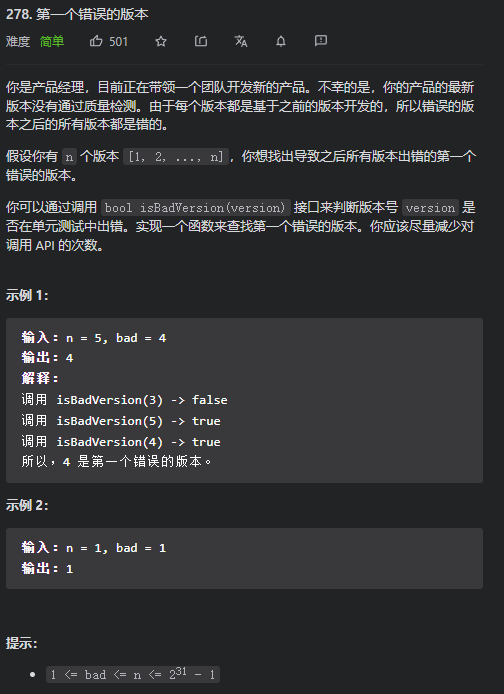
Leetcode 278 第一个错误的版本
思路:
我们不难理解,调用isBadVersion这个API所返回的类型为bool,也就是说,非零即一,且1之后的所有数字都会为1,就像是{0,0,0,0,0,1,1,1,1,1}这样,完美符合二分查找所需要的条件,数组有序。
题目就是要我们寻找第一个为1的元素,返回其下标即可,综上,我们不难想到只需要利用二分查找,将区间逼至只有一个数即是。
代码:
//iSBadVersion已经定义完毕 无需我们敲入
class Solution {
public:
int firstBadVersion(int n) {
int left=1,right=n,mid;
while(left<right){
mid=left+(right-left)/2;
if(isBadVersion(mid)){
right=mid;
}else{
left=mid+1;
}
}
return left;
}
};
//时间复杂度为O(logn) n为版本数量 空间复杂度为O(1) 我们需要常数空间保存若干变量
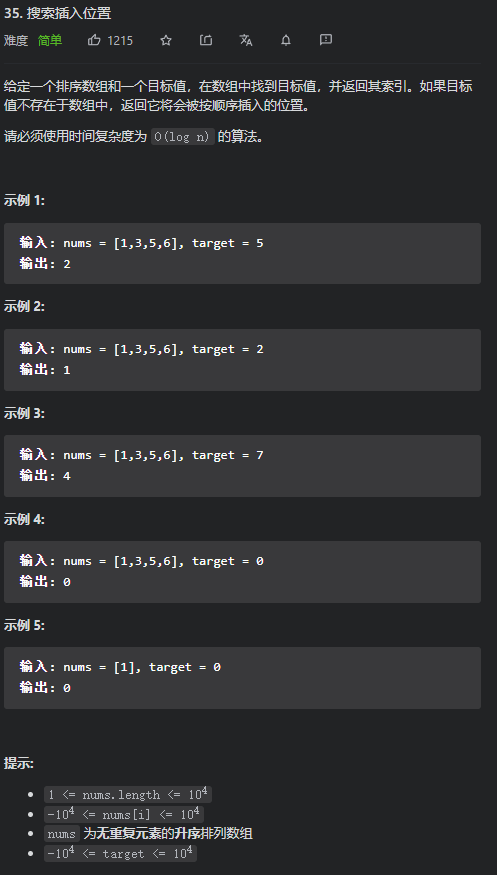
Leetcode 35 搜索插入位置
思路:
仁慈的简单题我重拳出击 我们发现,一查找元素 二数组有序 就已经想到要用二分查找了,并且本题还特意仁慈的告诉我们必须要实现O(logn)的算法,那必然就是二分查找了。
有人可能会疑问,我们还要考虑目标值如果不在数组中,返回它要按序插入的位置,这样还能用二分查找吗,当然是可以。
重新考虑题意,假如我们现在要在pos这个位置插入,它应该满足这样一个条件
如果数组中现在存在这个值,要返回的索引也是pos,因此我们将两个条件合并,无论哪种情况,我们只需要输出在一个有序数组中第一个大于等于target的下标。
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left=0,right=nums.size()-1,ans=nums.size();//我们这里设置一个ans为数组长度,可以省略边界条件的判断 当target大于数组中所有数时 我们需要插入到数组长度的位置
while(left<=right){
//mid这句也可以写成int mid=((right-left)>>1)+left
int mid=left+(right-left)/2;
//当右指针移动超过左指针后,我们停止查找,终于找到了那一个数字
if(nums[mid]>=target){
ans=mid;
right=mid-1;
}else{
left=mid+1;
}
}
return ans;
}
};
得益于C++强大的STL,我们还可以使用一句话解法(用一句话木马那味了)
return lower_bound(nums.begin(),nums.end(),target) - nums.begin();
//我们来解释一下lower_bound,其功能为在一个排序好的数组内进行二分查找,与之相对应的是upper_bound()
//lower_bound( begin,end,num):从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字,找到返回该数字的地址,不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。
//upper_bound( begin,end,num):从数组的begin位置到end-1位置二分查找第一个大于num的数字,找到返回该数字的地址,不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。
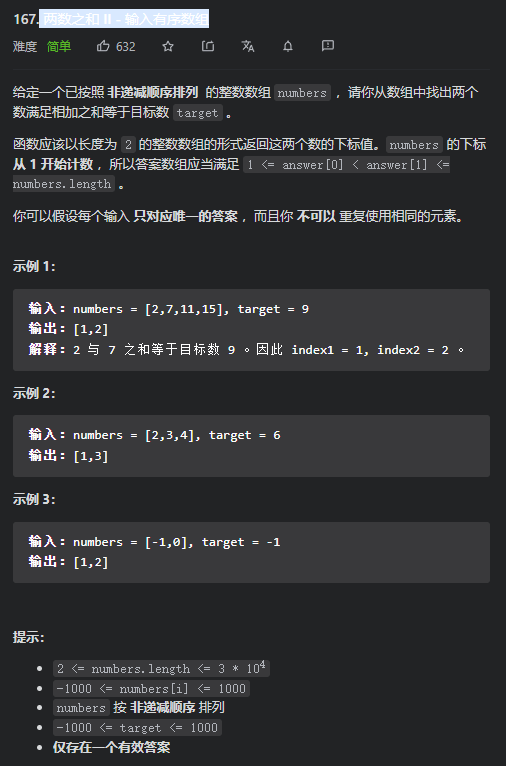
Leetcode 167 [ 两数之和 II - 输入有序数组]
思路:经典Leetcode第一题两数之和的升级版本,我们还可以利用暴力的方法或者哈希表的方法进行解题,但是就没什么意思了,我们这次用二分查找来解决这个问题。
先固定一个数字,然后第二个数字依次从左到右进行遍历,寻找其是否为target-nums[i],如果是,那么我们就找到了,返回{i+1,mid+1}即可。为了提高效率,我们使用二分查找(数组已有序),且每次均从当前固定的数字的右侧开始寻找。
代码:
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
for(int i=0;i<numbers.size();++i){
int left=i+1,right=numbers.size()-1;//left定义为i+1,每次从当前固定数字右侧开始
while(left<=right){
int mid=left+((right-left)>>1);
if(numbers[mid]==target-numbers[i]){
return {i+1,mid+1};
}else if(numbers[mid]>target-numbers[i]){
right=mid-1;
}else{
left=mid+1;
}
}
}
return {-1,-1};
}
};
II>除了二分查找之外的双指针例题
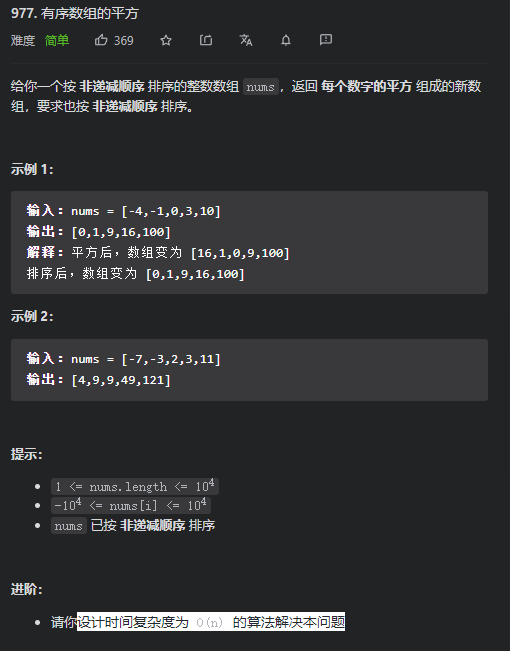
Leetcode 977 有序数组的平方
思路:
首先最简单的方法就是将数组中的元素平方压入动态数组后进行排序即可。但这样问题在于时间复杂度为O(nlogn)
双指针的思路有两种,我们一个一个说。
第一种双指针的思路是,由于暴力方法没有充分利用数组nums已经按照升序排列这个条件,所以我们可以利用这点进行改进,不难发现,当负数平方后,呈单调递减排列,非负数平方后,呈单调递增排列,我们可以在数组中找到非负数与负数的交界点boundary,然后将数组平方,两个指针依次指向boundary和boundary+1,比较两个指针所代表元素的大小,将小的放入答案并且移动相应的指针,当一边的指针移动至边界时,另一边的元素顺序放入答案中即可。
但上述这种双指针的思路还不是最优的,我们还有一种倒序双指针的思路。
第二种双指针的思路,我们可以用两个指针分别指向0和n-1,每次比较两个指针对应的数,选择较大的那个逆序放入答案并移动指针。如果我们采用这种方法,那么就无需处理某一指针移动到边界的情况了。
代码;
//第一种 暴力法
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
vector<int> ans;
for(int num:nums){
ans.push_back(num*num);
}
sort(ans.begin(),ans.end());
return ans;
}
};
//第一种双指针
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int n = nums.size();
int negative = -1;
for (int i = 0; i < n; ++i) {
if (nums[i] < 0) {
negative = i;
} else {
break;
}
}
vector<int> ans;
int i = negative, j = negative + 1;
while (i >= 0 || j < n) {
if (i < 0) {
ans.push_back(nums[j] * nums[j]);
++j;
}
else if (j == n) {
ans.push_back(nums[i] * nums[i]);
--i;
}
else if (nums[i] * nums[i] < nums[j] * nums[j]) {
ans.push_back(nums[i] * nums[i]);
--i;
}
else {
ans.push_back(nums[j] * nums[j]);
++j;
}
}
return ans;
}
};
//第二种双指针
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int n = nums.size();
vector<int> ans(n);
//pos从n-1开始
for (int i = 0, j = n - 1, pos = n - 1; i <= j;) {
if (nums[i] * nums[i] > nums[j] * nums[j]) {
ans[pos] = nums[i] * nums[i];
++i;
}
else {
ans[pos] = nums[j] * nums[j];
--j;
}
--pos;
}
return ans;
}
};
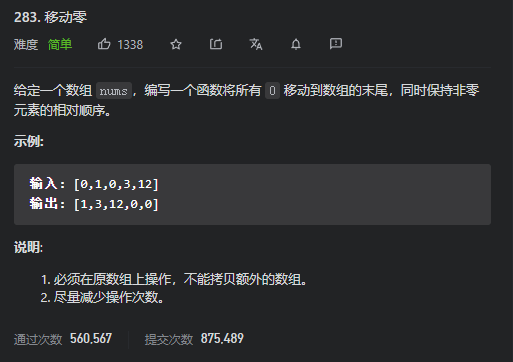
Leetcode 283 移动零
思路:
我们可以参考快排的思想,用一个待分割的元素坐中间点x,然后把所有小于等于x的元素放到x的左边,大于x的元素放到其右边
我们可以用0当做这个中间点,把不等于0的元素放到左边,等于0的放到右边。使用两个指针i和j,只要nums[i]!=0,我们就交换nums[i]和nums[j]
代码:
class Solution {
public void moveZeroes(int[] nums) {
if(nums==null) {
return;
}
//两个指针i和j
int j = 0;
for(int i=0;i<nums.length;i++) {
//当前元素!=0,就把其交换到左边,等于0的交换到右边
if(nums[i]!=0) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j++] = tmp;
}
}
}
}
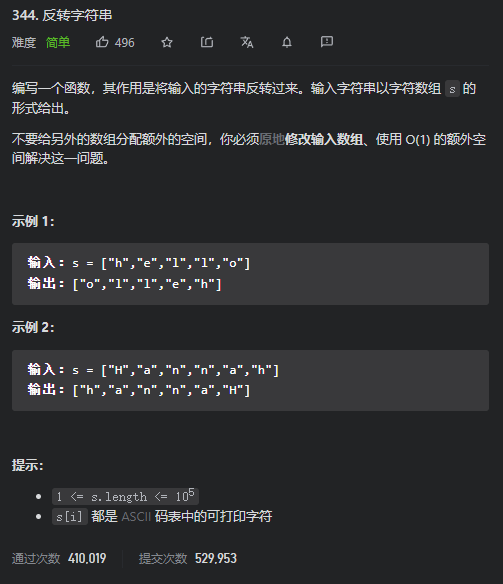
Leetcode 344 反转字符串
思路:
说实在的,这个题和上买那几个题根本没法比。
一个指针指向头,一个指针指向尾,互相交换,最终两指针相遇结束即可
代码:
class Solution{
public:
void reverseString(vector<char>& s){
int left=0,right=s.size()-1;
//这里我们不加等号
while(left<right){
swap(s[left],s[right]);
++left;
--right;
}
}
};
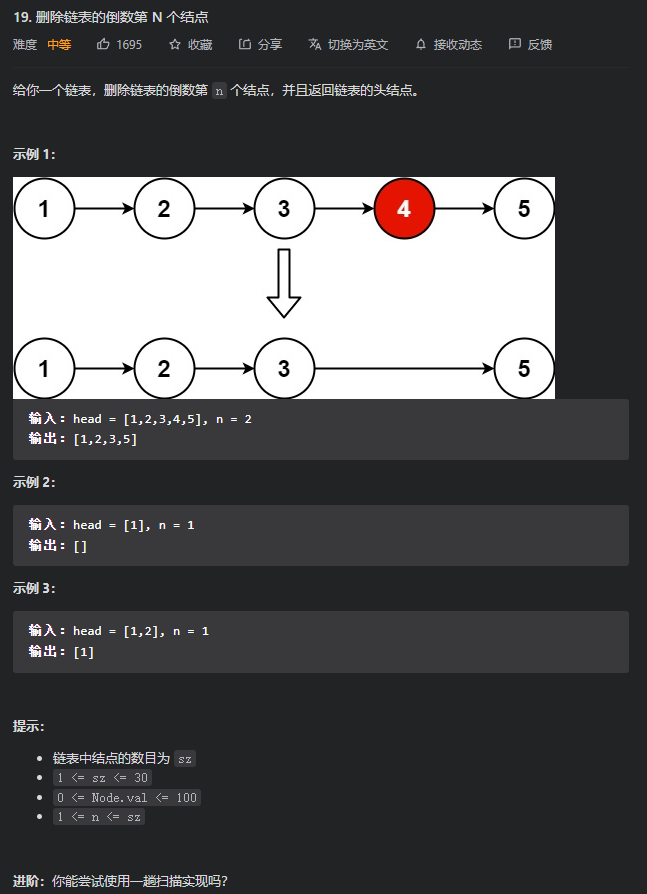
Leetcode 19 删除链表的倒数第 N 个结点
思路:
如果这是个数组,我们要删除倒数第N个元素,可以使用双指针,快慢指针指向同一个元素,首先让fast先移动n步,然后再让fast和slow同时移动,直到fast指向了数组的末尾,我们删掉slow所指向的下一个元素就行了。
如果是链表的话,我们删除一个结点的理想操作最好不是指针指向这个结点去删除,这要会导致前后断节,理想的操作是指向要删除的结点的前一个结点,把指针指向下一个节点的下一个节点,然后把要删除的结点delete或者free掉就行。所以我们在数组的基础上改一改,首先我们还是让fast和slow指向同一个节点,然后先让fast走n+1步,为什么这里要n+1步呢,因为在数组中我们以移动到末尾元素来作为快指针停止的标准,而这里我们选择快指针移动到nullptr来作为结束,多走了一步,那我们前面就要补上一步(可能我说的不太好)。但实际上我们还是可以让快指针先移动n步,只不过就是while的判断条件变为指向的结点的指针域指向为nullptr,但这样对于链表来说,删除就不方便了。之后的操作便是一样的,让快慢指针一起移动,删除慢指针指向的下一个结点就行了。
代码:
class Solution{
public:
struct ListNode{
int val;
ListNode* next;
ListNode(int val):val(val),next(nullptr){}
};
ListNode * removeNthFromEnd(ListNode* head,int n){
ListNode * dummyHead=new ListNode(0);
dummyHead->next->head;
ListNode* fast=dummyHead;
ListNode* slow=dummyHead;
while(n--&&fast!=NULL){
fast=fast->next;
}
fast=fast->next;
while(fast!=NULL){
fast=fast->next;
slow=slow->next;
}
ListNode* temp=slow->next;
slow->next=slow->next->next;
delete temp;//防止内存泄漏
return dummyHead->next;
}
};
Leetcode 141 环形链表
思路:
对于链表找环路的问题,有一个通用的解法——快慢指针(Floyd判圈法)。给定两个指针,分别命名slow和fast,起始位置在链表的开头。每次fast前进两步,slow前进一步。如果fast可以走到尽头,那么说明链表没有环路;如果fast可以无限走下去,那么说明一定有环路,且一定存在一个时刻slow和fast会相遇(fast先进入了圈子开始兜圈,后面slow进入,就相当于是一个追及相遇问题了)。当slow和fast第一次相遇时,我们将fast重新移动到链表开头,并且让slow和fast每次都进一步,当slow和fast第二次相遇时,相遇的节点即为环路的开始点。
Leetcode上还把这个算法叫做龟兔赛跑法,形象生动,具体解释是一样的,但是一些说法可以帮助理解,比如
代码:
//本题只是简单的判断是否为环形链表 暂时不用返回环路的开始点
class Solution{
public:
bool hashCycle(ListNode* head){
if(head==nullptr||head->next=nullptr){
return false;
}
ListNode* slow=head;
ListNode* fast=head->next;
//我们不能只判断一个fast是不是指向了nullptr这个条件,比如说fast->next如果也是nullptr,那么他肯定会到nullptr的,我们也需要把这种情况考虑进来
while(slow!=fast){
if(fast==nullptr||fast->next==nullptr){
return false;
}
slow=slow->next;
fast=fast->next->next;
}
return true;
}
};
Leetcode 142 环形链表 II
思路:
这题我们就可以使用完整版的弗洛伊德判圈法了。
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode * slow=head;
ListNode * fast=head;
//这里我们用do while,前面的快慢就可以指向同一结点了
do{
if(!fast||!fast->next) return nullptr;
fast=fast->next->next;
slow=slow->next;}while(fast!=slow);
//已判断出有环 下面我们寻找环结点入口
fast=head;
while(fast!=slow){
fast=fast->next;
slow=slow->next;
}
return fast;
}
};
2021/12/12 先写到这里 之后会继续更新题目和总结




 浙公网安备 33010602011771号
浙公网安备 33010602011771号