Crypto 杂题选做

？apj 你在干神魔

暑假好像有好多场 ctf，所以这博暑期可能还会更新几次（

目录

• W4terCTF 2024
  • Merciful ZMJ4396
  • d3
• Google CTF 2023
  • LEAST COMMON GENOMINATOR
• DeadSec CTF 2024
  • Raul Rosas
• corCTF 2024
  • steps
  • monkfish / anglerfish
• CrewCTF 2024
  • read between the lines
• CTFZone 2024 Quals
  • Shes the Real one
  • Cold Siemens
• LITCTF 2024
  • Symmetric RSA
  • Truly Symmetric RSA

W4terCTF 2024

之前朋友给我看的题

Merciful ZMJ4396

找不到原来的 task.py 了，记得大概是这么个题，口胡一下吧

有两个多项式 \(F(m) = m^{43} + 96, G(m) = (m-7)^{77} + (m+777)^7\)，要你找到一个 \(m\)，使得 \(\gcd(F(m), G(m)) > 2^{7777}\)

当时没做出来，后来看 wp 才大概看明白的

首先关于多项式 \(\gcd\) 有一些高深理论，我没太研究明白，反正大概就是有个东西叫结式（resultant），然后两个多项式的值的 \(\gcd\) 一定是这两个多项式的结式的因子，且结式的每个因子都一定可以被取到。好像通过一些对多项式做 exgcd 也能得到这个数？确实没有太研究明白就摆了，丢个 wikipedia 在这里吧。还有个关于 \(\gcd\) 值的 ref。

总而言之，对于这题来说，可以直接求一下 \(F(m)\) 和 \(G(m)\) 的结式，就能知道这两个多项式 \(\gcd\) 的最大值是多少了。设它为 \(P\)，级别大概是 \(2^{9000}\) 多的。那么现在我们只需要找到能够取到它的 \(m\) 即可。当然这好像还是不太容易，因为这等价于解 \(F(m) \equiv 0 \pmod P\) 和 \(G(m) \equiv 0 \pmod P\) 的解集的交，但是光求一个高次方程的解已经不可接受了（\(P\) 太大了无法分解，所以很难做高次剩余），所以我们还需要考虑一些东西。

实际上我们可以找一下在模 \(P\) 意义下的 \(\gcd(F, G)\)，这里是多项式的 \(\gcd\)。那么我们要的解就是 \(\gcd(F, G) \equiv 0 \pmod P\) 了。（我怎么没想到这个）但是发现模合数 \(\gcd\) 好像不一定存在，库直接没有这个的实现，那自己写一个朴素 \(\gcd\) 吧。发现确实找不到 \(\gcd\)，因为没有逆元。尝试将 \(P\) 的比较小的因子除掉（\(2^{10} | P\)），然后发现就找到 \(\gcd\) 了，而且次数很小，是个一次多项式。这样直接就解出 \(m\) 了。

from sage.all import *
from gmpy2 import *

def gcd1(a, b):
    if b == 0:
        return a.monic()
    else:
        return gcd1(b, a % b)

PR = PolynomialRing(ZZ,'x')
x = PR.gen()
f = x ** 43 + 96
g = (x - 7) ** 77 + (x + 777) ** 7
P = abs(f.resultant(g))
print(P)
P //= 2 ** 10

PR = PolynomialRing(Zmod(P),'x')
x = PR.gen()
f = x ** 43 + 96
g = (x - 7) ** 77 + (x + 777) ** 7
h = gcd1(f, g)
print(h)
# h's degree = 1
m = gmpy2.mpz(P - h[0])
ans = gmpy2.gcd(m ** 43 + 96, (m - 7) ** 77 + (m + 777) ** 7)

print(ans.bit_length())

print(m)

d3

好像是叫这个？？？我忘了，同样是找不到 task.py，数据范围也不咋记得了，直接口胡了，我只记得当时我做法是对的但是有些细节弱智了导致掉了大量精度，结果最后跑不出来答案

给你一个数 \(d\) 的立方根的小数部分，还原 \(d\)。

小数部分大概是给到了 \(2^{-1024}\) 的精度？记不太清了。

设整数部分为 \(x\)，小数部分为 \(y\)，那么 \(\sqrt[3]{d} = x + y\)，我们知道 \(y\)，现在相当于要找 \(x\)。

我们知道的信息应当是 \((x + y)^3 \equiv 0 \pmod 1\)，拆一下有 \(x^3 + 3x^2y + 3xy^2 + y^3 \equiv 0 \pmod 1\)。注意到 \(x\) 是整数，所以实际上限制是 \(3x^2y + 3xy^2 + y^3 \equiv 0 \pmod 1\)。\(y^3\) 是一个已知数，我们现在相当于要解一个关于 \(x\) 的二次方程。但是当然要注意到我们这里的精度是有限的，所以我们实际上要做的是找到一个近似解。

首先把浮点数干掉，我们左右同时乘上一个大数 \(A\)，大概 \(2^{2048}\)，取整一下，然后就可以得到一个整数的问题了。（有个傻逼先把 \(y\) 取整之后再求三次方，然后精度炸的不剩了，不说是谁）现在问题就是求 \(Px^2 + Qx + R \equiv 0 \pmod A\) 了。注意我们可以大概预估 \(x\) 的大小应该在 \(2^{300}\) 级别。这个二次很火大啊，我们考虑直接把 \(x^2\) 和 \(x\) 独立开，令 \(z = x^2\)，然后假设 \(z\) 是一个 \(2^{600}\) 级别的变量，直接跑跑看。然后这就是一个标准形式的线性同余了，可以直接上格基 LLL 了。不会的可以看看 WC 2024 游记（

我手头没代码，懒得写了！

Google CTF 2023

LEAST COMMON GENOMINATOR

ok 这题是当时闲的没事做的。来试试自己能不能做出来 google ctf 的 crypto 签到题（

但是好像也错过了 google ctf 2024，哈哈

task.py

题目大概是给了一个 LCG，你不知道它的系数，然后给出了前 6 个生成的数，然后用这个 LCG 生成了 RSA 的 key，我们的目标就是通过这 6 个生成的数还原出来这个 LCG 的系数。

LCG：\(x_i = (x_{i-1} \cdot m + c) \bmod n\)

给出了 \(x_1 \sim x_6\)，我们可以先差分一下，\(x_{i+1} - x_{i} = m(x_{i} - x_{i-1})\)，令 \(y_i = x_{i+1} - x_i\)，那么 \(y_i\) 实际上是形成了一个等比数列，\(y_i = y_{i-1} \cdot m\)。但是我们现在即不知道比也不知道模数。

考虑相邻两组，假设为 \(y_3 = y_2 m + t_2 n, y_2 = y_1 m + t_1 n\)，可以将 \(m\) 消去，得到 \(y_3 y_1 - t_2 y_1 n = y_1 y_2 m = y_2^2 - t_1 y_2 n\)，那么就有 \((t_1 y_2 - t_2 y_1) n = y_2^2 - y_3 y_1\)，这实际上告诉了我们 \(n\) 一定是 \(y_2^2 - y_3 y_1\) 的因子，而我们有 4 组这样的方程，将所有的 \(y_2^2 - y_3 y_1\) 求一下 \(\gcd\) 就能还原出来 \(n\) 了，然后就容易解出整个 LCG 了。

代码还是没有，太久之前做的题了现在没有代码了！

DeadSec CTF 2024

ok 这个是最近打的了。

有点菜！crypto 被卡了两题，虽然最后看题解发现是傻逼题，两题我想法都是对的但是一个我算的理论不可行一个我跑到一半放弃了。那两个题不写了，感觉真没意思。

Raul Rosas

task.py：

from Crypto.Util.number import * 
from sympy import nextprime

p1 = bin(getPrime(1024))[2:]
p2 = p1[:605]
p2 = p2 + ('0'*(len(p1)-len(p2)))

p1 = int(p1,2)
p2 = nextprime(int(p2,2))

q1 = getPrime(300)
q2 = getPrime(300)

n1 = p1*p1*q1 
n2 = p2*p2*q2 

e = 65537 
flag = bytes_to_long(b'REDACTED')
c1 = pow(flag,e,n1)
c2 = pow(flag,e,n2)

print(f'{n1=}')
print(f'{n2=}')
print(f'{c1=}')
print(f'{c2=}')

这个题对于 OIer 还是不太难的吧！虽然我做法可能有点偏，正解可能不是这个（

代码里 \(p_1\) 是一个随机数，\(p_2\) 是一个和 \(p_1\) 很接近的质数，\(q_1, q_2\) 是两个随机质数。然后给出了同一个 flag 的两次 RSA 加密，模数 \(n_1 = p_1^2 q_1, n_2 = p_2^2 q_2\)。由于我们知道 \(p_1\) 和 \(p_2\) 相差很小，那么 \(\frac{n_1}{n_2}\) 约等于 \(\frac{q_1}{q_2}\)，而且我们知道 \(q_1, q_2\) 的位数，我们直接找到一个 \(\frac{n_1}{n_2}\) 的最近有理逼近即可。我写的是 Stern-Broot 树上朴素二分，比较简单。

from Crypto.Util.number import * 
from sympy import nextprime
from decimal import *
getcontext().prec = 1024

n1 = 33914684861748025775039281034732118800210172226202865626649257734640860626122496857824722482435571212266837521062975265470108636677204118801674455876175256919094583111702086440374440069720564836535455468886946320281180036997133848753476194808776154286740338853149382219104098930424628379244203425638143586895732678175237573473771798480275214400819978317207532566320561087373402673942574292313462136068626729114505686759701305592972367260477978324301469299251420212283758756993372112866755859599750559165005003201133841030574381795101573167606659158769490361449603797836102692182242091338045317594471059984757228202609971840405638858696334676026230362235521239830379389872765912383844262135900613776738814453
n2 = 45676791074605066998943099103364315794006332282441283064976666268034083630735700946472676852534025506807314001461603559827433723291528233236210007601454376876234611894686433890588598497194981540553814858726066215204034517808726230108550384400665772370055344973309767254730566845236167460471232855535131280959838577294392570538301153645042892860893604629926657287846345355440026453883519493151299226289819375073507978835796436834205595029397133882344120359631326071197504087811348353107585352525436957117561997040934067881585416375733220284897170841715716721313708208669285280362958902914780961119036511592607473063247721427765849962400322051875888323638189434117452309193654141881914639294164650898861297303
c1 = 5901547799381070840359392038174495588170513247847714273595411167296183629412915012222227027356430642556122066895371444948863326101566394976530551223412292667644441453331065752759544619792554573114517925105448879969399346787436142706971884168511458472259984991259195488997495087540800463362289424481986635322685691583804462882482621269852340750338483349943910768394808039522826196641550659069967791745064008046300108627004744686494254057929843770761235779923141642086541365488201157760211440185514437408144860842733403640608261720306139244013974182714767738134497204545868435961883422098094282377180143072849852529146164709312766146939608395412424617384059645917698095750364523710239164016515753752257367489
c2 = 3390569979784056878736266202871557824004856366694719533085092616630555208111973443587439052592998102055488632207160968490605754861061546019836966349190018267098889823086718042220586285728994179393183870155266933282043334755304139243271973119125463775794806745935480171168951943663617953860813929121178431737477240925668994665543833309966378218572247768170043609879504955562993281112055931542971553613629203301798161781786253559679002805820092716314906043601765180455118897800232982799905604384587625502913096329061269176369601390578862509347479694697409545495592160695530037113884443071693090949908858172105089597051790694863761129626857737468493438459158669342430468741236573321658187309329276080990875017

e = 65537

# find approximation of n1/n2

l = (0, 1)
r = (1, 0)

def check(q1, q2):
    if q1 != 1 and n1 % q1 == 0 and n2 % q2 == 0:
        print(q1, q2)
        p2 = int(Decimal(n2 // q2).sqrt())
        d = inverse(e, (p2 - 1) * p2 * (q2 - 1))
        m = pow(c2, d, n2)
        print(long_to_bytes(m))

while l[1] < 2 ** 300 and r[1] < 2 ** 300:
    mid = (l[0] + r[0], l[1] + r[1])
    check(mid[0], mid[1])
    if mid[0] * n2 < n1 * mid[1]:
        l = mid
    else:
        r = mid

corCTF 2024

这个是在上一场 ctf 被那两题卡自闭之后弃赛来打的这场。

彩笔队友这场 pwn 和 web 一题没过，要不然还能再多点分）

steps

task.py：

from Crypto.Util.number import getPrime
from random import randint
from hashlib import sha512
from secret import FLAG

p = getPrime(1024)

def apply(x, y):
    z0 = x[0] * y[1] + x[1] * y[0] - x[0] * y[0]
    z1 = x[0] * y[0] + x[1] * y[1]
    return z0 % p, z1 % p

def calculate(n):
    out = 0, 1
    base = 1, 1

    while n > 0:
        if n & 1 == 1: out = apply(out, base)
        n >>= 1
        base = apply(base, base)

    return out

def step(x, n):
    '''Performs n steps to x.'''
    return apply(x, calculate(n))

def xor(a, b):
    return bytes(i ^ j for i, j in zip(a, b))

g = tuple(randint(0, p - 1) for _ in range(2))
a = randint(0, p)
b = randint(0, p)

A = step(g, a)
B = step(g, b)

print(p)
print(g)
print(A)
print(B)

shared = step(A, b)
assert shared == step(B, a)

pad = sha512(str(shared).encode()).digest()
print(xor(FLAG, pad))

注意到 他实际上写了个斐波那契数列，，，反正把转移矩阵写出来发现就是个斐波那契

那么实际上是给出了 \(g A^n\) 和 \(g A^m\)，可以直接解方程解出来 \(f_n, f_{n-1}\) 和 \(f_m, f_{m-1}\)，然后求 \(f_{n+m}\) 即可，可以用一下 \(f_{n+m} = f_n f_{m+1} + f_{n-1} f_{m}\)，不太重要，随便算一下。

monkfish / anglerfish

task.py 太长了，不贴了

没看懂这题想干啥，，，有点搞笑，还分了两题

题目里给出了一个看起来很复杂的线性代数的算法，但是实际上都不重要，因为我们关注一下 \(verify(v, F, pok = (com, resp, verif))\) 函数，大概是用输入的 \((com, v, verif)\) 三元组为随机数种子随机一个 \(a\)，然后判断 \(apply(F, resp) = com + a^2 v - a \cdot verif\)。但是所有数都是 \(\bmod 5\)，意味着实际上 \(a\) 是可能随机到 \(0\) 的，而如果 \(a = 0\) 的时候这个判断条件是很容易满足的，只需要 \(com = apply(F, resp)\)，而 \(com, resp\) 都是我们输入的，只需要随机一个 \(resp\) 并确定对应的 \(com\)，为了随机到 \(a=0\) 我们一直对 \(verif\) 进行随机就行了。

#!/usr/bin/sage

import sys
print("I caught a monkfish in the sea! ")
sys.stdout.flush()

from hashlib import sha256
from Crypto.Util.number import bytes_to_long
from random import SystemRandom
import ast

n = 100
m = 100
q = 5
FF.<x> = GF(q)


def apply(F, v):
    out = []
    for i in range(m):
        out.append((v.T * F[i] * v)[0, 0])
    return matrix(FF, m, 1, out)

def apply_verif_info(F, a, b):
    out = []
    for i in range(m):
        out.append((a.T * (F[i] + F[i].T) * b)[0, 0])
    return matrix(FF, m, 1, out)

def create_pok(v, s, F):
    t = matrix(FF, n, 1, [FF.random_element() for i in range(n)])
    com = apply(F, t)
    verif = apply_verif_info(F, t, s)
    a = list(FF)[sha256(bytes([list(FF).index(i[0]) for i in list(com) + list(v) + list(verif)])).digest()[0] % len(list(FF))]
    print("a =", a)
    return (com, t - a * s, verif)

def verif_pok(v, F, pi):
    com = pi[0]
    resp = pi[1]
    verif = pi[2]
    a = list(FF)[sha256(bytes([list(FF).index(i[0]) for i in list(com) + list(v) + list(verif)])).digest()[0] % len(list(FF))]
    out1 = apply(F, resp)
    out2 = com + (a * a) * v - a * verif
    return out1 == out2

gen_seed = bytes([83, 134, 8, 60, 109, 129, 153, 246, 112, 132, 154, 0, 129, 173, 49, 229, 71, 79, 145, 91, 146, 44, 34, 251, 95, 41, 13, 248, 24, 126, 215, 95, 208, 88, 24, 74, 224, 166, 19, 232, 254, 0, 142, 215, 146, 93, 87, 249, 239, 253, 137, 92, 124, 201, 164, 4, 133, 176, 76, 70, 166, 193, 68, 148])

F = []

for i in range(m):
    cur = []
    for j in range(n):
        cur.append([])
        for k in range(n):
            cur[-1].append(list(FF)[sha256(gen_seed).digest()[0] % len(list(FF))])
            gen_seed = sha256(gen_seed).digest()
    F.append(matrix(FF, n, n, cur))

vl = [2, 0, 3, 2, 4, 2, 4, 1, 4, 3, 4, 1, 1, 1, 2, 0, 4, 3, 4, 0, 0, 0, 0, 3, 2, 2, 3, 2, 0, 1, 1, 4, 2, 3, 4, 2, 4, 4, 2, 0, 1, 0, 1, 3, 4, 0, 0, 1, 0, 3, 4, 3, 0, 3, 4, 1, 1, 4, 1, 3, 0, 1, 4, 1, 2, 2, 2, 3, 2, 2, 4, 2, 4, 3, 0, 0, 3, 1, 4, 2, 1, 2, 1, 3, 2, 3, 4, 4, 4, 0, 1, 1, 2, 2, 1, 4, 3, 0, 2, 4]

v = matrix(FF, n, 1, [list(FF)[i] for i in vl])

m1 = random_matrix(FF, n, 1)
m0 = apply(F, m1)
while True:
    m2 = random_matrix(FF, n, 1)
    a = sha256(bytes([list(FF).index(i[0]) for i in list(m0) + list(v) + list(m2)])).digest()[0] % len(list(FF))
    print("a =", a)
    if a == 0:
        pi = (m0, m1, m2)

        res = verif_pok(v, F, pi)
        assert res == True
        print([list(FF).index(i[0]) for i in list(m0)])
        print([list(FF).index(i[0]) for i in list(m1)])
        print([list(FF).index(i[0]) for i in list(m2)])
        exit()
    

CrewCTF 2024

这场是接着上一场打的，时间不多了所以排名不好看。上一场没有什么很有趣的 crypto 题，几个古典密码，一个很无聊的题和一个抄的攻击实现，所以没啥可写的。有一个椭圆曲线题，为此我还去学了下，但是最后也没做出来。结果最后发现正解是爆破，他妈的弱智。（大概有一个普通的离散对数还有一个椭圆曲线离散对数，两部分解决方案都是爆破，什么玩意）

read between the lines

task.py:

#!/usr/bin/env python3

from random import shuffle
from Crypto.Util.number import getPrime

from secret import FLAG

assert len(FLAG) < 100

encoded_flag = []

for i, b in enumerate(FLAG):
    encoded_flag.extend([i + 0x1337] * b)

e = 65537
p, q = getPrime(1024), getPrime(1024)
n = p * q

c = sum(pow(m, e, n) for m in encoded_flag) % n

with open('output.txt', 'w') as f:
    f.write(f'{n = }\n{e = }\n{c = }\n')

挺简单的题其实是，分析一下容易发现 \(c\) 的表达式是 \(\sum_i f_i (1337+i)^e\)，这玩意看起来很恐怖，实际上后面就是一个关于 \(i\) 的常量，看作是解 \(c \equiv \sum_i f_i a_i \pmod n\) 就行了，然后直接上个 LLL 解背包就能过了。

题外话：我真的应该把我古老的 NOI Linux 2.0（Ubuntu 20.04）扔掉重新装一个 22.04 或者装个 kali 了，由于 20.04 上没有新版本的 sage，而自己装好像只能从 conda 装，我还不太会用这个（主要是我需要之前装过的很多 py 库，我也不会迁移这个而且我真没用过 venv 之类的），所以直接装了 apt 上的旧版本，结果旧版本上没有很多格基相关功能，我又不会自己调参，，于是写好了找了个在线 sage 跑的，很火大

n = 11570808501273498927205104472079357777144397783547577003261915477370622451850206651910891120280656785986131452685491947610185604965099812695724757402859475642728712507339243719470339385360489167163917896790337311025010411472770004154699635694228288241644459059047022175803135613130088955955784304814651652968093606122165353931816218399854348992145474578604378450397120697338449008564443654507099674564425806985914764451503302534957447420607432031160777343573246284259196721263134079273058943290282037058625166146116257062155250082518648908934265839606175181213963034023613042840174068936799861096078962793675747202733
e = 65537
c = 7173375037180308812692773050925111800516611450262181376565814072240874778848184114081029784942289615261118103256642605595499455054072839201835361613983341298973366881719999836078559255521052298848572778824157749016705221745378832156499718149327219324078487796923208917482260462508048311400560933782289383624341257636666638574026084246212442527379161504510054689077339758167386002420794571246577662116285770044542212097174474572856621921237686119958817024794843805169504594110217925148205714768001753113572920225449523882995273988088672624172009740852821725803438069557080740459068347366098974487213070886509931010623

from sage.modules.free_module_integer import IntegerLattice

for len in range(1, 100):
    print("ckecking", len)
    a = matrix(ZZ, len + 1, len + 1)
    M = 1000
    for i in range(len):
        a[i, i] = 1
        a[i, len] = pow(0x1337 + i, e, n) * M
    a[len, len] = n * M

    a = IntegerLattice(a)
    vec = a.approximate_closest_vector([0] * len + [c * M])

    if vec[len] != c * M:
        continue
    flag = True
    for i in range(len):
        if vec[i] < 0 or vec[i] >= 256:
            flag = False
            break
    if flag:
        for i in range(len):
            print(chr(vec[i]), end='')
        print()
        exit()

CTFZone 2024 Quals

cool

一个资格赛，可能难度相对来说比较高，还能过一些题不错了！

Shes the Real one

task.py:

from functools import namedtuple

from secret import flag

assert len(flag) == 33

Point = namedtuple("Point", ["x", "y"])
R = RealField(prec=800)
inf = Point(R(0), R(1))


def lift_x(x):
    return Point(x, sqrt(x**3 - R(3) * x - R(2)))


def add(P, Q):
    if P.x == Q.x and P.y != Q.y:
        return inf
    elif P.y == Q.y:
        raise ValueError("Points have to differ!")
    elif P == inf:
        return Q
    elif Q == inf:
        return P

    lambda_ = (P.y - Q.y) / (P.x - Q.x)

    xr = lambda_**2 - P.x - Q.x
    yr = lambda_ * (Q.x - xr) - Q.y
    return Point(xr, yr)


def double(P):
    if P == inf:
        return P

    lambda_ = (R(3) * P.x**2 - R(3)) / (R(2) * P.y)

    xr = lambda_**2 - 2 * P.x
    yr = lambda_ * (P.x - xr) - P.y
    return Point(xr, yr)


def multiply_by_scalar(P, n: int):
    if n == 0 or P == inf:
        return inf
    elif n < 0:
        return multiply_by_scalar(Point(-P.x, P.y), -n)

    R0, R1 = P, double(P)
    for b in bin(n)[3:]:
        if b == "0":
            R0, R1 = double(R0), add(R0, R1)
        else:
            R0, R1 = add(R0, R1), double(R1)
    return R0


P = lift_x(R(5.0) + R.random_element())
s = int.from_bytes(flag, 'big')
Q = multiply_by_scalar(P, s)
with open("output.dump", 'wb') as f:
    f.write(dumps([P, Q]))

应该算是一个基础椭圆曲线题？由于上一场研究过很多椭圆曲线相关的攻击，这次很快就找到了突破口。

首先从 lift_x 中可以得到椭圆曲线的表达式：

\[y^2 = x^3 - 3x - 2 \]

这个系数看着就很小啊！可以用一些基础的测试方法测试一下这个系数，反正很容易可以发现这个东西其实是可以因式分解的：

\[y^2 = (x+1)^2(x-2) \]

把曲线平移一下即可得到一个很简单的形式：

\[y^2 = x^2 (x-3) \]

这是一个非常经典的可以被攻击的椭圆曲线，如果一个椭圆曲线后面的多项式存在重根则可以攻击。\(y^2 = x^3\) 的形式是最简单的，\(y^2 = x^2(x+a)\) 也是可以破解的。具体来说，对于前者，可以通过映射 \(E(x, y) \to \frac{x}{y}, \infty \to 0\) 得到一个加法群，然后椭圆曲线离散对数问题就非常容易解决了（就是一个除法）。对于后者，可以通过映射 \(E(x, y) \to \frac{x + \sqrt{a} y}{x - \sqrt{a} y}, \infty \to 1\) 得到一个乘法群，然后椭圆曲线离散对数问题就变成了一个普通的离散对数问题，相对来说要容易解决一些。

这题是后者的情况，而我们的 \(a=-3\)，也就是说我们需要映射到复数上了。容易发现映射后的复数模长为 \(1\)，我们得到两个复数 \(a, b\)，我们就是要找一个 \(f\) 使得 \(a^f = b\)，取一下辐角即可得到 \(\alpha f = b + 2\pi n\)，其中 \(n\) 是一个正整数。我们可以看作是 \(\alpha f \equiv b \pmod {2\pi}\)，这就是一个线性同余了，由于小数位数很多，我们乘一个 \(2^900\) 然后取整后转换到整数上做，然后直接无脑上 LLL 就行了。我不知道这种只有一个变量的要怎么解啊，有没有老哥教教，反正 LLL 能出。approximate_closest_vector 真的好用啊。

from functools import namedtuple
from Crypto.Util.number import *

Point = namedtuple("Point", ["x", "y"])
R = RealField(prec=800)
inf = Point(R(0), R(1))

C = ComplexField(prec=800)

with open("output.dump", 'rb') as f:
    P, Q = loads(f.read())

print(P, Q)

def f(p):
    x = p.x
    y = p.y
    x += 1
    return C(y, sqrt(3) * x) / C(y, -sqrt(3) * x)

p = f(P)
q = f(Q)

a = imag(log(p))
b = imag(log(q))

# solve fa = b (mod 2pi)

M = 2 ** 264
N = 2 ** 800

A = Matrix(ZZ, [
    [floor(a * N), 1],
    [floor(2 * pi * N), 0]
])

from sage.modules.free_module_integer import IntegerLattice

B = IntegerLattice(A)

print(long_to_bytes(B.approximate_closest_vector([floor(b * N), M])[1]))

Cold Siemens

我最一开始先开的这个，可能开场没用很长时间就做出来了？但是一开始网站上的 flag 放错了，导致一开始一直 0 solve，等恢复了之后我交上之后就有 2 solves 了，我不知道我到底是不是一血，因为一开始网站都有问题。

task.py:

import os
import random
from math import log

from Crypto.Util.number import long_to_bytes
from gmpy2 import iroot

from secret import flag

TARGET_LEN = 666
left_pad = random.randint(TARGET_LEN // 3, TARGET_LEN // 2)
right_pad = TARGET_LEN - left_pad - len(flag)
flag = os.urandom(left_pad) + flag + os.urandom(right_pad)


def sqrsqr(x: int, prec: int) -> tuple[int, int]:
    return int(iroot(x * 10 ** (prec * 4), 4)[0]) % 10**prec


class Server:
    def __init__(self, bl: int, skip: int = 1000):
        self.bl = bl
        self.K = random.randrange(0, 2**self.bl)
        self.cipher = None
        self.key = None
        random.seed(self.K)

    def init_cipher(self, keylen: int):
        alpha = sqrsqr(self.K, prec=keylen)
        alpha_list = list(str(alpha).zfill(keylen))
        random.shuffle(alpha_list)
        self.key = long_to_bytes(int("".join(alpha_list)))

    def encrypt(self, m: bytes) -> bytes:
        keylen = round(log(10 ** len(m)) / log(10))
        self.init_cipher(keylen)
        sc = (len(m) + len(self.key) - 1) // len(self.key)
        return bytes([x ^ y for x, y in zip(m, self.key * sc)])


S = Server(bl=256)

print("Encrypted flag: ", S.encrypt(flag).hex())
while True:
    try:
        msg = bytes.fromhex(input("m: "))
        if len(msg) > 285:
            print("Message to big to encrypt, sorry")
        else:
            print("Encrypted msg: ", S.encrypt(msg).hex())
    except Exception as e:
        print(e)
        exit()

首先注意到这是一个异或加密，而且我们可以自己输入明文得到密文，所以 key 是很容易获取的。key 是某个东西的重复，可以简单寻找一下最小循环节来得到这个 key，然后分析一下 key 是什么。可以发现 key 是 \(\sqrt[4]{K}\) 的 \(n\) 位小数部分 shuffle 得到的，而 shuffle 所用的 seed 也是 \(K\)，所以如果我们能还原出 \(K\) 来实际上也就能够得到 key 从而解出 flag 了。

可以拿程序跑出来 \(285\) 位 \(\sqrt[4]{K}\) 的小数部分，现在问题就是给出 \(\sqrt[4]{K}\) 的小数部分从而还原 \(K\)。哈哈这个我有经验啊！这篇博最开头就是个三次根号的题，用一模一样的做法就能解出来了。

获取小数部分：

from Crypto.Util.number import *
from pwn import *
from math import *

# io = process([ 'python3', 'task.py' ])
io = remote('cold_siemens.ctfz.zone', 1188)

# context.log_level = 'debug'

f = log10(256)

flag = io.recvline()[len('Encrypted flag:  '):].strip()

print("flag:", flag)

d = 0
lst = []

for x in range(1, 286):
    # print("digit", x)
    io.sendlineafter(b'm: ', b'00' * x)
    ori = bytes([0] * x)
    now = bytes.fromhex(io.recvline()[len('Encrypted msg:  '):-1].decode())
    key = bytes([x ^ y for x, y in zip(ori, now)])
    keylen = max(1, int(floor(x / f)) - 1)
    while keylen < len(key) and key[0] != key[keylen]:
        keylen += 1
    if x > 10:
        while keylen < len(key) and key[0 : 2] != key[keylen : keylen + 2]:
            keylen += 1
    key = key[:keylen]
    key = list(str(bytes_to_long(key)).zfill(x))
    cc = 0
    for i in key:
        if lst.count(i) > 0:
            lst.remove(i)
        else:
            d = d * 10 + int(i)
            # print(i)
            cc += 1
    if cc != 1:
        print("error")
        break
    lst = key

m = 285

print('d:', d)

求解 \(K\) 部分：

d = 0.552614595204287979807856154939042235218477194309748799957420905710149800055341805019514376906258499559095896775423817284550380575486264184700632183171344936543190111597307051093409215284141322557986592334377958046723110960896879684591934100408184702751852343915234092895045700941304497
M = 2 ** 64
N = 2 ** 900

A = matrix(ZZ, [
    [floor(4 * N * d), 1, 0, 0],
    [floor(6 * N * d * d), 0, 1, 0],
    [floor(4 * N * d * d * d), 0, 0, 1],
    [N, 0, 0, 0]
])


from sage.modules.free_module_integer import IntegerLattice

B = IntegerLattice(A)
a = B.approximate_closest_vector([-floor(d * d * d * d * N), M ** 3, M ** 2, M])


t1 = a[1]
t2 = a[2]
t3 = a[3]
print(-floor(d * d * d * d * N))
print(a[0])
print(t2)
print(t3 * t3)
print(round((t3 + d) ** 4))

解 flag 部分：

import os
import random
from math import log

from Crypto.Util.number import long_to_bytes
from gmpy2 import iroot

# from secret import flag
flag = b'CTFZone{test}'

TARGET_LEN = 666
left_pad = random.randint(TARGET_LEN // 3, TARGET_LEN // 2)
right_pad = TARGET_LEN - left_pad - len(flag)
flag = os.urandom(left_pad) + flag + os.urandom(right_pad)


def sqrsqr(x: int, prec: int):
    return int(iroot(x * 10 ** (prec * 4), 4)[0]) % 10**prec


class Server:
    def __init__(self, bl: int, skip: int = 1000):
        self.bl = bl
        self.K = 60524391950962576960088028569211737700220255699569156977377615495035094550061
        self.cipher = None
        self.key = None
        random.seed(self.K)

    def init_cipher(self, keylen: int):
        alpha = sqrsqr(self.K, prec=keylen)
        alpha_list = list(str(alpha).zfill(keylen))
        random.shuffle(alpha_list)
        self.key = long_to_bytes(int("".join(alpha_list)))

    def encrypt(self, m: bytes) -> bytes:
        keylen = round(log(10 ** len(m)) / log(10))
        # print("keylen:", keylen)
        self.init_cipher(keylen)
        # print("key:", self.key)
        # print("actkey:", len(self.key))
        sc = (len(m) + len(self.key) - 1) // len(self.key)
        return bytes([x ^ y for x, y in zip(m, self.key * sc)])



S = Server(bl=256)

flag = bytes.fromhex('d6749e60b10ff44cc575a7512fa345b51dba614aaaeb46d57bf079cbf5ce6cfe5da50e88cf7856da590beaf410bb76795ce160938622a3fa9ce644a6795db315d45205027bf8e40709be30e357a6004edf7db41997af52b48fc73ac96aa68f5eccfa1240ba39dbbdae01ce1eade83fa916fe9351b7830b46cdba14bd8b03096bd6a3f82f04419879b0d13df4bc9accc0846fc9938278f56bf548fbe60fe47c408316d9f14a30361553e7472bdefb0d01ace8b0770e7a390a87802ea2da82a0242228646c1dc6e67aed74724601dfb7260a07a4af7576cacebfb23a737d80561bc604be067d940729fed3d91b58aa0ec1331740cf3d657ed659dee5c9f8a07762a36864d1923d9baf9fa8695cc3ca03e4393d8020d362e98d3c683bf333b979f5f3b1280d75d5b596a2fdd0f2a1b92259ca28dbed537a9091c4f4b2c78d0ee6bcbfb9be83603c0116feb10b56825371b61dc0cc002b530bf5bbb276810dd9eddfb6805fcf7dd7fd898013b14bb67e64a90331c46a98adb1b722c39449117272e365fb5a59b3305a10c3bbd5f7bf8b9c40d0ba8549ceadc0b90e5d6352787c45ba005be7537db4f54bc3ecb2f8669f0525c3f0c190792529ee6a57568c470465b74be211ebe23745c382727bc76ae166f753e12eb6ea3a43a1b2350ff87713649cacb71d518936350d07aad1e7ff410c869f7b5ca8a886024137d2944be7e929432a49a81ae440bad0e38e2f7937bec45b802c284813f746ce232933e162d9c59412f5230bc113bd1adefa10733b7537e9168af6524516dc8b7ce825a322a69665bd39f7fadcc88d4ee0035d8c7c5a361f18cac63556ff8a1e379ee20057eb0bff8925f92d92aee7ae33da483dfca857317657823ed1526f71b430134d8a3f55cb4c0144d4942da9b40fcf182588113ab21dc6a7246f7c8abda215')

print(S.encrypt(flag))

LITCTF 2024

好耶。

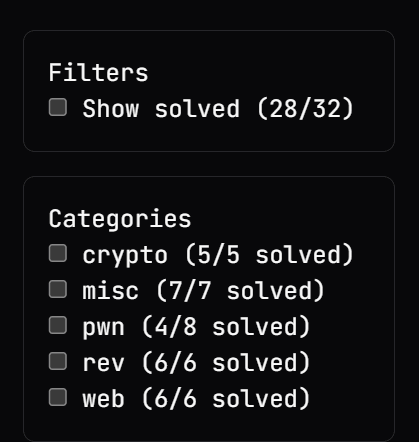
相对来说要简单一些的比赛，不过也没有特别简单，能把除了 pwn 的全 ak 了还是很爽的！

Symmetric RSA

task.py

#!/usr/bin/env python3
from Crypto.Util.number import long_to_bytes as ltb, > bytes_to_long as btl, getPrime

p = getPrime(1024)
q = getPrime(1024)

n = p*q

e = p

with open("flag.txt", "rb") as f:
	PT = btl(f.read())

CT = pow(PT, e, n)
print(f"{CT = }")

for _ in range(4):
	CT = pow(int(input("Plaintext: ")), e, n)
	print(f"{CT = }")

一个常规的 rsa，只不过 \(e = p\)。

首先我们可以进行四次自己询问，我们只有一个密文，连 \(n\) 都没有，所以得先拿到 \(n\)。这个是好搞的，考虑问出来三个密文 \(2^p, 4^p, 16^p\)，容易发现后者是前者的平方，这样我们很容易得到前者平方减去后者是 \(n\) 的倍数，两个差求一下 \(\gcd\) 就得到 \(n\) 了。

拿到 \(n\) 之后还剩下一个问题：如何找到 \(p\)。很容易想到 \(m^p \equiv m \pmod p\)，但是我们此时只能得到 \(m^p \pmod {n=pq}\)，不过不要紧，这个数的基础上我们模 \(p\) 就能得到前者了，而我们知道前者等于 \(m\)，所以这说明 \(m^p \bmod n = m + k \cdot p\)。这是一个很重要的信息，这样我们只需要把每个询问出来的数减去 \(m\) 再求一下 \(\gcd\) 就能得到 \(p\) 了，然后就能解掉这个 rsa 了。

from pwn import *
from math import gcd
from functools import reduce
from Crypto.Util.number import *
# io = process(['python3', 'chall.py'])
io = remote('litctf.org', 31783)
flag = int(io.recvline()[len('CT = '):])

io.sendlineafter(b'Plaintext: ', b'2')
x = int(io.recvline()[len('CT = '):])
io.sendlineafter(b'Plaintext: ', b'4')
y = int(io.recvline()[len('CT = '):])
io.sendlineafter(b'Plaintext: ', b'16')
z = int(io.recvline()[len('CT = '):])
io.sendlineafter(b'Plaintext: ', b'256')
w = int(io.recvline()[len('CT = '):])

n = reduce(gcd, [x * x - y, y * y - z, z * z - w])

p = reduce(gcd, [x - 2, y - 4, z - 16, w - 256])

assert n % p == 0

q = n // p

d = inverse(p, (p - 1) * (q - 1))

print(long_to_bytes(pow(flag, d, n)))

Truly Symmetric RSA

搞笑的事情：有人过了这题之后将分解出来的 p 和 q 传到了 factordb 上，导致这题通过比上一题还高，尽管这题是上一题的加强版。

task.py

#!/usr/bin/env python3
from Crypto.Util.number import long_to_bytes as ltb, > bytes_to_long as btl, getPrime

p = getPrime(1536)
q = getPrime(1024)

n = p*q

e = p

with open("flag.txt", "rb") as f:
	PT = f.read()

CT = pow(btl(PT), e, n)
print(f"{len(PT) = }")
print(f"{CT = }")
print(f"{n = }")

和上一题基本一样，只不过这次没有自己询问的机会了。倒是给出了 \(n\)。

那么我们就需要另外找方法了。从上一题可以搬过来的东西是 \(CT = flag + k \cdot p\)，一种想法是通过某种方式求 \(\gcd(n, CT - flag) = p\)，似乎 discord 上有人说从这里开始暴力对多项式跑 gcd 然后把中间过程多项式拿出来解一解能解出来？我反正没能这么过。

再注意一下 \(CT = flag + k \cdot p\)。这个式子不是很好处理，原因是后面有两个未知量乘积。不过我们知道的是 \(flag\) 是要远远小于 \(CT\) 和 \(n\) 的，也许可以利用这一点。考虑给式子除以一个 \(n\)，得到 \(\frac{CT}{n} = \frac{flag}{n} + \frac{k}{q}\)，这个形式就完美了，注意到 \(\frac{flag}{n}\) 是很小的，所以 \(\frac{CT}{n} \approx \frac{k}{q}\)。那么我们只需要对 \(\frac{CT}{n}\) 找一个有理分式逼近即可找到 \(k\) 和 \(q\) 了，进而解决这题。

好像还有 LLL 的做法？我不会了

from Crypto.Util.number import *

CT = 155493050716775929746785618157278421579720146882532893558466000717535926046092909584621507923553076649095497514130410050189555400358836998046081044415327506184740691954567311107014762610207180244423796639730694535767800541494145360577247063247119137256320461545818441676395182342388510060086729252654537845527572702464327741896730162340787947095811174459024431128743731633252208758986678350296534304083983866503070491947276444303695911718996791195956784045648557648959632902090924578632023471001254664039074367122198667591056089131284405036814647516681592384332538556252346304161289579455924108267311841638064619876494634608529368113300787897715026001565834469335741541960401988282636487460784948272367823992564019029521793367540589624327395326260393508859657691047658164
n = 237028545680596368677333357016590396778603231329606312133319254098208733503417614163018471600330539852278535558781335757092454348478277895444998391420951836414083931929543660193620339231857954511774305801482082186060819705746991373929339870834618962559270938577414515824433025347138433034154976346514196324140384652533471142168980983566738172498838845701175448130178229109792689495258819665948424614638218965001369917045965392087331282821560168428430483072251150471592683310976699404275393436993044069660277993965385069016086918288886820961158988512818677400870731542293709336997391721506341477144186272759517750420810063402971894683733280622802221309851227693291273838240078935620506525062275632158136289150493496782922917552121218970809807935684534511493363951811373931

l = (0, 1)
r = (1, 0)

def check(q1, q2):
    if q2 > 1 and n % q2 == 0:
        q = q2
        p = n // q
        d = inverse(p, (p - 1) * (q - 1))

        print(long_to_bytes(pow(CT, d, n)))
        exit()

while True:
    mid = (l[0] + r[0], l[1] + r[1])
    check(mid[0], mid[1])
    if mid[0] * n < CT * mid[1]:
        l = mid
    else:
        r = mid