NOI 2024 前做题纪要

快退役了，最后一集了

退役前还能做多少呢

To-do list #3

目录

2024.5.24

AGC025D Choosing Points

讲过

关键性质是距离 \(\sqrt{d}\) 的点为二分图，于是每次选二分图较大的一边即可做到 \(n^2\)。

证明：考察 \((x_1 - x_2)^2 + (y_1 - y_2)^2 = d\) 奇偶性，\(d\) 为奇数时 \(x_1 - x_2\) 和 \(y_1 - y_2\) 一奇一偶，则 \(x_1 - y_1\) 与 \(x_2 - y_2\) 一奇一偶，直接可以按照 \(x_1 - y_1\) 奇偶性划分二分图。\(d\) 为偶数时，考察其 \(\bmod 4\) 的值，若 \(d \bmod 4 = 2\)，则发现一定有 \(x_1 - x_2\) 和 \(y_1 - y_2\) 都是奇数，此时 \(x_1\) 与 \(x_2\) 奇偶性不同，\(y_1\) 与 \(y_2\) 奇偶性不同，可以划分二分图。否则，可以将 \(x_1, x_2, y_1, y_2\) 除以 \(2\)，\(d\) 除以 \(4\)，然后可以规约到前面的情况。

P9531 [JOISC2022] 复兴计划

想不到题解做法

注意到一条边存在的宽度是一段区间，考虑求出这段宽度，然后就好做了。

考察一个宽度 \(t\) 能不能包含第 \(i\) 条边，那么我们就是将小于 \(|t - w_i|\) 的所有边加入后，然后看第 \(i\) 条边是否能加上，我们钦定边权相同的先加左边再加右边，那么注意到小于 \(|t - w_i|\) 的所有边一定形成一个以 \(w_i\) 为右端点的后缀（或以 \(w_i\) 为左端点的前缀），那么我们可以直接枚举这个前缀或后缀，看看能不能加入，然后再计算最小或最大的宽度即可，这立即得到了一个 \(O(m^2 \alpha(n))\) 的做法。注意到 \(n\) 比较小，所以我们可以尝试找出有用的 \(n\) 条边，也就是对于一个前缀，从后往前依次加入得到的生成树，这可以直接从前往后依次加边维护出来，如果不连通则直接把这个边加上，否则就把路径上宽度最小的删除，这样就能维护出每个前缀得到的生成树了。

总复杂度 \(O(nm \alpha + m \log n)\)。但是这个做法好像没法优化到 \(O(m(\log n + \log m) + m \log n)\)。

没脑子，想了一上午加下午半个多小时

题解做法太深刻了，就是考虑直接从大到小加入每条边，然后考察这条边能被加入的条件，假如加入 \(w\) 时路径上边权最大的边是 \(w'\)，那么当 \(x < \frac{w + w'}{2}\) 时当前边可以加入，否则不能加入，根据此可以得出每条边加入的区间。

AGC021D Reversed LCS

这啥啊，这咋紫的

注意到一定选回文子序列，直接 DP 即可，复杂度 \(O(n^3)\)。

2024.5.25

vp 了一些 pkusc

太深刻了

PKUSC 2024 D1T1

枚举个回文中心 manacher 然后二分个哈希就行了，没写

PKUSC 2024 D1T2

不知道有没有更简单的做法，口胡的，好像有人这么写过了，所以应该可行

先枚举一个正方形中点到一个角的向量，正方形在凸多边形内就是四个角在凸多边形内，于是满足条件的中点就是满足这个点加四个方向的向量都在凸多边形内的整点（或者是 \(\frac{1}{2}\) 一类的东西吧），然后可以把凸多边形沿这四个方向移动一下取个交，得到的新凸多边形就是中点可以在的位置，然后统计凸多边形内整点就行了。因为交完之后凸多边形可能不是格点凸多边形，所以可能需要类欧统计整点啥的。

这我写个屁。

PKUSC 2024 D1T3

只会 48 分暴力

肯定 DP 套 DP 一类的，考虑朴素 DP：

\[\begin{aligned} f_{u, 0} &= \sum_{v \in s_u} \max(f_{v, 1}, f_{v, 0})\\ f_{u, 1} &= a_u + \sum_{v \in s_u} f_{v, 0} \end{aligned} \]

直接对这个做肯定太差了，考虑某种方式把贡献拆开，那就瞎变换一会，考虑 \(f_{u, 1} - f_{u, 0}\)：

\[f_{u, 1} - f_{u, 0} = a_u - \sum_{v \in s_u} \max(0, f_{v, 1} - f_{v, 0}) \]

发现具有良好的形式，令 \(g_u = max(0, f_{u, 1} - f_{u, 0})\)，则有 \(g_u = \max(0, a_u - \sum_{v} g_v)\)。同时注意到 \(f_{u, 0} = \sum_v f_{v, 0} + g_v\)，那么可以得到 \(\max(f_{1, 0}, f_{1, 1}) = \sum g_u\)，那么就把贡献拆开了，且每个 \(g_u\) 值域只有 \(m\)，可以 \(O(nm^2)\) DP 了。这个东西的大致意义就是从下到上考虑每个点选比不选会多出多少贡献，然后求和就是答案。

优化不会。好像是可以推一通发现答案的生成函数一定满足 \(G_u(x) = \frac{F_u(x)}{(1-x)^{siz_u}}\)，其中 \(F_u(x)\) 是一个 \(siz_u\) 次多项式，然后信息量只有 \(O(n)\) 了，推一下咋转移的好像就行了，好像还要研究怎么把多项式模 \(x^{m+1}\)，太困难了我摆了。

PKUSC 2024 D2T1

考虑依次维护每个前缀复原所需的操作次数与复原后对剩下的后缀的操作序列。注意到交换相邻两个操作不会使得局面改变，所以可以直接维护对每个点操作了多少次，每次从 \([1, i]\) 拓展到 \([1, i + 1]\)，考虑 \(i+1\) 是否能还原，如果此时 \(i+1\) 操作了奇数次则不能，需要再进行一轮，将所有操作全部乘 \(2\) 即可，然后偶数就直接操作，把操作次数平分到两个后继。可以通过一些打 tag 操作优化到 \(O(n)\) 次操作，然后需要高精度，压位高精即可做到 \(O(\frac{n^2}{w})\)。

PKUSC 2024 D2T2

我的 \(O(n \log^2 n)\) 做法：注意到复合函数是单调的，所以 \(n\) 个函数复合只有 \(O(n)\) 段，可以直接线段树维护复合函数，单次复合可以做到 \(O(n)\) 或 \(O(n \log n)\)，线段数每一层总段数是 \(O(n)\) 的，所以线段树可以 \(O(n \log n)\) 或 \(O(n \log^2 n)\) 建树，然后查询直接依次查询每个区间的分段函数，\(O(q \log^2 n)\) 可以实现。

正解：这函数形式太优美了，就是一个值域区间 \(+1\)，操作完后大小关系不会改变，所以直接拿个数据结构维护当前所有询问，然后对函数扫描线直接模拟即可 \(O(n \log n)\)。

PKUSC 2024 D2T3

不会。

P7563 [JOISC 2021 Day4] 最悪の記者 4 (Worst Reporter 4)

首先是基环树，分别计算每一个连通块的答案，显然环上全部相等，然后树部分可以树形 DP 一下，设 \(f_{u, i}\) 表示 \(u\) 点的点权 \(\le i\) 的最小代价，然后 DP 就是修改当前点权，把所有儿子加起来之后再全部加 \(c_u\)，或者不修改点权，然后做一个后缀 \(\min\)。注意到是单调的，所以后缀 \(\min\) 可以二分一下拆掉改成区间覆盖。

那么现在要维护的操作就是区间覆盖，全局加，合并。可以线段树合并来做，由于涉及到区间操作，线段树合并需要注意当一个点被区间操作后需要特殊处理才能保证复杂度。

具体来讲，我们可以对每个节点维护当前区间是否全部等于某个值，或者这个区间的加法标记，加法标记可以直接下传，区间赋值的时候需要把区间等于某个值的标记下传。合并的时候先看看其中两个子树是否存在全部等于某个值的点，如果有就给另一棵子树打一个加法标记，这样就避免了递归下去新建节点，线段树合并的复杂度就对了。

复杂度 \(O(n \log n)\) 或 \(O(n \log^2 n)\)，看二分怎么写的。我比较懒直接暴力二分了。

好像也可以直接维护区间 \(\min\) 的标记，感觉有点混乱就改成区间赋值了。

2024.5.26

昨晚打了 cf，把分上回来了，终于回红了，感动了。

赛时想到了 G 题怎么做了，不过我想的做法常数有点太大了导致赛时被卡常了 ;-;

上午有场模拟赛。感觉诡异，不知道要不要写。反正是空间爆了+卡常卡 WA 了+卡常了，哈哈。T1 并没有很理解，5k 给出了一个很神秘的条件，我感觉完全没啥对的道理，但是确实过了而且拍不掉，不懂了

CF1975G Zimpha Fan Club

考虑分几种情况讨论：

  • 两个串都没有 *：这个很好判断，\(O(n)\) 扫一遍即可；
  • 两个串都有 *：注意到 * 之内的所有内容都是容易被另一个串的 * 匹配的，所以我们只需要满足开头和结尾能够被匹配上，也是扫一遍即可；
  • 一个串有 * 一个串没有 *。

我们现在只考虑第三种情况，钦定 \(T\) 串是有 * 的那个串。那么问题相当于，将 \(T\) 串按照 * 划分开后，每一段要匹配到 \(S\) 上的一部分，问能否匹配。贪心地考虑，我们每次找到这个串在 \(S\) 中的第一次匹配位置，并把它在这里匹配上即可。带通配符的匹配是经典的，参考 残缺的字符串。但是我们并不能每次都把整个 \(S\) 与 \(T\) 匹配，否则复杂度变成 \(O(n^2 \log n)\) 了。但是我们只需要找到最靠前的匹配位置，所以可以考虑每次只尝试匹配一小段。具体的，我们每次将 \(T'\) 串与 \(S\) 串的长为 \(2|T'|\) 的前缀进行匹配，如果不能匹配则删去一个长为 \(|T'|\) 的前缀。然后这样复杂度就做到 \(O(n \log n)\) 了。

我赛时想法是直接倍增找能匹配的第一个位置，这样也是 \(O(n \log n)\) 的，但是有两倍或更大的常数，然后就爆炸了，呃呃

2024.5.27

膜拜 happyguy

happyguy：我往简单里出的，但是看来大家好像都不太会

happyguy：看来大家都没做过凸包的题

T1 思考到了大概九点会了，然后想了一会实现细节感觉巨大难写，不觉得自己能写完点分治（那个傻逼 I 之后我都不敢写点分了，觉得这玩意至少写 2h+），然后先看 T2，结果把 T2 题看错了想了半天，，T3 交互，被大家薄纱了，呃呃了 然后还写了 T2 假做法，写完之后发现贪心假了，结果下午得知是凸包，我只需要把我的单调栈改成凸包就做完了，，，是不是之前有一个题也是找了个单调栈然后假了然后结果做法是凸包，流汗了

QOJ2070 Heavy Stones

每堆石子只会被合并一次，先把这个贡献计算掉。然后就是考虑每个点要被合并多少次，显然如果第 \(i\) 堆合并的石子会被合并 \(n - i\) 次，那么问题就变成了，每次选左边或者右边的一个数，然后给其赋 \(n-i\) 的系数，使得和最小。考虑某一种操作序列，按照在左边选或者在右边选划分成若干连续段。我们考虑相邻两端能否交换使得答案更优，即假如有相邻两端长度分别为 \(n, m\)，权值分别为 \(a_i, b_j\) 的序列，比较 \(\sum_{i=1}^n -i a_i + \sum_{i=1}^m -(i+n) b_i\) 与 \(\sum_{i=1}^m -i b_i + \sum_{i=1}^n -(i+m) a_i\) 的大小关系，相减即可发现这等价于比较两个序列的平均数。那么我们实际上就是要求每一段的平均数递增，平均数相当于二维平面上的点 \((i, \sum a_i)\) 的斜率，于是我们要做的实际上就是对这个东西求凸包。

那么对前缀维护出一个凸包，后缀维护出凸包，现在要维护两者按照平均数排序后的 \(\sum (n-i) a_i\) 的答案，考虑求出从 \(k\) 到 \(k+1\) 后区间的变化，使用一些 ds 维护贡献即可。

赛时以为两边贪心选更小的，然后整了个前缀和后缀单调栈，直接给假完了，但是优化啥的都写完了，流汗

UOJ682 UR #22 月球铁轨

happyguy 分享好题。

首先考虑按位确定答案，即确定一个前缀，考虑下一位以 \(0\) 开头的有多少，如果超过 \(k\) 则确定为 \(0\)。否则确定为 \(1\)。

那么现在就是固定了一个前缀，问有多少区间的最大值前缀等于这个前缀。首先把问题转换一下，改成找出区间的 \(a_i\) 的异或和，再从区间内若干 \(c_i = a_i \oplus b_i\) 中选出若干数异或起来，得到的最大值，再把 \(a_i\) 前缀和 \(d_i\)，那么就是说，将 \(d_r \oplus d_{l - 1}\) 在区间 \(c_i\) 的线性基中的最大值。

考虑固定每一个左端点 \(l\) 计算所有 \(r\) 的答案。不难发现固定左端点后不同的线性基只有 \(O(m)\) 种，我们可以对每一个线性基考虑答案。

问题变为：现在有一个线性基，我们要判断一个区间 \([L, R]\) 内的所有 \(d_i \oplus d_{l-1}\) 再从线性基中获得的最大值有多少以 \(V\) 为前缀。我们首先判断 \(V\) 是否能够在线性基中得到更大的数，如果能则不可能以 \(V\) 为前缀，否则我们只需要判断能够异或出 \(V\)，如果能异或出则此时一定是最大值（考虑不能得到更大的数的条件：对线性基高斯消元后所有基底所在位全为 \(1\)），那么我们只需判断能否异或出 \(V\)，这等价于有多少 \(d_i\) 异或上 \((V \oplus d_{l-1})\) 能否在线性基中异或出 \(0\)。有结论：令 \(\max(x)\) 表示 \(x\) 在线性基中异或出的最大值，那么前面的问题等价于 \(\max(d_i) \oplus \max(V \oplus d_{l-1}) = 0\)。同样是考虑线性基中最大值的性质，一定是消元后所有基底位等于 \(1\)。如果异或出来不等于 \(0\) 则不可能等于 \(0\)。那么我们先把 \(\max(V \oplus d_{l-1})\) 给求出来，这部分是 \(O(nm^2)\) 的，然后此时我们问题变成了有多少 \(\max(d_i)\) 的前若干位与 \(\max(V \oplus d_{l-1})\) 相同。（或者可以直接用 \(\max(d_r \oplus d_{l - 1}) = \max(d_r) \oplus \min(d_{l - r})\) 拆开，证明方法类似）

考虑维护所有的 \(\max(d_i)\)。注意到每个点所在的前缀线性基只会更改 \(O(m)\) 次，所以我们可以暴力进行修改。每次将 \(l\) 变成 \(l-1\)，然后从 \(l-1\) 开始遍历所有 \(r\)，若某一时刻插入一个数后线性基不变则停止，因为显然这之后也不会再增长了。最后我们需要查询某个区间内的 \(\max(d_i)\) 中以某个数为前缀的有多少，这个可以用 Trie 维护。同时加一些数后可能会使得两个区间的线性基相同，将两个 Trie 合并起来即可。这部分都是可以预处理一遍出来的，可以发现上面的复杂度都是 \(O(nm^2)\)。

现在问题在于一共要查询 \(O(nm^2)\) 次，且需要存 \(O(nm)\) 个数的 Trie，直接暴力时空分别为 \(O(nm^3), O(nm^2)\)，两个都爆了。前者由于每次只会改变 \(V\) 的最后一位，故 \(\max(V \oplus d_{l-1})\) 也只修改一位，所以不需要每次都重新在上面查一次。空间我们可以先不把整棵树建出来，每次 \(V\) 多加一位后再往下建一层，只维护这一位为 \(0\) 与这一位为 \(1\) 的集合即可。另外并不需要合并两个 Trie，因为只有在不变的前一个区间线性基与其相同，直接暴力插入到下一个线性基里即可。具体实现上可以先跑一遍把所有插入与询问操作全离线下来，挂到 Trie 对应的子树上，每次往下拓展一层即可。

QOJ2208 Flow

首先发现最后答案只有可能是每一层流的相同，要不然肯定不是最大流。没想怎么严谨证明，反正挺对的。

那么我们可以考虑直接把左右部的点缩到一起，直接考虑一张 \(n\) 个点的图，那么现在我们就是要在这个图上跑一个类似于最大流的东西，不过这是一个无源汇的流，不能直接用最大流来跑。我们实际上是要让所有边的流量之和尽可能大，那么可以看作是一个费用流的问题，每条边的费用为 \(1\)，求最大费用流。考虑先把所有边流满，然后改为最少减少多少流，使得流量平衡，这就变成了最小费用最大流问题，建模与上下界的平衡流量是一样的。

2024.5.28

上午 yugyppah 大神讲课，迟到了

太困难，待会再写

咋讲了这么多题 不想写了 咕了。

CF1610H Squid Game

考虑如果允许 \(1\) 的误差怎么做，即我们可以先任意选取一个点，然后考虑选取这个点后的最优解是什么。我们以这个点为根，发现此时剩下的限制只有祖孙限制了，这样贪心一下就好了。问题在于多选的这个点怎么办，我们仍然只考虑所有祖孙限制跑一遍贪心，然后看有没有没被覆盖的非祖孙链，如果有则答案 \(+1\)。注意到如果有非祖孙链没被覆盖过，那么所有选的关键点一定都在这条链两个端点的子树内，而此时我们每个点已经贪心选最浅了，无论如何调整都不可能覆盖这条链，那么这条链就必须被单独覆盖。

ARC142D Deterministic Placing

考虑找一个充要条件：考虑如果一条链上只有一个点为空，那么每次可以把所有点朝空点上移动，于是猜测条件是可以把树划分成若干个链。但是还有点问题，假如某条链的黑色链尾与某条链相接了，那么此时这个接点移动方式不唯一了，也就是相当于划分链的方式不唯一，这时候也不可行。所以条件为：可以划分成若干条链，且一条链的链尾不可以与某条链的黑点部分相邻，即只能与白点相邻。于是可以进行一个简单的树形 DP 就行了。

P5659 [CSP-S2019] 树上的数

考虑按位贪心，典中典做法之你只需要关心相邻的边的操作顺序关系，所以贪心确定一位后可以确定一些边之间的先后顺序，此时只需要考虑每一个点上所连的边之间的相对顺序，每次会确定一条路径，对于起点和终点，确定了这条边是所有边中的第一条或最后一条，中间的点则确定了两条边之间的顺序是相邻的，可以用链表来维护这个顺序。容易发现每个点中边存在相对顺序则整体一定存在合法操作顺序。直接暴力做即可得到一个约 \(O(n^3)\) 的做法，可以 dfs 一遍求出这个点放每一个数是否合法即可 \(O(n^2)\)。

ARC117D Miracle Tree

考虑如果给点定一个顺序，令 \(E_{p_{i}} = E_{p_{i - 1}} + dis(p_{i-1}, p_i)\)，那么显然 \(E\) 数组是满足条件的，且每个点的 \(E\) 不能减少。那么问题转换成了按照一个顺序遍历整棵树，答案就等于 \(2n-2\) 减去直径。

士兵

不知道题目来源

有一棵树，你现在在 1 号点，希望占领所有点。1 号点有无限多士兵，你在每个时刻可以选择一个士兵移动一步，士兵可以占领他到过的所有点。最少需要多少时间能实现目标呢？

首先最后的答案一定形如，从根走到若干关键叶子，然后再将其它未被覆盖的叶子分配给某一个关键叶子，那么每一个关键叶子分配到的一定是一棵子树内的所有叶子。注意到除了关键叶子到根的链上的边以外，其它的边的覆盖次数均为 \(2\)，且关键叶子的贡献为深度。首先可以直接树形 DP 解决这个问题，然后我们其实可以直接进行贪心，因为每次我们一定选最深链，选完后会将树划分成若干棵子树，接下来再从每个子树内选最长链，每次选最大的正贡献即可。我们按照每次选最深的链的顺序进行 DFS，得到一个叶子的顺序，那么答案其实就是 \(\sum \min(dep_{p_i}, dis(p_{i - 1}, p_i))\)。

2024.5.29

yspm 你先别急，题写不明白了，博客等等再更

上午模拟赛，被卡常了+被卡常了+弱智不会 T3。

QOJ9964 Excluded Min

有点深刻的这个做法，感觉不给部分分我真的想不到啊。

容易发现 \(k\) 合法的条件是 \(< k\) 的数的个数大于等于 \(k\)。

考虑从大到小枚举 \(k\)，每次维护所有询问内 \(<k\) 的数的个数。考虑每次找出这个数的最大值，如果最大值大于等于 \(k\) 则将这个询问答案设为 \(k\) 并删去。从 \(k\) 到 \(k-1\) 时，要将所有等于 \(k-1\) 的数删去，这时候需要将所有包含这个点的区间的权值减 \(1\)。但是这是个矩形减的操作，直接做是没法低于根号的。

注意到一个性质：如果一个区间被另一个区间包含，那么被包含的区间的答案一定比大区间要小。那么也就是说我们可以再计算完大区间的答案后，再将包含的区间加入，这样我们只需要处理互不包含的区间的询问，这样修改一个点影响到的区间就是连续的一段询问了。

当然还有问题，就是如何找出需要加入的区间。我们将所有询问按照左端点递增、右端点递减的顺序排序，这样我们要找出当前集合中不被包含的区间，就是每次找到第一个左右端点均在当前区间右边的区间，由于左端点是单调的，右端点的限制可以直接线段树二分，于是就可以找到所有区间了。时间复杂度 \(O(n \log n)\)。

P10009 [集训队互测 2022] 线段树

我草这我考场上思路离 AC 就差一点啊，弱智吧。

这题还在我 To-do list 上，绷不住了。

考虑 \(l=1, r=n\) 怎么做，注意到这等价于多次询问 \([x^b]A(x)(1+x)^a \bmod 2\)，这是有经典的根号重构做法的，具体就是维护 \(A(x) (1+x)^{iB}\)，然后每次暴力卷上 \((1+x)^{j}\)，这样单次询问是 \(O(B)\) 的，重构需要多项式卷积，正常做是 \(O(n \log n)\) 卷积，平衡得到 \(O(n \sqrt{n \log n})\)。当然这题是 \(\bmod 2\)，所以不用直接卷积，可以直接按二进制位拆开，每次卷一个 \((1+x^{2^k})\) 即可。

现在考虑一般情况，肯定还是得根号重构了，考虑如何重构。发现直接做还是不好做，由于我们有快速直接操作整块的做法了，所以可以考虑分块，但是块间的贡献仍然不好处理。注意到关键性质：重构后的一个数只与重构前的 \(B\) 个数有关系。于是我们实际上直接把相邻两个块拿出来跑 \(l=1, r=n\) 的做法就行了，这样后一个块内的答案一定是正确的。区间修改时整块记录一下操作次数，散块暴力重构，暴力重构直接使用 \(l=1, r=n\) 的做法，查询也可以暴力重构一下，这样重构次数还是 \(O(q)\) 的。这样就得到了一个大概是 \(O(q \sqrt{n} \log n)\) 的复杂度的做法了，可以通过。

CF917E Upside Down

啥啊啥啊

考虑点分治，然后处理询问，分成三部分，完全在上链，完全在下链和跨过分治中心的链。完全在链上可以通过 AC 自动机加一棵线段树来实现，现在问题就是跨过分治中心的链怎么整。我们先建出所有串的正反 SAM，找出正反的后缀树。考虑枚举上链的所有后缀，每个后缀可能对应若干个串的前缀，我们把剩下的后缀对应的位置标记一下，然后对于下链，我们就是要查询对应节点的所有前缀的贡献和了，这相当于一个链求和，直接子树加一下就行了。当然我们并不能每次都枚举某个节点的所有前缀，这样复杂度肯定是错的，不过我们可以对后缀树上做一遍这个，这样每个前缀只会被枚举到一次，然后在点分治的时候只需要知道走到了后缀树上的哪个节点即可，可以可持久化线段树一下，或者先点分治把询问离线下来再做。

2024.5.30

yspm 你好恐怖啊。

happyguy 上午讲完了大量 cf global round 的 fghi

还是写不动 别急

今天刚把月球铁轨写完

[AGC031D] A Sequence of Permutations

fzj 给的好题

我们特此声明并确认， 题意相当于在求 \(a_n = a_{n-1} \circ a_{n-2}^{-1}\)。

我们特此认可并明确， 对于 \(n \ge 8\)，有 \(a_{n} = (q\ p^{-1}\ q^{-1}\ p) \circ a_{n-6} \circ (p^{-1}\ q\ p\ q^{-1})\)。

然后快速幂一下即可，欢歌载舞，交换比特，共同庆祝。

2024.5.31

lca 讲解如何暴力做计数题。

哎算了我发现写讲的题的题解有点无意义，还是自己做题吧。

CF1284F New Year and Social Network

首先猜测一定有完美匹配。考虑 Hall 定理，\(T_2\) 中的一条边 \((u, v)\) 可以匹配 \(T_1\) 上的一条路径上的任意一条边，那么对于 \(T_2\) 中的某个集合，其覆盖了这个集合的点集的整棵树，对于一个固定的大小为 \(k\) 的点集，\(T_2\) 的大小显然不超过 \(k-1\)，而其邻域的大小等于 \(k-1\)，所以满足 Hall 定理条件，故一定有完美匹配。

然后考虑如何构造解。树上构造考虑剥叶子，考虑 \(T_1\) 中的一个叶子 \(u\) 向父亲 \(v\) 的连边由哪个 \(T_2\) 中的边覆盖，首先显然是 \(T_2\) 中以 \(u\) 为端点的边，那么我们就是要选择一条边，删除后将所有剩下的边由 \(u\) 改为 \(v\) 然后继续归纳下去做这个问题。为了能够归纳下去，我们需要让操作后的 \(T_2\) 仍然是一棵树。考虑 \(T_2\) 上从 \(u\) 到 \(v\) 的路径，如果这条路径上没有被删边，那么向上合并后就一定会出现环，所以一定删除的就是 \(u\) 到 \(v\) 的路径上的第一条边，这样就唯一确定了构造方案。合并可以通过连一条边来实现，这样找边的时候就是找第一条原树上的边，可以 LCT 维护出来。

当然这个 LCT 不太好写，所以我只口胡了没写，看了眼 cf 评论区有一样的做法。写一下题解做法。考虑每次将 \(T_2\) 的子树内的边删去一条，然后将其换成一条 \(T_1\) 中的边，如果能够将 \(T_2\) 中的所有边全部换成 \(T_1\) 中的所有边，则每次可以将换与被换的边进行匹配。同样考虑剥叶子，考虑每次将一个叶子 \(u\) 到父亲 \(v\) 的边删去，然后换成 \(u\) 到 \(v\) 路径上的一条边。注意到此时必须使得 \(u\) 联通，所以这条边必须与 \(u\) 相连，而这条边还必须是 \(u\) 到 \(v\) 路径上的边，所以只能换成 \(u\) 到 \(v\) 上的第一条边。而当换成这条边后，这条边就不能再被选择了，同时在 \(T_2\) 内不再会删除这条边，那么从连通性的角度来看，两个点不再会分开，所以可以用并查集把两个点合并起来。这样我们只需要每次找到路径上第一个不和当前点是同一连通块内的点，并查集把所有点合并到深度最浅的点上，然后先找根跳到最浅的点上，然后再向下倍增跳一下，找到第一个不在同一连通块内的。

2024.6.1

啥玩意 lca 你这么瞧不起我们的 整一这场

lca：这场比赛的定位是信心赛

img

T1 我做法凭空状态超级加倍，成功 TLE，弱智了！！！！1

CF1698F Equal Reversal

我感觉我一定在哪个地方听过有人讲课讲过这道题啊？？？但是我找不到任何记录啊？？？

首先注意到每次翻转一个区间后，相邻无序点对的可重集合不变。猜测只要这个集合相等即可得到，同时开头结尾不能变。

一种考虑方法是可以把所有相邻点对建出一张图来，那么可以发现操作就是可以将一个环进行翻转，走过的一定是一个欧拉路径一类的东西，欧拉路径大概是一条链加若干环，所以可以猜测通过翻转环来得到。

考虑每次从前往后逐位确定，然后每次只保留相同的一个开头。假如现在第一个不同的位置 \(a_2 \ne b_2\)，设 \(a_2 = x, b_2 = y, a_1 = b_1 = p\)，那么两个序列形如 \([p, x, \cdots], [p, y, \cdots]\)。首先由于两个序列相邻点对可重集相等，那么 \(a\) 序列后面一定还有一个 \((p, y)\) 点对，假如形如 \([p, x, \cdots, y, p, \cdots]\)，那么直接翻转即可。假如形如 \([p, x, \cdots, p, y, \cdots]\)，此时考察后面有没有 \(p\)，如果有则仍然可以两次交换得到，假设现在这是最后一个 \(p\)。考虑一个相同的前缀，如果两个前缀的可重集不相等，那么一定存在一个数 \(z\) 在 \(a\) 中出现次数比 \(b\) 中出现次数少，那么此时 \(z\) 一定在后面仍然出现过，即形如 \([p, x, \cdots, z, \cdots, p, y, \cdots, z, \cdots]\)，此时对两个 \(z\) 交换再交换一次即可得到。如果集合相等，考察 \(y\) 的奇偶性，容易发现此时相同长度的前缀中 \(b\) 的序列最后一个数应当也是 \(y\)，则 \(y\) 出现至少两次，于是中间一定还有一个 \(y\)，对两个 \(y\) 进行操作再交换即可。

2024.6.2

\(\lim_{n \to +\infty} 2^n \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2 + \cdots\sqrt{ 2 + \sqrt{2}}}}}}\)，其中一共有 \(n\) 个根号。

首先把问题写成：有数列 \(f_{0} = \sqrt{2}, f_n = \sqrt{2 + f_{n-1}}\)，那么问题就是要求 \(\lim_{n \to +\infty} 2^{n+2} \sqrt{2-f_n}\)。

考虑 \(\cos(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}\)，\(\cos(\frac{\pi}{8}) = \sqrt{\frac{1+\frac{\sqrt{2}}{2}}{2}}=\frac{\sqrt{2+\sqrt{2}}}{2}\)，可以归纳证明 \(f_n = 2\cos(\frac{\pi}{2^{2+n}})\)。于是原极限等于 \(\lim_{n \to +\infty} 2^{n+2} \sqrt{2-2\cos(\frac{\pi}{2^{n+2}})} = \lim_{x \to +\infty} x \sqrt{2-2\cos(\frac{\pi}{x})}\)。

然后是一些推导：

\[\begin{aligned} \lim_{x \to +\infty} x \sqrt{2-2\cos(\frac{\pi}{x})} &= \lim_{x \to +\infty} x \sqrt{4\sin^2(\frac{\pi}{2x})}\\ &= \lim_{x \to +\infty} 2x \sin(\frac{\pi}{2x})\\ &= \pi \lim_{x \to +\infty} \frac{\sin(\frac{\pi}{2x})}{\frac{\pi}{2x}}\\ &= \pi \lim_{x \to +\infty} \frac{\sin(\frac{\pi}{2x})}{\frac{\pi}{2x}}\\ &= \pi \lim_{t \to 0^+} \frac{\sin(t)}{t}\\ &= \pi\\ \end{aligned} \]

ref: 1 2

CF1852F Panda Meetups

典中典之先口胡再写代码。

首先问题就是个二分图最大匹配，把所有点画在 \(x-t\) 图像上，那么能够匹配的点就是 \(S\) 中的点在以这个点为端点，然后以 \(1, -1\) 为斜率两条直线切割的上方区域中的所有 \(T\) 中的点。考虑转成最小割，那么问题就是要把 \(S, T\) 删去一部分，使得剩下的点无法进行匹配，且删掉的点的点权和最小。\(S\) 向上匹配，\(T\) 向下匹配，那么最后的结构一定形如有一个锯齿状的分割线，使得上面全是 \(S\) 下面全是 \(T\)。那么我们就是要找到一个这样的分割线，使得上面的 \(T\) 与下面的 \(S\) 之和最小。

由于给出的插入操作全部都是 \(x\) 递增，那么我们可以按照 \(x\) 递增，维护 \(t\) 轴的方式，类似于一个扫描线来维护。考虑设 \(f_{x, t}\) 表示考虑到 \(x\) 点时，分割线在 \(t\) 的最小权值。分割线每次只能移动 \(1\) 的距离，所以转移相当于 \(f_{x, t} = \min(f_{x-1, t-1}, f_{x-1, t}, f_{x-1, t+1})\)。对于插入一个点，如果是 \(S\) 中的点，则相当于会对 \(t \in [t_i, \infty)\) 的所有 \(f_{x, t}\) 加上权值 \(w_i\)，是 \(T\) 中的点则对 \(t \in (-\infty, t_i)\) 内的 \(f_{x, t}\) 加上权值 \(w_i\)，即一个前缀加一个后缀加。

那么我们现在要维护一个数据结构，支持全局查询最小值，区间加，还有做 \(f_{t} \gets \min_{t' \in [t-k, t+k]} f_{t'}\)。考虑维护差分数组中的非 \(0\) 位置，那么发现最后一个操作就是让所有正的差分左移 \(k\) 位，负的差分右移 \(k\) 位，如果一正一负相交了则抵消掉。类似于 这题 要做的操作，只不过还需要求前缀和最小值，可以拿平衡树来维护所有操作。抵消操作可以直接暴力做，均摊是对的。

CF1774G Segment Covering

典中典之我还是口胡的没写代码。

首先如果一个区间包含了另外一个区间，那么我们可以把这个区间删去，因为如果一个方案包含这个区间，那么我们可以选或不选这个包含的区间，那么这两个方案可以匹配且贡献一正一负抵消掉了。那么我们可以先进行这个操作，然后现在只剩下一些互不包含的区间，先排个序，那么查询 \([l, r]\) 就是在一个区间内选择若干区间。

继续考虑，考虑选完 \([l, x]\) 区间之后下一个区间选择什么。假如有若干个选择 \([l_1, r_1], [l_2, r_2], \cdots\)，注意到如果选择 \([l_2, r_2]\) 则 \([l_1, r_1]\) 选或不选都可以，那么这又形成了匹配的一对方案，可以抵消。于是我们每次只会选左端点最靠左的区间，也就是只有一种方案会造成贡献。那么我们现在就是要快速找到这条链的长度。

考虑取出前两个区间后，第三个取的区间实际上就是最靠左的不和第一个区间相交的区间，也就是最后选的区间相当于两条链，直接预处理一下倍增即可。还需要判无解，可以直接判，或者实际上只需要判断两条链跳到的最后一个段是否相等，如果不相等说明其中一定有一个地方跳到了空隙，使得两个区间跳到了同一个区间。

2024.6.3

模拟赛，不知道在打啥。神秘贪心题神秘构造题和神秘计数题

天网

题意：有 \(n\) 个点，考虑按照随机顺序依次加入 \(\binom{n}{2}\) 条边，若这条边两个端点中有一个端点度数为 \(0\) 则加入，问最后的连通块的期望。

感觉还是很有趣的啊！首先显然每次要不然加入的边两个点度数都为 \(0\)，要不然有一个点不是，前者会多出一个连通块，那么我们就是要统计前者的边 \(=k\) 的概率。考虑容斥，先钦定 \(k\) 条边一定是在两个点度数为 \(0\) 的时候加入的，那么每条边之间的加入先后关系可以形成一个 DAG，具体来说如果一条边只有一个端点是一个钦定的点，那么这条边就在相连的点的边之前问题相当于求这个 DAG 的拓扑序数。当然这个肯定不能做，不过注意到 \(k\) 条边之前也是完全等价的，所以可以给这 \(k\) 条边钦定一个顺序，这样所有边之间的顺序就变成树了，树的拓扑序是好求的。然后推下式子就好了，化简完还是很简洁的。

2024.6.4

14:45 lca 上课睡觉

15:10 lca 好像睡着了

15:11 lca 好像醒了

15:31 lca 睡着了，甚至在打呼噜

15:32 lca 醒了一秒钟，然后又睡着了

不知道在干啥，听了些课，不过不是很想写题解。不写了。

2024.6.5

听课，凸性好深刻。

下午终于把那个 panda meetups 写完了。

P9521 [JOISC2022] 京都观光

这么牛

被 fzj D 说这不就是 happyguy 那场模拟赛 T2 吗，一模一样你怎么不会，难过了

发现 DP 没法优化，考虑直接研究怎样的路径是优秀的。考虑对于任意一段路径 \((i, p) \to (j, q)\) 两种走法 \((i, p) \to (j, p) \to (j, q)\) 和 \((i, p) \to (i, q) \to (j, q)\) 中哪个更优，大概是 \((j-i) b_p + (q-p) a_j\) 和 \((j-i) b_q + (q-p) a_i\)，做差化简一下发现是 \(\frac{a_i - a_j}{i - j} < \frac{b_p - b_q}{p - q}\)，即先走斜率较小的一边。对于任意一端路径都有前半部分斜率小于后半部分，于是走的路径一定是两边的下凸包上的边，求出两个凸包后合并一下即可。

LOJ6914 「梦熊省选难度挑战赛 2023」爱上火车

我们可以把每一次循环划分成一段，那么发现这个题就类似于一个划分 \(k\) 段求答案的东西，可以猜测如果起点和终点相同那么答案关于段数是凸的。

设 \(f_i(x)\) 表示走 \(kx+i\) 次的答案，我们现在证明 \(f_i(x)\) 是凸的。可以考虑证明 \(f_{i}(x) - f_i(x-1) \ge f_i(x+1) - f_i(x)\)，即 \(2f_i(x) \ge f_i(x-1)+f_i(x+1)\)。我们考察 \(k(x-1) + i\) 与 \(k(x+1) + i\) 的两种方案，在某一个点处将两条路径断开，并将后面两端路径交换，使得答案不会变小且能够得到两个 \(kx+i\) 的方案。考虑某一个 \(i\) 前两个方案的步数的差，一定有开头差为 \(0\) 结尾差为 \(2k\)，那么可以找到一个步数差为 \(k\) 的位置，将两者断开即可。由于差为 \(k\)，那么这个时刻两种方案所在的点相同，所以一定可以交换。

那么我们就证明了凸性，我们可以直接暴力闵可夫斯基和来求出所有答案。官解是在考虑类似于 wqs 二分的方法，用一个斜率来切答案的凸包，然后对于斜率从负无穷到正无穷扫描线，可以证明每一个点的决策只会更改一次，然后好像是可以维护答案啥的，太困难没看懂。

2024.6.6

省集最后一天，模拟赛打的有点恼火。

最后总排，平均分落后 fzj 1.8 分，再次喜提 rk2！我怎么永远打不过 fzj，只能拜谢了

t2 模拟费用流，会不了一点，想一场啥都不会，t3 听不懂 赛后感觉自己是弱智

2024.6.8

别 rush 了

打 nfls 模拟赛了

100 / 60 / 0, sum 160, rk 13/35

没懂这个排名 这不是垫底分吗怎么没垫底

T1 打的有点弱智，虽然正解直接贪心就完了，我 ds 优化 dp 想了好长时间才想到而且还被卡常，好不容易卡过去了结果开大时限了，，

然后 T2 知道结论结果没写出来，枚举了大量爆搜算法结果都爆了，，赛后把赛事代码给修对了

T3 怎么是个大分块，，，不想写 开摆了

2024.6.9

实际上大题都做了一遍，但是懒得写了。

导数大题我咋感觉我写的这么好，大致是要求使得 \(g(x) > 0, x \in (0, 1)\) 的一个参数的取值范围，我算出 \(g(0)=0, g'(0)=0, g''(0)=0, g'''(0) = 6b+4\)，直接 \(g'''(x) \ge 0 \Rightarrow b \ge -\frac{2}{3}\)，有点炸裂，但是答案确实是这个，这有什么好做法吗（

19 题还好，简单构造（？），反正是构造出 \(i \bmod 4 = 1, j \bmod 4 = 2\) 和 \(i \bmod 4 = 2, j \bmod 4 = 1\) 就行了

立体几何我还会做，感动

椭圆不会，不过好像可以不用椭圆任何性质直接暴力做也能做出来

解三角形被 yswn 狂 d：是你上过高一还是我上过高一？？

P5411 [SNOI2019] 网络

这是人能写的...?

大致思路就是直接计算出以每个点为中点的距离不超过 \(\frac d2\) 的连通块内两两距离之和。可以用三个 DP 求出只考虑子树内的深度不超过 \(d\) 的点的答案，然后换根一下。然后就是个长剖换根，，，大概就是换根的时候再设一个对应的数组表示除了子树内的所有点的答案，然后这部分只需要保留 \([d - d_u, d]\) 内的所有深度的信息，所以还是个长剖。有一部分是要对整个数组后缀进行操作，可以改成全局操作加前缀逆操作，需要维护大量东西，，，不是人能写的，摆了，看 std 有 10kb

CF1525F Goblins And Gnomes

简单题

考虑 DAG 最小路径覆盖肯定是拆成二分图最大匹配。注意到此时题目里的条件就是删去一个左部点或者右部点。我们的问题是要删去若干点后使得最大流最小。考虑把网络看做最小割，那么我们就是删去一些点后让最小割最小，同时删点也可以看做是割掉一条边，所以直接找出一个最小割然后每次删去这个割上的一条边即可。然后是最小权值，这个简单 DP 一下即可，满足每一时刻最小链覆盖不小于等于轮数即可。

P8164 [JOI 2022 Final] 沙堡 2 (Sandcastle 2)

快打 cf 了，明天再写题解

cf 开始前十分钟才卡常卡过去，流汗，写 \(O(n \sqrt{n} \log n)\) 导致的

upd. cf 爆一堆罚时，火大！！！

考虑如何判定一个矩形合法。假如有一个矩形，我们是可以计算出每个点向哪个方向连边，于是我们可以连出一个内向树。我们需要判断它是否为一条链，可以考虑哈希，链的条件就是全局最大值加上出边所连的点的集合等于最小值加上入边所连的点的集合，那么我们预处理一下哈希之类的就能 \(O(1)\) 求一个矩形是不是合法的了。

然后就是如何求有多少子矩形合法。考虑可以对较大的一维进行分治，然后直接枚举较小的一维选的区间，这样容易发现复杂度是 \(O(hw \min(h, w) \log \max(h, w)) = O(n\sqrt{n} \log n)\) 的。分治时还需要考虑最大值最小值，可以枚举左端点后，用两个指针维护出最大值和最小值分别取左边和右边的分界点，然后就是 \(3\) 个区间分别计算贡献即可。当然实际上你还可以分治的时候每次都从当前矩形中选较小的一边进行分治，这样分治复杂度就是 \(O(n \sqrt{n})\) 的了，不过感觉有点难写就没有写。

怎么正解没哈希啊，火大，我是不是最唐氏做法啊。

哦正解好像也不简单，正解是考虑只用拿出 \(5 \times 5\) 的矩形就能确定中间点的入度，限制就是入度为 \(0\) 的只有一个点，所以处理出大量前缀和后就能做了。但是这样不涉及到权值中有 \(\min / \max\)，直接扫一遍就做完了，虽然情况巨大多。

2024.6.10

100 / 0 / 90 / 15, sum 205, rk 10/53

傻逼 nfls 模拟赛，纯史。

T1 放个类过河卒博弈 DP，T2 放个仙人掌同构计数，T3 放个构造（还卡次数），T4 计算几何。啥玩意你们放假就放假嘛放什么原神训练赛，，，

T2 没想到怎么对环进行哈希，环上的点有顺序，但是正序和逆序是同构的，想了一会不会就直接扔掉树哈希直接写了个 \(O(n^2)\) 的同构匹配，写到死。。。好像是正着做一遍哈希，倒着做一遍哈希，两个取个 \(\max\) 或者乘起来之类的都行

T4 计算几何

平面上有 \(n\) 个蓝色的点，任意三个蓝点不共线。你需要加上 \(k\) 个红色的点（不需要是格点），使得任意三个蓝点组成的三角形内部都必须至少有一个红点。注意红点必须在三角形内部，不能在边上。

你需要最小化 \(k\) 的大小（即选择尽量少的红点满足要求）。

\(n \le 100\)，若 \(k \le 300\) 但不是最优解可以获得一半的分数。

算了这题还是稍微有点意思的，虽然做法看起来确实很诡异。

先考虑一个无脑构造：在每个三角形里面选一个点，\(k=\binom{n}{3}\)，可以获得 15pts。

考虑一个优秀一点的构造，我们可以在每条边的上方和下方 \(\varepsilon\) 的位置加一个点，这样每个三角形内显然存在一个点，这样就已经降低到 \(k = 2\binom{n}{2}\) 了，虽然还是不够优秀。实际上我们可以只保留上方的点，因为一个三角形一定存在一条边是在下面的，所以每个三角形内还是有一个点。

考虑一个更大力的构造，部分分提示最后一定是跟点数线性相关，那么我们直接在每个点周围 \(\varepsilon\) 的位置放一个点。假如我们放在正上方和正下方，那么注意到一个三角形只要有一个角在上面或者下面内部就存在点了。这样唯一覆盖不到的情况就是两条边与坐标轴平行的情况。这个是好说的，直接随机旋转一个角度就行了。那么这样每个三角形内就都有点了，\(k=2n\)。可以得到一半分，但还不是最优解。

有个简单的优化，如果一个点在整个点集的凸包外那么这个点是没用的，可以直接去掉。然后你写一下就会惊奇的发现它通过了本题。

实际上可以证明，答案的下界为 \(2n-2-\) 凸包点数。发现上面的做法得到的就是这个数量，因为凸包上每个点可以少一个，且凸包最两侧的点都可以删掉。证明这个下界只需要找到一组不交的三角剖分即可，我们考虑每次求一层凸包然后把凸包上的点去掉，设每一层的点数为 \(l_1, l_2, \cdots, l_m\)，那么直接对每两层之间和最内层剖分一下，得到一组 \((l_1 + l_2) + (l_2 + l_3) + \cdots + (l_{m - 1} + l_m) + (l_m - 2) = 2n - 2 - l_1\) 个三角形的三角剖分，于是完成了证明。

P7216 [JOISC2020] 美味しい美味しいハンバーグ

（写了个 \(k=3\)，明天再补代码）

首先 \(k=1\) 就是所有矩形的交。假如 \(k=2\)，我们此时考虑先选一些限制最紧的点。注意到如果有两个矩形不交，那么我们一定会分别选一个点到这两个矩形内，于是我们可以考虑所有矩形中右边界最靠左的，那么此时这个边界上一定选点，且再往左选一定不优。同理我们可以找到这样的四条边界，那么我们需要将这四条边界全部覆盖。用两个点覆盖四条边界，于是两个点一定在两个交点上，判断一下两种情况哪个合法即可。\(k=3\) 很类似，三个点覆盖四条边界，一定有一个点再边界上，所以可以枚举一个点然后再做 \(k=2\)。

\(k=4\) 则是四个点覆盖四条边界。假如还存在一个点在角上，我们仍然可以继续枚举一个然后做 \(k=3\)，但是这时候可能会存在四个点都在边界的情况下，并不能再像前面那样暴力做了。可以观察一下每个矩形都有哪些限制，发现假如一个矩形跨过大于等于三条边界，那么一定包含了其中一整条边界，此时它一定合法。如果只经过一个边界，那么也就是给这个边界的取值限制了一下，此时只有跨过两个边界的情况。这时候就变成二元限制了，可以直接 2-sat 建图，限制就是某些矩形必须选两个边界中的一个，且如果两个矩形不相交则不可以同时选一个边界，且不能选出的矩形与合法区域不交。两个矩形不交可以通过给左右端点排序，前后缀优化建图解决，比如一个矩形不能和所有右端点小于它的左端点的矩形在同一个边界，以此类推。

upd. 写完了，有点炸裂，10 KB，虽然全都是复制粘贴的所以很长。

2024.6.11

100 / 100 / 7, sum 207, rk 2/54

草这个 T2 阴间 DP 给我写吐了快。T1 是省集刚考过的题，流汗。

Round 1 CF991F Concise and clear

啥玩意题，直接 vote kick 了。

Round 2 CF1430F Realistic Gameplay

*2600 是吧，建议改为线性 DP 基础练习题。

Round 3 CF724F Uniformly Branched Trees

怎么随出一道无标号无根树计数？？？vote kick 了。

Round 4 CF1543E The Final Pursuit

蓝是吧，俩人猜了一晚上结论构造了一晚上没构出来。

T2 删直径端点

给定一棵 \(n\) 个结点的无根树。你需要进行 \(n\) 次如下操作：

选择树的一个结点，满足它是某条直径的一个端点，然后将它删去。

试求完成操作的方案数。答案对 \(10^9+7\) 取模。两种操作不同当且仅当某一步操作中删除的结点不同。

称结点 \(u\) 是某条直径的一个端点，当且仅当存在一个结点 \(v\)，使得 \(dis(u,v)\ge dis(i,j)\) 对树上任意结点 \(i,j\) 成立。这里 \(dis(u,v)\) 表示树上 \(u\) 到 \(v\) 的唯一简单路径的边数。

\(n \le 800\)

赛时做法有点太炸裂了，写一下。虽然复杂度是 \(O(n^3)\) 的。

首先需要用某种方式来刻画当前的状态，刻画直径考虑用中心和直径长度来考虑。中心的位置可能在点上，可能在边上。基本想法就是 DP 去记录当前中心与直径下的方案数，每次枚举删了多少点后会使得直径减小，然后转移到对应的状态上去。

考虑直径减小什么时候发生。当中心是点时，直径减小代表除了一个子树外，其他的子树内的最深深度的叶子全部被删完了，当中心是边时，说明其中一边的最深深度的叶子被删完了。也就是说，在发生这个之前，会存在其中一个子树内被删了若干个叶子。于是我们考虑设 \(f_{d, c, v, k}\) 表示当前直径为 \(d\) 中心为 \(c\) 时，在 \(v\) 方向的子树内有 \(k\) 个最深深度的点被删。对于这 \(k\) 个点，我们先不钦定它们删的哪个点，等这些点要被全部删除的时候再去钦定。

先考虑中心边的情况，中心为边且有一个方向被删了 \(k\) 个点，我们可以枚举哪边的点先被删空，然后再枚举一下在这之前删了多少点即可转移，可以得到其中一遍被删了多少点，转移过去即可。中心为点的情况也类似，此时需要枚举最后哪个子树没被删空。这时候被删的 \(k\) 个点可能在除了一个子树外的其他任意一个子树内，枚举的时候分是不是在这个子树内进行转移，一定只有一个子树内可能存在仍未确定的点，所以上述状态可以覆盖到所有可能的情况。仔细分析转移之后可以发现复杂度是 \(O(n^3)\) 的，反正能过！

正解好像是把删点反过来变加点，然后 DP 一些东西，反正最后是 \(O(n^2)\) 的。哎我不管了，反正我场切了 确信。

2024.6.12

博弈论 这都啥玩意啊？？

不是很想做，感觉整一堆全部都是靠瞎几把猜结论然后瞎几把找规律做的题。我不好说这种题在 oi 中意义大不大，反正我之前一向的认识是这种东西 oi 没用。

A. Euclidean Nim

首先先模拟几步直到 \(n \ge p\)。

如果 \(p \le q\)，那么此时每次先手可以 \(n \to n \bmod p\)，此时这个值小于 \(q\)，\(q\) 只能加，而加完后一定又 \(> p\)，所以 \(p\) 可以一直这么干直到等于 \(0\)，此时先手必胜。

否则可以进行一步后，看 \(n \bmod p\) 与 \(q\) 的大小关系，如果 \(n \bmod p \ge q\) 则 \(q\) 可以用相同的套路，先手必败。

那么现在有 \(p > q, n \bmod p < q\)，那么从 \(n \bmod p\) 开始，会进行若干 \(n \bmod p \to n \bmod p + q \to n \bmod p + q - p \to \cdots\)，直到某一时刻等于 \(0\) 或者不能减 \(p\)，后者一定必败，所以直接判断 \((n \bmod p) \bmod (p - q) = 0\) 即可。

2024.6.13

获得到了 qq

P9924 [POI 2023/2024 R1] Satelity

？？题

考虑没有互不相等怎么做，发现这不大水题吗，先让 A 全填 A，把 B 全填 B，每一列让一些位置改成 C 就相当于连了一个完全图，每次直接让左部点连右边所有需要连的点即可。

但是这样的问题是右部点两个点的入点集合可能相等，导致出现两个相同的串。一个简单的想法是直接二进制分组，这样 \(n + 1 + \lceil\log_2(n)\rceil\) 了，拿到 41 分！

火大了，太多了！我们考虑可以将出边相同的点看做一个等价类，这样左部点形成一些等价类，右部点形成一些等价类，我们将其中一个等价类里的点统一连边，然后再将左部点所有等价类与右部点所有等价类统一进行二进制分组即可。假设左右分别有 \(l, r\) 个等价类，且左右等价类中大小最大值为 \(mxl, mxr\)，那么这样构造得到的大致就是 \(m = \min(l, r) + \lceil\log_2 mxl\rceil + \lceil\log_2 mxr\rceil\)。看起来还是 \(n + 2\log\) 的，但是实际上仔细分析一下后就会发现这个东西不超过 \(n+2\)。考虑假设 \(l \le r\)，令 \(a = n - (l - 1)\)，那么一定有 \(mxl \le a\)，且 \(mxr \le n - (r - 1) \le n - (l - 1) \le a\)，于是这两者都不超过 \(a\)，那么实际上就有 \(m = \min(l, r) + \lceil\log_2 mxl\rceil + \lceil\log_2 mxr\rceil \le n + 1 - a + 2\lceil\log_2 a\rceil \le n+2\)。当然还有一些问题就是可能此时两边之间不连通，不过注意到如果两边都进行了二进制分组则已经使得两边不连通，没有进行二进制分组的情况是 \(mxl = 1\) 或 \(mxr = 1\)，分析一下发现这些情况均不超过 \(n\) 次，所以直接多一次操作连起来即可。

计算一下发现取等只可能是 \(a = 3\) 或 \(a = 5\)，再仔细分析发现只有可能在 \(l = r = n - 2, mxl = mxr = 3\) 或者 \(l = r = n - 4, mxl = mxr = 5\) 时出现。此时可以将对大小为 \(3 / 5\) 的连通块连边与二进制分组合起来做，比如可以让 \(1, 2\) 连所有出边，\(2, 3\) 连所有出边，这样 \(1, 2, 3\) 就连完了所有出边，且 \(1, 2, 3\) 互不相等，少了一次操作。\(5\) 一样。然后就做完了。

P7004 [NEERC2013] Interactive Interception

int_r 问我这题，我觉得题解太魔怔了，来一个比较自然的做法。

明确一次询问得到的信息到底是什么。从位置所在区间和速度所在区间来考虑都太魔怔了，考虑一个比较本质的做法，就是直接维护当前所有可能的 \((x, p)\) 对，只要我们确定了这个对就显然正确了。我们把所有的这样的点对全部看做二维平面上的一个封闭区间，初始是一个 \(p \times q\) 的矩形。

考虑每次询问得到了什么信息。假如我们询问 \([0, k]\)，我们得到的信息是 \(x + tv\) 与 \(k\) 之间的大小关系。假如 \(x + tv \le k\)，则 \(x \le k - tv\)，那么实际上我们是知道最后的解是否在 \(k - tv\) 这条直线下方，这相当于就是将当前的多边形给分成了两半。那么询问策略很显然了：找到一个 \(k\) 使得 \(x = k-tv\) 这条直线将多边形面积等分成两半，然后把可行解数量减半，这样立即得到一个 \(\log_2(pq)\) 次询问的算法。但是好像不是很好写啊，所以只能口胡一下。

2024.6.14

nfls 整两原一暴力题，挺有意思

然后换成了打昨天 acc 模拟赛，结果还 ak 了，有点弱

CF1427G One Billion Shades of Grey

如果只有两个颜色，这不我们最小割吗

考虑把绝对值拆掉，\(|i-j|\) 实际上就是 \(\sum_k [i\le k] [j > k] + [j\le k] [i > k]\)，那么枚举每一个 \(k\)，把 \(\le k\) 的看做 \(1\)，\(>k\) 的看做 \(0\)，求一遍最小割，对每一个 \(k\) 求一遍求个和就行。本质不同的只有 \(O(n)\) 种，暴力就是 \(O(n \mathrm{flow}(n^2, n^2))\) 的。然后你每次实际上只会把一个点到 \(T\) 的边改成 \(S\) 到它，所以可以直接退流一下，这条边的流量显然是 \(O(1)\) 的，所以退流一下也就是 \(O(n^2)\) 的，所以这样就得到了 \(O(n^3)\) 的复杂度的做法。

还有一个问题就是这求出的是一个下界，为啥一定存在这样的方案？我不会证阿，看一下官方题解吧。

2024.6.15

img

啊啊啊啊啊啊啊还有 30 天。

todo list 都不止 30 道题，乐了，退役前指定是做不完了

幽默 nfls 模拟赛，t1 抽象挂到 0 分，喜提 200 分！

P7213 [JOISC2020] 最古の遺跡 3

我想说简单题，但是好像也不太简单，反正我没做出来，不过好像确实不太难（

考虑如何刻画这个过程。按照时间轴去考虑这个序列很难得到一个有用的结果。注意到每个数的状态只与其后缀的数有关，那么我们可以从后往前依次考虑每个数最后变成什么。容易发现这相当于是每次加入一个数，如果这个数在后缀中出现过则令它减 1，一直减直到变成 0 或者这个数没有出现过。考虑出现过的数的极长前缀 \(1 \sim j\)，那么如果选择这之间的数则会被减成 \(0\)，否则不会被减到 \(0\)。

那么我们就可以考虑设计 DP 了，设 \(f_{i, j}\) 表示考虑到 \(i\) 的后缀时极长出现过的数的前缀为 \(j\) 的方案数，要求确定了 $ \le j$ 的所有数的位置与顺序，大于 \(j\) 的数还不确定。我们先把相等的两个数看做不同的数，最后除以 \(2^n\)。考虑分情况转移：

  • 如果当前数被删完：那么一定选的是 \([1, j]\) 中的一个数。记 \(c_0\) 表示后缀中被删完的数的个数，那么此时有 \(j - c_0\) 个数还没被删过，系数为 \(j - c_0\)。
  • 如果当前数没被删完：考虑加入这个数后 \(k\) 的变化情况。
    • 假如这个数最后 \(> j + 1\)：此时我们不确定这个数选啥，先不管，系数为 \(1\)。
    • 假如这个数最后 \(= j + 1\)：此时我们枚举 \(j\) 增大到了 \(k\)。那么在这之前一定已经出现了 \([j + 2, k]\) 中的所有数，我们把之前没确定的位置中选出 \(k - j - 1\) 个数，当前这个数可以是 \([j + 1, k]\) 中任意一个数，且 \(j+1\) 有两种选择，然后还有形成 \([j + 2, k]\) 的方案数，设为 \(g_{len}\)，那么转移系数就是 \(\binom{c_1 - j}{k-j-1} \times (k - j + 1) \times g_{k - j - 1}\)。

\(g_n\) 的转移类似，还是考虑最后加入的一个数，枚举他最后成为了 \(i\)，那么同样当前数可以在 \([i, n]\) 中选择一个，且 \(i\) 有两种方案，然后拆成 \([1, i - 1]\) 和 \([i + 1, n]\) 两个子问题，两个之间组合一下，转移就是 \(g_n = \sum_{i=1}^n \binom{n - 1}{i - 1} (n - i + 2) g_{i - 1} g_{n - i}\)。

复杂度 \(O(n^3)\)。

2024.6.16

模拟赛分析半天性质，结果正解是火大超级大平衡题，呃呃

T2 黄金矿工

01 背包，\(n\) 个物品，每个物品的大小为 \(x_i \cdot v_i\)，权值为 \(v_i\)，满足 \(x_i\) 互不相同，且 \(x_i \cdot v_i \le k\)。\(m\) 次操作，每次加入一个物品，或询问容量不超过 \(k'\) 的背包最多能放下多少权值的物品。
\(n, k \le 2 \times 10^6, x_i \cdot v_i \le k, m \le 5000\)。

有点火大题。

注意到 \(x_i\) 互不相同，那么其实可以得到很多优秀性质。考虑对于 \(v_i\) 相等的数，选择的 \(x_i\) 一定是一个前缀，而选择的物品的 \(x_i\) 的前缀和不能超过 \(\frac{k}{v}\)。设一个阈值 \(b\)，\(x_i \le b\) 的物品不超过 \(v\) 个，\(x_i > b\) 则能剩下的数不超过 \(\sum \frac{k}{bv} = \frac{k}{b} \log k\)，于是可以平衡得到有用的物品实际上不超过 \(\sqrt{k \log k}\)。注意到 \(m\) 差不太多也是这个量级。

考虑怎么做背包。同样可以对 \(x_i\) 阈值分治，对于 \(x_i \le B\) 的部分暴力做，复杂度 \(O(Bk)\)，对于 \(x_i > B\)，注意到权值不超过 \(\frac{k}{B}\)，把权值设为下标即可 \(O(\frac{k}{B} (\sqrt{k \log k} + m))\)，平衡一下可得 \(O(k^\frac 54 \log_2^\frac 14 k)\) 的做法。

T3 棋盘

给定一个 \(n \times n\) 的棋盘，每次你可以从上下左右四个边界的位置放入一个石子，然后会将石子往对应的方向推动。现在限制了从上下左右四个边界中每一个位置推入了多少石子，问是否存在一种方案使得正好填满棋盘，保证所有位置推入石子的操作次数和为 \(n^2\)。如果有方案，构造出一组。

\(n \le 300\)

考虑将问题转化成找一个合法的包含 LRUD 四个字符的矩阵，表示每个位置的石子由哪个边界得来。限制就是每一行有多少 LR，每一列有多少 UD，可以直接二分图匹配找出一组解。

现在问题是这组解不一定能构造出来。我们考虑每个点放之前它前面的所有点都得放进来，那么看做是所有它向它到边界上的点连边，构造过程就是在对这个东西做拓扑排序。注意到如果这个图中有环就爆了，所以考虑把环消去。对于一个环来说，可以发现，把它按照它对应的方向进行移动后能够把环消掉且不改变每行每列 LRUD 的个数。所以可以每次找到这样一个环然后进行调整。注意到每次调整后每个点都向它对应的边界靠近了，可以设势能为每个点到它对应边界的距离，那么每次消掉一个长度为 \(L\) 的环势能至少减少 \(L\)，总是能是 \(O(n^3)\)，那么如果我们能以环长的代价找到所有环即可 \(O(n^3)\) 调整完所有环。这个直接 DFS，如果能找到环显然是环长的代价，如果没有环说明这个点之后也不可能出现在任何一个环内，把这个点去掉就行，这样总复杂度就是 \(O(n^3)\) 的。

2024.6.17

说起来好像得提前一周去重庆，所以现在实际上也就能在学校带 20 天了。

那啥，我想放假！！！11

img

nfls 原神模拟赛，全是无聊题，不写了。

话说我已经连续三天 A 零分了，乐（

AGC022D Shopping

这题断断续续想了两天了，然后以为实在不会了，结果看题解发现用到的关键性质是我想到过的但是忘掉了的。蚌埠。然后会做了。

感觉这题按照正解的思路想很容易想明白，但是想要自己推出来会非常混乱啊。

首先把所有点的 \(t_i\) 全部 \(\bmod 2L\)，把多的圈数累计上。注意到进入每个点所花费的时间与方向是相互独立的，对于一个点来说，从左边进入可能从左边出也可能从右边出，而从右边出时一定是经过了 \(2L\) 的距离，从左边出一定是经过 \(2 (L - x_i)\) 的距离。从右边同理。于是对于每一个点，我们可以计算出它从左边入能否从左边出，以及从右边入能否从右边出，记为 \(revl_i, revr_i\)。首先如果 \(revl_i = revr_i = 0\)，那么这个点经过它只能不改变方向且增加 \(2L\) 的距离，可以先把这部分统计掉。同时，对于 \(revl_i + revr_i = 1\) 的点来说，注意到从不同方向出可以改成从相同方向出，一定不会使得距离更长，所以现在实际上只有三类点，一种是可以从任意方向翻折的点，一种是只能向左或向右翻折的点，问题转化成从左边界开始，每次可以碰到一个翻折点进行翻折，然后可以在左边界和右边界进行任意次翻折，最小化翻折的总次数（最后距离就等于翻折总次数加 \(1\)）。

得到这个还是不太好做，不过可以注意到一个性质：对于 \(revl_i = 1, revr_i = 0\) 的点来说，一定有 \(x_i < \frac L2\)，同理 \(revl_i = 0, revr_i = 1\) 的点也一定 \(x_i > \frac L2\)，那么实际上只能向左翻折的点一定在左半部分，向右翻折的点在右半部分，那么容易想到直接让向左翻折的贪心的向左边找到一个向任意方向翻折的点翻折回去，右边的同理，匹配不上的就从边界翻折，然后此时会剩下若干任意方向的，容易发现可以左右左右不重复的到达所有点。需要注意的是 \(n\) 号点可以直接作为右端点，可以少一次到右边界的次数。

2024.6.18

傻逼 nfls 模拟赛题给我整破防了。T1 和 T2 一共做了一个小时，还不给大样例，然后 corner case 一个包放一个，T2 直接 \(0\) 分，多么好玩。T3 我开场就在做，写完后喜提 \(0\) 分。大样例全过了，不过大样例指 \(n=20\)，而且非常精心的使得每两族之间只有一次交换，所以他妈的我交换次数式子推假了根本看不出来，因为根本没有额外交换，哈哈。我赛时想的是先把所有族位置全部调整正确，然后再调整族间的顺序，虽然发现前者的式子假了（我不知道能不能做？可能推一些比较复杂的式子是能做的，但是可能就比正解的做法还麻烦了），但是傻逼样例族的位置已经排好了所以他妈的根本看不出来。傻逼。

AGC023D Go Home

有趣题，还挺简单的，但是还是想不到，，

发现这玩意根本无法考虑，可以倒过来想。对于最后经过的位置，一定是 \(1\) 或者 \(n\) 中的一个。那么如果 \(p_1 \ge p_n\) 那么最后一定先到 \(1\)，否则先到 \(n\)。证明比较容易。那么此时实际上 \(n\) 只能想让 \(1\) 尽可能早到家，那么此时 \(n\) 一定会选和 \(1\) 一样的决策。那么我们可以把 \(p_n\) 加到 \(p_1\) 上去，然后缩减到 \([1, n - 1]\) 的子问题。\(p_1 < p_n\) 的情况是一样的。可以继续这样做下去。当某一时刻 \(s < x_l\) 或者 \(s > x_r\) 时，肯定是朝这个方向一直走下去，这就是终止条件。

2024.6.19

好焦虑啊怎么办？？？？

然后又摆了一天怎么办？？？？

AGC027E ABBreviate

好厉害啊！！！我咋只会第一步

首先可以把 \(a\) 看做 \(1\)，\(b\) 看做 \(2\)，在 \(\bmod 3\) 意义下考虑，容易发现这样操作一次后整个串的和不变。然后后面我就啥都不会了，菜。

考虑最后得到的串一定是原先串的某些划分，那么我们考虑如何判定一个字符串能否缩减成一个字符，且判定这个字符是啥。判定字符是容易的，因为有上述性质。对于能否缩减成一个字符，有结论：如果一个串和不为 \(0\)，且存在两个相邻相同的字符或长度为 \(1\)，那么就一定可以缩减成一个字符。容易归纳证明，任意时刻要不然一定存在形如 \(abb\) 的子串，操作后仍然存在相邻相同，要不然全部相同，此时也容易发现操作完后要不然只剩一个字符，要不然仍然存在两个相邻相同字符。

首先把一开始就没法操作的情况判掉。那么现在考虑如何确定这个串能否划分成某个串。自然想到贪心匹配，但是手模一下会发现这样会剩下一段和为 \(0\) 的串。不过这个其实是容易调整到一个合法方案的，先把剩下的部分和最后一个串合并，如果合法了就一定可以了，否则一定形如 \(abababa\) 一类的，可以把最后一个字符单独分一组，再把剩下的部分和前面合并。容易发现这样进行下去一定能够存在合法情况。

实际上如果这样分析的话，还可以发现，我们甚至都不需要让前面划分的部分满足内部存在相邻两个相同，因为上述调整法可以对任意一段进行调整，所以实际上只需要满足每一段的和不等于 \(0\) 即可。然后现在要统计本质不同的划分种数，这个就是容易的了，钦定每次划分必须在和相等的前缀中选取最短的划分，这样就能保证不重不漏了。

P10004 [集训队互测 2023] Permutation Counting 2

这玩意疑似有点太神秘了

如果只有一维限制应该是类似于欧拉数的一个东西，不过我没了解过任何欧拉数的性质，而且这题好像跟欧拉数也没关系。

恰好 \(x, y\) 个上升不好做，考虑二项式反演一手，先计算钦定 \(x, y\) 个上升的方案数。

首先转化一步，钦定 \(x\) 个上升即钦定 \(n-x\) 个上升段，我们转而统计上升段的数量。

那么我们设 \(g_{x, y}\) 表示钦定有 \(x\) 个排列上升段，\(y\) 个逆排列上升段的排列方案数。

然后有一个非常厉害的性质：如果我们知道了每个排列上升段和逆排列上升段之间的交的大小，那么我们就能还原出整个排列。设 \(a_{i, j}\) 表示第 \(i\) 个上升段和第 \(j\) 个逆排列上升段的交的大小，首先我们可以知道每个上升段 \(i\) 的长度为 \(\sum_j a_{i, j}\)，每个逆排列上升段 \(j\) 的长度为 \(\sum_i a_{i, j}\)。我们可以依次考虑第一个逆排列与每一个正排列上升段的交，注意到交一定是每个正排列的一个前缀，于是我们就可以确定这些位置填什么，依次考虑每一个逆排列上的上升段即可得知整个排列。

那么我们就得到了一种双射关系：对于一个 \(x \times y\) 的二维数组 \(a_{i, j}\)，满足 \(\sum_j a_{i, j} > 0\) 且 \(\sum_i a_{i, j} > 0\)，并且 \(\sum a_{i, j} = n\)，那么这个二维数组可以与一个排列的钦定上升段与逆上升段的顺序一一对应。设钦定上升的答案为 \(f_{x, y}\)，容易容斥得到：

\[f_{x, y} = \sum_{i \le x} \sum_{j \le y} (-1)^{x-i+y-j} \binom{x}{i} \binom{y}{j} \binom{n+ij-1}{ij-1} \]

直接计算是 \(O(n^4)\) 的，注意这个式子很多地方都是贡献独立的，可以先计算出辅助数组 \(h_{i, y} = \sum_{j \le y} (-1)^{y-j} \binom{y}{j} \binom{n+ij-1}{ij-1}\)，再计算 \(f_{x, y} = \sum_{i \le x} (-1)^{x-i} \binom{x}{i} h_{i, y}\)，这样复杂度就是 \(O(n^3)\) 的。

最后统计答案是一个类似的形式，同样做法即可做到 \(O(n^3)\)。

2024.6.20

摆摆摆。

P7214 [JOISC2020] 治療計画

整个脑子就是不知道在干啥。

可以直接在二维坐标系下考虑，考虑最后不能被感染的村民长什么样子。首先对于一次治疗来说，发现相当于是将一个斜着的正方形内的所有点全部治疗了，而如果有两个正方形有交，那么他们更大的一个并应当都能够被治疗。同时我们一定有 \(l=1\) 或者 \(r=n\) 的治疗，而 \(l=1\) 的治疗相当于一个点向左边的一个斜着的 2-side 矩形内全部治疗。那么实际上我们可以发现，我们就是要选出若干个这样的矩形，使得能够将上下两部分割开，也就是实际上要找从左边到右边的一条最短路。注意到我们每一时刻实际上都是能够治疗一个向左边的一个斜着的 2-side 矩形，有时候会存在多个，这时候可以只保留其中一个矩形也是可以的，这也保证了我们要做的实际上就是最短路。

总之就是可以发现如果 \((r_i, t_i)\) 向左方的 2-side 矩形和 \((\frac{l_j + r_j}{2}, t_j)\) 为中心的一个斜着的正方形有交，那么就可以从 \(i\) 走到 \(j\)。再仔细推一下发现条件就是 \(r_i - l_j \ge |t_i - t_j|\)。注意到这是一个点权最短路，可以发现一个点在跑 dijkstra 的时候，第一次被松弛的时候就是到这个点的最短路，于是我们实际上可以使用一个均摊的算法来找到所有可以得到的点。然后把绝对值拆开，可以得到一个 \(r_i - t_i \ge l_j - t_j, t_i \ge t_j\) 和 \(r_i + t_i \ge l_j + t_j, t_i < t_j\)，可以以 \(t_i\) 为下标，维护 \(l_j - t_j\) 和 \(l_j + t_j\) 的最小值，不断删掉区间内的最小值即可。

CF1682F MCMF?

简单题

首先换个建模，考虑直接把所有点排成一条线，两个点直接连双向权值为 \(a_i - a_{i-1}\) 的边。然后容易发现两条流之间不能相交，然后还因为入度等于出度，最后一定全部匹配掉，那么显然就是从左往右贪心匹配。

考虑怎么快速计算答案，直接考虑每条边有多少流量，设 \(b\) 的前缀和为 \(p\)，容易发现 \(i\) 到 \(i+1\) 边上的流量就是 \(|p_i - p_{l-1}|\)，所以就是要求 \(\sum_{i=l}^{r-1} |p_i - p_{l-1}| (a_{i+1} - a_{i})\) 即可，二维数点容易做。

P7026 [NWRRC2017] Hidden Supervisors

kaguya 题

img

img

img

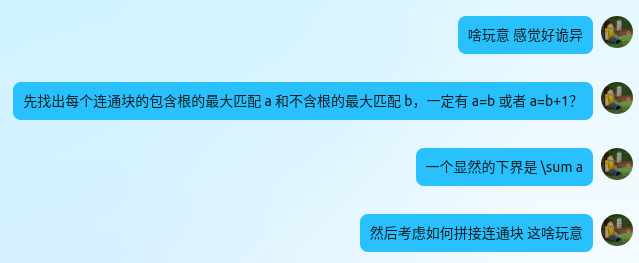
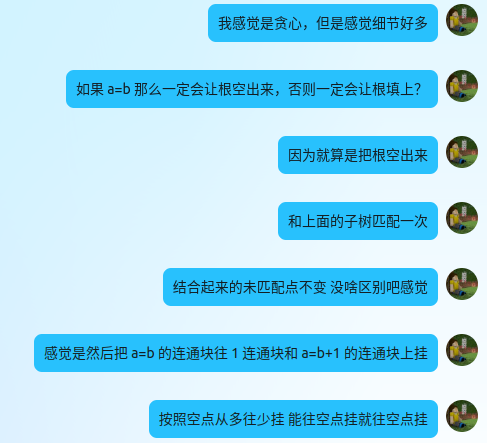
kaguya 说这是对的，我也懒得写了，直接放这里了

2024.6.21

nfls 模拟赛，不知道为啥感觉 T1 巨大困难（虽然好像做法 1.5h 左右就想出来了，但是写加调试快 1.5h 了，而且想 1.5h 好像也挺长的），但是 T2 半小时过了，，

T3 和我赛时猜的做法差不多，但是那玩意太原神了，纯纯恶心人题，然后就写暴力开摆了。然后暴力还挂了，因为求 height 的时候会和 s[n + 1] 的位置比较，然后 s 没清空所以炸了，，

怎么有一种 nfls 模拟赛没活整了的感觉，成天放一些好题

P7670 [JOI2018] Snake Escaping

啥玩意，这我想不到？？？

正经做法：考虑对 0, 1, ? 的个数讨论，如果 ? 最少可以直接暴力。否则，我们可以进行一步容斥，比如 0 就是让 ? 减去 1 的个数，这样我们要问的就是只包含 0 和 ? 或者只包含 1 和 ? 的问题，然后高维前缀和容易做。三个取 \(\min\) 即可做到时间复杂度 \(O(q 2^\frac L3 + 2^L L)\)。

更加暴力的做法：考虑暴力枚举 \(k\) 位，剩下 \(L-k\) 位预处理，复杂度 \(O(q 2^k + 2^k 3^{L-k})\)。当然不能直接全处理出来，空间开不下，直接离线下来对每个 \(2^k\) 做一遍即可，预处理每次转移 lowbit，三进制 lowbit 可以预处理。取 \(k=7\) 最优。

AGC023F 01 on Tree

好像是个经典贪心题

有一个显然的观察，就是有 \(0\) 一定选 \(0\)。然后我们注意到我们肯定会尽可能多选 \(0\)。可以考虑树上贪心的一个经典做法，每次找到全局最优值，然后把它和父亲合并。考虑两个连通块之间的先后顺序，容易发现就是在优先选 \(\frac{cnt_0}{cnt_1}\) 较小的。然后贪心就好了。

2024.6.22

nfls 模拟赛，没挂分，舒服。

T1 是去年某一时刻的旧 acc 上考过的题，等我推完做法了才想起来好像确实做过这题。哈哈。

T3 给我 cpu 干烧了。虽然好像是个比较简单的贪心。

争取到了放假的机会，哈哈，下周六放假。

明天神秘欢乐 ACM 赛。但是单人打，火大。

T3 天接云涛连晓雾

有两个数组 \(a\) 和 \(b\)，你可以进行若干次操作，使得 \(a\) 数组与 \(b\) 数组相等：

  • 对 \(a\) 数组中 \([l, r]\) 内 \(> 0\) 的位置加 \(1\)；
  • 对 \(a\) 数组中 \([l, r]\) 内 \(> 0\) 的位置减 \(1\)。

最小化操作次数。

\(n \le 10^6,\ a_i, b_i \ge 0\)

首先把无解判掉，只有 \(a_i = 0, b_i \ne 0\) 的时候会无解。

直接对区间操作肯定是不好刻画方案的，自然考虑从 \(1\) 扫到 \(n\) 时每个位置的加减区间数。首先注意到，如果存在某个位置先被加，再被减，那么一定可以把相交的部分给去掉，拆成两次不相交的操作。也就是说，每个位置一定先被减后被加。于是我们其实可以用两个数来记录方案：\(x, y\) 表示从前面引过来 \(x\) 条 \(-1\) 的线段，\(y\) 条 \(+1\) 的线段。那么这一步会进行的操作就是会把 \(x, y\) 变化为 \(x', y'\)，贡献为 \(\max(x' - x, 0) + \max(y' - y, 0)\)。发现 \((x, y)\) 只有 \(O(n)\) 对，于是到这里就可以得到一个约 \(O(nV^2)\) 的 DP 了，应该可以拿到一些分数。

考虑继续分析操作。观察我们能决策什么。比如我们需要减少当前的数时，我们可以选择将一个 \(+1\) 段给删掉，或者增加一段 \(-1\) 段。当前来看肯定是删段更优，因为此时不会造成额外贡献，但是可能到后面会发现改成加段更优，因为这时候 \(+1\) 段和 \(-1\) 段都会多一段。那么我们可以记录一个 \(z\) 表示当前有多少这样的选择可以修改，使得 \(-1\) 段和 \(+1\) 段都多 \(1\)，且花费 \(1\) 的代价。这样我们就可以用 \((x, y, z)\) 来表示当前的状态。这类似于一个反悔贪心的过程。

接下来就可以考虑贪心了。贪心分两步来做，首先我们先进行调整，使得之后 \(z\) 一定能够合法（即 \((x + k, y + k), k \in [0, z]\) 都能够合法），然后再贪心选贡献最小的方案。分 \(b_i = 0\) 还是 \(\ne 0\) 来讨论。

  • \(b_i > 0\)：
    我们先进行一些调整：首先必须有 \(x \le a_i - 1\)，否则就会被减到 \(0\)。如果 \(x > a_i - 1\)，那么就需要把 \(x\) 进行缩减。同时，因为 \(x + z\) 也不能超过 \(a_i + 1\)，所以这时候还需要将 \(z\) 与 \(\max(0, a_i - x - 1)\) 取 \(\min\)。同理，一定有 \(y \le b_i - 1\)，可以用上面同样的方法对 \(y\) 与 \(z\) 进行缩减。这样之后，之后无论对 \(z\) 进行任何操作后，当前位置仍然能保持合法。（对 \(y\) 也要限制的原因是，如果不对 \(y\) 限制，那么 \(y\) 在反悔时也可能会使得 \(x\) 增加，从而导致不满足条件。）

    然后要考虑如何调整，只需要按照先删区间，如果区间数不够则用 \(z\) 同时加 \(x\), \(y\) 区间，如果还不够再单独加对应的 \(x\) 或者 \(y\) 区间。删区间时对应的要把 \(z\) 进行增加。显然这样的选用顺序是最优的。

  • \(b_i = 0\)：
    此时只需要满足能够减到 \(0\) 即可，也就是 \(x \ge a_i\)，类似的思路，先用 \(z\) 补再单独加。

总时间复杂度 \(O(n)\)。

2024.6.23

img

cool

中间平均 10~20 min 过一题，开头和结尾过题较慢，鉴定为没睡醒与想题想困了。

好像在原榜上拿 rk1 了，哈哈

A. Eminor Array

有点大力的题感觉，，

考虑什么时候出现三个数异或等于 \(0\)，考察 \(a_{i-1}, a_i, a_{i+1}\) 的最高位，注意到如果 \(a_{i-1}, a_i\) 的最高位相同，那么如果想要三个数异或等于 \(0\) 则 \(a_{i+1}\) 就一定比 \(a_i\) 小了，所以此时 \(a_{i-1}\) 和 \(a_i\) 最高位一定不同，同理可以得到 \(a_i\) 和 \(a_{i+1}\) 最高位一定相同。设 \(a_{i-1}\) 的最高位为 \(p\)，\(a_i\) 和 \(a_{i+1}\) 的最高位为 \(q\)。

继续考虑，考虑 \(a_i\) 上的第 \(p\) 位，如果这一位是 \(1\)，那么 \(a_{i+1}\) 上这一位就等于 \(0\)，而 \(p+1 \sim q\) 位又得相等，于是大小关系又被破坏了，所以一定有第 \(p\) 位为 \(0\)，那么 \(a_{i+1}\) 的第 \(p\) 位就是 \(1\)。由此我们可以得出一个想法：每次填若干最高位等于 \(q\) 的数，设 \(f_q\) 表示最后一段数最高位为 \(q\) 的方案数，然后转移即可。

考虑填一段数的方案是多少。不合法的情况上述已经讨论过了，注意到我们如果确定了 \(a_{i+1}\) 是什么之后，如果异或和相等，那么 \(a_i\) 也就确定了，所以我们只需要枚举 \(a_{i+1}\) 是什么就行了，需要满足他的 \(p\) 二进制位为 \(1\)。然后就没有别的限制了，大概是 \(f(p, q) = \sum_{x=0}^{2^{q-p-1} - 1} \sum_{y=0}^{2^p - 1} 2^{2^q - 1 - x 2^{p+1} - y - 2^p}\)，可以等比数列求和化出式子，然后 \(p\) 和 \(q\) 的贡献可以拆开，于是就可以 \(O(n)\) 转移 DP 了。

H. Games on the Ads 2: Painting

这题居然场上没人过。我想加写花了 20 min，哈哈。

很好奇在这样的线下打时榜会不会对人的做题策略有很大的影响。

注意到题目中给到的限制实际上就是，对于一个格子来说，如果其颜色与这一行颜色相同，那么这一列必须比这一行先操作，否则这一行必须比这一列先操作，而颜色相同的操作之间没有顺序。

这实际上是一个拓扑序计数，虽然 \(n \le 20\) 但是直接建图是 \(2n\) 个点，直接跑也是跑不了的。注意到这张图是一个二分图，且几乎是满的，只有 \(n\) 条边不存在。假如是一个满二分图，那么 DAG 一定是分层的，且注意到相邻两层之间一定两两有边，于是实际上我们只能每次选完整层点然后再选下一层点，于是拓扑序数量就是每层点的阶乘的成绩。那么剩下的部分就显然了，我们实际上只需要把不存在的 \(n\) 条边枚举一下定向，然后做满的拓扑序计数就行了，复杂度 \(O(2^n n^2)\)。

upd. yswn 太厉害，考虑到最后分层图的形态，实际上还可以直接按照右部点的入度大小进行排序，即可得到 \(O(n)\) 的做法。

K. String Divide II

心心念念了好久的 trick 终于用上了一次。

如果我们能够找到某个串的相邻两次出现位置，那么我们就可以通过求最长公共后缀来直接得到这个串重复出现了多少次（即我们可以找到一个 border，即周期，于是就可以知道出现多少次）。我们实际上只需要关心同一个串的相邻两次出现位置，而实际上一个串相邻两次出现位置只有 \(O(n \log n)\) 的，因为我们可以通过 SAM 启发式合并维护 endpos 集合的过程得到 \(O(n \log n)\) 个相邻点对。但是实际上最终答案中的重复 \(k\) 次的串有可能两次出现并不是相邻的（比如 abab|abab 中 abab 实际上出现了三次，这两次出现并不相邻），但是这样一定能将这个串划分成更短的相等的串，所以实际上我们只需要考虑所有相邻两个位置的串，然后对于这些串看他们最多重复了多少次，然后把它们划分成相等的 \(k\) 部分就能得到一个重复 \(k\) 次的串了。

具体实现上，找 \(O(n \log n)\) 个相邻对可以通过线段树合并在 \(O(n \log n)\) 的时间复杂度内求出来，具体就是合并两个子树后将左子树内最大值与右子树内最小值作为一对即可。但是这种做法在本题会 MLE，不过时限开的很大，所以直接写 \(O(n \log^2 n)\) 的 set 启发式合并也可以。对于求最长公共后缀来说，实际上可以发现相邻两对直接在 fail 树上的 lca 就是统计到这对位置的时候的那个点，所以直接拿当前点的长度作为最长公共后缀即可，这样肯定只会得到更短的答案，不会得到更优的错误答案。

2024.6.24

保序回归是啥啊，，

T5 整一二元 gf \(\ln\) 题，我想到做法了懒得写（

保序回归学习笔记

给一个 DAG 图，满足 \(u \to v\) 表示 \(f_u \le f_v\)，求一个序列 \(f\) 使得最小化 \(\sum w_i |f_i - y_i|^p\)，其中 \(p \ge 1\) 称做保序回归的阶，称为 \(L_p\) 问题。

证明全部咕掉，直接写下做法，我反正是快退役的人了。

定义 \(L_p\) 均值为使得 \(\sum w_i |x - y_i|^p\) 取得最小值的 \(x\)，可以证明 \(p >1\) 时 \(L_p\) 均值是唯一的，并且对于 \(L_p\) 问题来说，一定存在一组最优解 \(f_i\) 使得每个 \(f_i\) 都等于某个子集的 \(L_p\) 均值。这里给出 \(L_1\) 为 \(y_i\) 的带权中位数，\(L_2\) 为 \(y_i\) 的带权平均数。

有引理：对于一个子问题 \((A, B)\) 表示若限制 \(f_i \in [A, B]\) 时的 \(L_p\) 问题，若满足任意子集的 \(L_p\) 均值均不在 \((A, B)\) 中，那么设该问题的一组最优解为 \(f'_i\)，那么一定存在一组原问题的最优解 \(f_i\)，使得当 \(\forall f'_i = A, f_i \le A\)，且 \(\forall f'_i = B, f_i \ge B\)。且容易发现这个子问题存在最优解满足 \(f'_i \in \{A, B\}\)。

于是可以考察一个类似于整体二分的算法，设计递归函数 \(\mathrm{solve}(S, l, r)\) 表示考虑点集 \(S\) 的 \((l, r)\) 子问题的解，我们可以找到一个极小的区间 \((mid, mid + \varepsilon)\) 求得它的最优解，然后按照最优解将 \(S\) 划分成两个集合 \(P, Q\)，满足 \(P\) 集合内的 \(f'_i = mid\)，即 \(f_i \in [l, mid]\)，且 \(Q\) 集合内的 \(f'i = mid + \varepsilon\)，即 \(f_i > mid\)，但是由于我们要让 \(\varepsilon\) 足够小所以还是直接认为 \(f_i \ge mid\)。那么我们直接递归调用 \(\mathrm{solve}(P, l, mid)\) 和 \(\mathrm{solve}(Q, mid, r)\) 就行了。但是直接找一个 \(\varepsilon\) 使得符合上述引理条件是困难的，考虑修改一下贡献，当前选 \(mid + \varepsilon\) 比选 \(mid\) 的贡献多 \(w_i |mid - y_i|^p - w_i |mid + \varepsilon - y_i|^p\)，通过给所有权值除以 \(\varepsilon\) 后，再令 \(\varepsilon \to 0\)，那么贡献实际上是 \(\lim_{\varepsilon \to 0} \frac{w_i |mid - y_i|^p - w_i |mid + \varepsilon - y_i|^p}{\varepsilon} = (w_i |x - y_i|^p)'\mid_{x=mid}\)，直接把贡献设为这个即可。\(L_1\) 中为 \(w_i \cdot \mathrm{sgn}(mid - y_i)\)，\(L_2\) 中为 \(2 w_i (mid - y_i)\)。求解子问题实际上是一个最大权闭合子图的问题，在一般图上可以直接跑最大流，特殊图上（比如树）可以考虑用其他方法解决。

如果限制 \(f_i\) 是整数的话，那么也就限制了 \(L_p\) 均值是整数下的均值，于是实际上只需要直接拿 \((mid, mid + 1)\) 来做就行了，因为这个区间内显然不会存在任何一个正整数，这样直接用原来的函数作为贡献也是可以的。

ref

2024.6.25

nfls 模拟赛，快恶心死了，T2 阴间玩意还要写类欧，不会推类欧就直接贺了个万欧板子，然后调到 1:05 多才过，，恶心爆了

CF1307G Cow and Exercise

好题啊！！！

这玩意的方案看着就很复杂，考虑用线性规划来描述这个问题。最短路是可以用差分约束来描述的，即给每个位置设一个 \(d_u\)，满足 \(d_v \le d_u + w_{u, v}\)，那么 \(d_n - d_1\) 的最大值就是最短路了。我们要最大化最短路，也就是考虑每条边被增加的量 \(a_{u, v}\) 满足 \(d_v \le d_u + w_{u, v} + a_{u, v}\)，那么就可以写出线性规划的形式了：

\[\begin{array}{cc} \text{maximize } & d_n - d_1 \\ \text{ s.t.} & \begin{cases} d_v \le d_u + w_{u, v} + a_{u, v}\\ \sum a_{u, v} \le x\\ d_u, a_{u, v} \ge 0 \end{cases} \end{array} \]

这就是一个很标准的线性规划的形式了。套路地，考虑写出其对偶：

\[\begin{array}{cc} \text{minimize } & p x + \sum q_{u, v} w_{u, v} \\ \text{ s.t.} & \begin{cases} \sum_i q_{i, u} - \sum_i q_{u, i} \ge 0 & \forall u \in (1, n)\\ \sum_i q_{i, 1} - \sum_i q_{1, i} \ge -1\\ \sum_i q_{i, n} - \sum_i q_{n, i} \ge 1\\ p \ge q_{u, v}\\ p, q_{u, v} \ge 0 \end{cases} \end{array} \]

注意到最优解中 \(d_i\) 显然可以全部 \(> 0\)，根据互补松弛性，这些条件都是取等的，且 \(p\) 显然会取最小值，即 \(p = \max a_{u, v}\)，于是可以写成：

\[\begin{array}{cc} \text{minimize } & p x + \sum q_{u, v} w_{u, v} \\ \text{ s.t.} & \begin{cases} \sum_i q_{i, u} - \sum_i q_{u, i} = 0 & \forall u \in (1, n)\\ \sum_i q_{i, 1} - \sum_i q_{1, i} = -1\\ \sum_i q_{i, n} - \sum_i q_{n, i} = 1\\ p \ge q_{u, v}\\ p, q_{u, v} \ge 0\\ \end{cases} \end{array} \]

注意到这很像一个最小费用最大流的问题，考虑转化一下。此时还有一个 \(p\) 很丑，考虑 \(p\) 实际上是限制了所有的流量上界，考虑让流量全部除以 \(p\)，即令 \(q_{u, v} \gets \frac{q_{u, v}}{p}\)，那么就可以得到：

\[\begin{array}{cc} \text{minimize } & \dfrac{x + \sum q_{u, v} w_{u, v}}{\frac 1p} \\ \text{ s.t.} & \begin{cases} \sum_i q_{i, u} - \sum_i q_{u, i} = 0 & \forall u \in (1, n)\\ \sum_i q_{i, 1} - \sum_i q_{1, i} = -\frac 1p\\ \sum_i q_{i, n} - \sum_i q_{n, i} = \frac 1p\\ q_{u, v} \in [0, 1] \end{cases} \end{array} \]

这时候把 \(\frac{1}{p}\) 看做流量 \(flow\)，那么上面的限制就是一个标准的最小费用最大流了，而 \(\sum q_{u, v} w_{u, v}\) 就是费用，记作 \(cost\)，那么我们实际上就是要找到一个流量 \(flow\)，使得最小化 \(\frac{x + cost}{flow}\)。容易发现 \(flow\) 只有 \(O(n)\) 种，于是直接跑最小费用最大流之后直接枚举即可，复杂度 \(O(n^2m + nq)\)。

2024.6.26

讲课，图论，讲了一堆科技和一些神秘杂题。杂题没听，可能会自己做做。

CF1519F Chests and Keys

观察题意，太好了啊！不会做。

仔细思考一下，Bob 赢不了的条件是什么，那么也就是说对于 Bob 想要开的任意一个箱子集合，买这些箱子需要的钥匙的钱都大于等于箱子的钱。惊人的发现，这不就是 Hall 定理吗！改成二分图匹配的形式，左部点是箱子右部点是钥匙，匹配次数上限就是钱数。那么问题就是加入最少代价的边使得左部点能够匹配满，由于 \(n, m\) 和值域都很小，可以直接把左右部点的流量压成状态，直接搜索，每次加入一条边，然后把能匹配的全匹配上即可。复杂度不知道，反正不大，不超过 \(O(n^2 5^{2n})\)，而且很多装态都达不到，随便过。

2024.6.27

下午和晚上在 OIer Bot 群 加训 我不喜欢你，海龟汤，英语单词接龙，饲养小猫

啥玩意，你们 OIer 成天都玩这么无聊的东西？？？

P8519 [IOI2021] 钥匙

昨晚上想到了个做法，然后早上写完发现假了，然后吃饭的时候想到了一个做法，感觉很炸裂但是感觉是对的，然后写了一上午，缝缝补补调半天，最后摆烂了去 loj 下数据了才调出来，，不过算是自己做出来的（？）但是感觉这题很有趣啊！

首先有一个显然的性质：记 \(S_u\) 为从 \(u\) 开始能够到达的集合，那么对于 \(v \in S_u\)，一定有 \(S_v \subseteq S_u\)，由于我们要找 \(|S_u|\) 最小的 \(u\) 集合，且如果 \(S_u\) 是极小的，那么这个集合内的 \(v\) 应当都满足 \(S_v = S_u\)。那么实际上如果知道 \(u\) 能够到达 \(v\)，那么我们只需要考虑 \(v\) 的 \(S_u\) 即可。

先考虑一些简单的情况。考虑每个点是否有相邻的 \(c = r_u\) 的边，如果有则把这条边当做这个点的出边，假如存在一个点没有出边，那么这个点一定就是 \(S_u = \{u\}\)，且是最小的了，可以直接得到答案，否则，每个点一定都存在出边，那么这形成了一个基环树森林，根据前面的分析，我们只需要考虑每个基环树森林的环上的点即可。但是显然环上的点并不就完全等于 \(S_u\) 了，因为此时从这个环出发可能还能到这棵基环树上的其他点与其他基环树上的点。我们可以先在这棵树的环上模拟一次这个过程看看能够到达这棵树上的哪些点，但是这样之后就不能给我们更多信息了，因为还有可能从这个点到其它基环树上，再回来后可能能达到的点会更多。可以一直迭代下去模拟，但是直接这样模拟显然复杂度就没有任何保证了。

考虑实际上我们每一时刻在维护若干类似于连通块的东西，且如果能从到达别的基环树再回来那么这相当于把若干连通块合并了起来。可以考虑一个类似于 Boruvka 算法的思想，每次模拟一遍找到这个连通块向外的一条连边，然后再用这样的连边把连通块之间连成一个基环树森林，把在同一棵基环树内的连通块合并。这样根据和 Boruvka 一样的分析方法发现每轮下来连通块数减半，直接这样模拟就能 \(O((n+m) \log n)\) 解决。但是注意到可能会存在时刻使得一个连通块不存在出边，那么显然这时候这个连通块就是一个极小的 \(S_u\) 了，我们就可以把它给除去。这其实类似于一个强连通分量缩点的过程，把不存在出边的连通块直接删掉，相当于是这个连通块就是一个强联通分量了。当然有可能出现删除一个连通块后剩下的某些连通块又不存在出边了的情况，我们只需要模拟的时候找到所有出边，然后把出边建出一张图，对这张图拓扑排序一下就能知道哪些连通块需要被删除，然后再把删不掉的分成基环树森林，一棵基环树内的连通块全部合并即可。

模拟是容易的：维护一下当前有哪些钥匙，和没有对应钥匙但是访问过的边，拿到对应钥匙时把当前点的出边与之前访问过但是正好需要这把钥匙的出边全遍历一遍，跑个 BFS 即可。

P5811 [IOI2019] 景点划分

唉，为啥想不到，为啥想不到，为啥想不到，为啥想不到。少学烂七八糟的东西，想双极定向想了一年。

先把 \(a, b, c\) 从小到大排序，显然令 \(a, b\) 为联通的不劣。重要性质是 \(a \le b \le \frac n2\)，显然。

树肯定是找一条边断开使得一个连通块 \(\ge a\) 另一个连通块 \(\ge b\)。更细致的考虑，发现如果存在方案那么一定存在方案断的边一个端点在重心，这样较大的连通块一定 \(\ge \frac n2 \ge b\)，且较小的连通块也是 \(\le \frac n2\) 的极大连通块。

考虑图上，找 DFS 树后，仍然可以先找是否存在 \(\ge a\) 的子树，如果有就直接构造完了。否则，此时所有子树 \(< a\)，注意到是 DFS 树，只有返祖边，那么向下的子树之间不存在连边，那么如果存在方案一定是向父亲方向的子树与向下的几个子树连通。注意到所有子树 \(<a\)，那么我们可以挨个加入每个父亲方向子树连通的子树，那么最多也就额外占用 \(a\) 个点，也就是不超过 \(2a\) 个点，由于 \(a \le b \le c, a + b + c = n\)，这样剩下的点数一定仍然大于等于 \(b\)，所以直接再从根 DFS 一下就行了。全加入了都不足 \(a\) 则肯定不合法，因为可以注意到无法被加入的子树与重心相连的边为割边，若想要和它连通一定和重心连通，然后就不存在 \(\ge b\) 的连通块了。

P7054 [NWRRC2015] Graph

似乎是简单贪心

考虑加一条边能干什么，假如在拓扑排序的时候，此时有多个点可以选，那么我们会贪心的想让最小值不能被选。注意到其实加一条边对拓扑排序的过程的影响仅仅是让一个点入度加 \(1\)，使得他当前不能被选，所以这条边的起点是不重要的，于是我们可以先钦定一个点不能被选，等到需要这个点需要作为 \(p_i\) 被选时，加一条从 \(p_{i - 1}\) 向 \(p_i\) 的边，这样就能限制这个点恰好在这个时刻才能够被选。那么现在只需要一个简单贪心就够了，如果有多个点备选则尽可能每次禁用最小值，如果只有一个点时，考虑将一个禁用的点用在这里是否会更优，如果用禁用点更优则可以将当前点禁用并使用最大的禁用点，否则就直接用当前点。如果没有点可选就选一个最大的禁用点。可以用一个小根堆维护拓扑排序和一个大根堆维护禁用点即可。

2024.6.28

模拟赛爆蛋拉！

C Procyon

先考察具体要满足什么，注意到对于一个区间来说，如果一个 \(a\) 合法，那么一定也就能唯一确定其对应的 \(b\)，所以我们只需要维护每个区间内合法的 \(a\) 即可。先考察限制的形式，对于区间 \([l, r]\) 来说，令 \(y_i = x_{r - (i - l)}\)，即翻转后的位置，那么有方程组 \(a x_i + b \equiv y_i\)。由于我们只关心 \(a\)，考虑将这个方程组差分一下，这样就得到了仅对 \(a\) 限制的方程组，即 \(a (x_{i - 1} - x_i) \equiv y_{i - 1} - y_i\)，直接解一下这个线性同余方程，可以得到这个方程的解集。注意到解集一定可以表示成 \(a \equiv b \pmod p\) 的形式，其中 \(p\) 是 \(P\) 的一个因子。那么整个串的解集就是把每个方程的解集的交，直接 excrt 一下即可合并解集。

现在考虑如何维护这些解集。考虑这个东西看着就很像回文的形式，可以用 Manacher 网上套一下看看有没有类似的性质。假设对于一个大区间 \([1, n]\) 是 \((a, b)\) 回文的，那么如果有一个子区间 \([l, r]\) 是 \((a', b')\) 回文的，那么有 \(a' x_l + b' = x_r, a x_l + b = x_{n-l+1}, a x_r + b = x_{n - r + 1}\)，带入可以得到 \(a (a' x_l + b') + b = x_{n - r + 1}\)，整理可以得到 \(a' (a x_l + b) - a' b + a b' + b = x_{n - r + 1}\)，即 \(a' x_r - a' b + a b' + b = x_{n - r + 1}\)，那么发现此时 \([n - r + 1, n - l + 1]\) 一定也是 \((a', ?)\) 回文的，也就是说 \(a\) 的解集不变，这样我们就容易用 Manacher 的方法维护出来每个中心的区间的解集了。我们可以把 Manacher 的过程建出树，子树求和一下之类的即可得到每个 \(a\) 的解集出现了多少次，用桶维护一下即可。第一类查询的时候直接枚举 \(P\) 的因子，看 \(a \equiv (a' \bmod d) \pmod d\) 的解集有多少即可。

然而第二类查询就不能这么做了，因为 \(b\) 的解集并不满足上述性质，我们需要更近一步挖掘性质。注意到上述过程中，合并时解集要不不变，要不然模数 \(p\) 一定增大，而增大就一定至少翻倍，而 \(p\) 任意时刻也必须是 \(P\) 的因子，那么实际上对于每一个回文中心，其不同的方程仅有 \(O(\log P)\) 种，于是上述 Manacher 过程实际上可以改成直接暴力把上一个回文中心的所有方程复制过来，然后再进行操作就行了，这样得到的总方程个数也就是 \(O(n \log P)\) 级别的。这样我们就可以考虑 \(b\) 的解集了，从每一个位置的 \(a\) 的解集推出 \(b\) 的解集即可，具体来说有 \(b \equiv y - ax \equiv y - (kp + d)x \equiv y - dx - px \cdot k\)，令 \(g = \gcd(P, px)\)（把解集中的 \(b\) 重命名为了 \(d\) 防止重名），那么 \(b\) 的解集就是 \(b \equiv y - dx \pmod g\) 了，注意每个 \(b\) 出现了 \(\frac gp\) 次，所以要把出现次数乘 \(\frac gp\)。然后用同样的方法就能做了。复杂度 \(O(n \log P + q d(P))\)。

2024.6.29

啥玩意，模拟赛有点唐。

T2：计算 \(4^{-n} n \binom{2n}{n}\)。我以为这题不可能直接能化出一个很容易计算的式子就对着 \(\sum\) 的式子想怎么计算，得到一个 Lucas 拆开做数位 DP 的做法。结果告诉我直接硬推一下式子就能得到这个封闭形式了，哈哈。唐。

T3 稍微有点意思，但是意思不多：题是说每次找到矩形内的最大值或最小值，然后删除这个点所在的一行一列，分成四个子矩形继续下去做，第 \(i\) 层删除的最大值还是最小值由 \(a_i\) 给出，最后输出哪些点被删除以及上一层是哪个点。\(nm \le 4 \times 10^6\)，卡空间。注意到每次操作后会删除 \(n+m-1\) 个点，所以实际上只需要在 \(O((n + m) \mathrm{polylog})\) 的复杂度内找到矩形内的最大值或者最小值就够了，所以直接拿线段树再卡卡空间就行了，，官解写的不知道是啥

2024.7.2

额有点摆，口胡个模拟赛吧。明天去重庆。

上午起床发现九点了）然后想了半天不会 T1，构造太恶心，写了个搜发现小点能搜出来但是找不到啥规律，遂摆，要写暴力还得写个高精 crt，滚吧。T2 一标准线性规划形式，随手对偶一下发现问题就是选若干区间使得每个位置重合不超过 \(k\) 次，最大化选择线段的权值和，等价于选 \(k\) 个互不相交的线段集合，发现没啥好做法，发现这东西可以建出费用流，流量只有 \(k\) 于是直接上原始对偶即可，睡之。

我考前应该复习原始对偶吗，算了再说。

T3 酱

有点神秘啊。能猜到是等差数列，然后就不是我能想的东西了。

显然这个东西可以用 PAM 做，但是显然这玩意不可能能带删，弃之。考虑一个更可能拓展的维护方式，众所周知回文后缀形成 \(\log\) 个等差数列，考虑直接增量维护这个回文后缀集合。

考察往后加一个字符，首先会增加一个字符，然后对于每一个等差数列来说，除了最长的那个串以外拓展的可能性是一样的（因为前面的字符都相同），所以容易判断能否拓展，然后直接遍历一遍即可。这样就可以维护出回文后缀集合了。

不过一次只能加一个字符肯定还是做不了任何东西的。我们需要单点修改区间查询，那么我们直接考虑一个更强的结构来做这件事情，考虑用线段树维护后缀回文集合，那么我们就需要支持快速合并两个串的后缀回文集合。

分几种情况讨论：对于合并的两个串 \(S, T\)，考虑其新的回文后缀有几种情况：

  1. 完全在 \(T\) 中；
  2. 一部分在 \(S\) 中，且回文中心在 \(T\) 中；
  3. 一部分在 \(S\) 中，且回文中心在 \(S, T\) 的分界点处；
  4. 一部分在 \(S\) 中，且回文中心在 \(S\) 中。

首先第一种情况就是直接继承 \(T\) 的后缀回文集合。

第二种情况比较复杂。考虑新的后缀相当于是 \(T\) 中的一个回文前缀拓展来的，所以可以同时再维护一下前缀集合，合并方法和后缀是一模一样的。那么我们现在就是要将前缀集合拓展至结尾。

考虑将等差部分设做 \(B\)，那么一个等差数列中的前缀就是 \(A, AB, AB^2, \cdots, AB^k\)。考虑 \(T = AB^K C\)，如果这个等差数列可以进行拓展，那么显然拓展得到的后缀集合也是一个等差数列，那么我们可以尝试将其也写作 \(C' B'^k A'\) 的形式。如果 \(C\) 是 \(B\) 的一个前缀，那么就可以写成这样的形式，那么我们直接考虑可以向前拓展多少即可，直接二分一下。如果 \(C\) 不是 \(B\) 的一个前缀，那么写不成这样的形式，也就是说只可能存在一个这样的串，即 \(C^R (B^R)^{k'} A B^{k'} C\)，同样找到向前最多拓展多少即可知道这个后缀。题解说这部 分精细实现可以单 \(\log\)，虽然我没想明白怎么做到把上面的二分去掉（要对 \(\log\) 个等差数列进行二分？）

第三种情况显然只有一个，直接判即可。第四种情况就相当于 \(S\) 的后缀回文全部拓展一个字符串 \(T\)，和加一个字符的做法差不多（如果 \(|T|\) 比公差大？应该同样是一些后缀的结果相同，剩下的若干个后缀向前拓展的串两两不同，且都形如 \(AB^k\)，判断一下有没有 \(T = AB^k\) 即可）。

总之通过上述讨论，我们可以在 \(O(\log (|S| + |T|))\) 复杂度内合并两个串的后缀集合，直接扔到线段树上维护即可做区间查询。对于单点修改，由于上述操作都需要哈希，可以用一个分块来平衡一下复杂度，做到 \(O(1)\) 查询 \(O(\sqrt{n})\) 修改，这样单次修改复杂度 \(O(\log^2 n + \sqrt{n})\)。

2024.7.4

某集训 day 1，rk2，神秘

T1 感觉很困难啊！虽然每一步好像都很套路的，但是觉得自己推出一整连串的东西还是挺好玩的（

T2 神秘交互，感觉之前应该见过这种东西（甚至应该是考过？但是不记得和这题是不是完全一样了，应该是至少两年前考的），但是场上写了一会发现错误率有点高（我写的固定二分轮数，没想到直接判定最大概率 \(> 1-\varepsilon\) 的时候结束，所以错误率挺高）。但是不太理解怎么动态维护插入排序啊，我岂不是需要支持插入和查询第 \(k\) 大？？？我能 \(O(1)\) 查询第 \(k\) 大不？？？要不然复杂度直接两个 \(\log\) 了，所以场上直接摆了，加上还有两个小时感觉不如紧着去打 T3 暴力。（然后 T3 暴力有个数组开小了挂了，流汗）

唉，还是理性偷税比较有意思，不想写代码，，，

T1 加一2.5

给定一个序列 \(b_i\)，初始有一个全 \(0\) 序列 \(a_i\)，每次你可以对一个前缀加 \(1\) 或者对后缀加 \(1\)，在 \(i\) 处前缀加 \(1\) 的代价是 \(p_i\)，在 \(i\) 处后缀加 \(1\) 的代价是 \(s_i\)，问最少代价使得所有 \(a_i \ge b_i\)。
\(n \le 5 \times 10^5\)

场上有若干厉害贪心做法，我没这脑子只能朴素推了，

首先这玩意长得太线性规划了，写成线性规划随便对偶一手。写一下吧：

\[\begin{array}{cc} \text{minimize } & \sum p_i x_i + \sum s_i y_i \\ \text{ s.t.} & \begin{cases} \sum_{j=1}^i y_j + \sum_{j=i}^n x_j \ge b_i\\ x_i, y_i \ge 0\\ \end{cases} \end{array} \]

对偶一下：

\[\begin{array}{cc} \text{maximize } & \sum t_i b_i \\ \text{ s.t.} & \begin{cases} \sum_{j=1}^i t_j \le p_i\\ \sum_{j=i}^n t_j \le s_i\\ t_i \ge 0 \end{cases} \end{array} \]

这样就只用考虑一个数组了。现在的问题就相当于是对于每个前缀和后缀的和有限制。没什么想法，可以考虑费用流建模，这是容易建出费用流模型的，只需要建两排点分别表示前缀与后缀限制，然后从一排向另一排连费用为 \(b_i\) 的边，就表示流过这个则会使得前缀与后缀的限制减 \(1\)。但是这玩意还是太复杂了，并不好直接模拟，不过这告诉我们一件重要的事情：这个代价是关于 \(\sum t_i\) 凸的。

那么我们就可以直接三分这个 \(\sum t_i\) 了，设它为 \(X\)。原来的限制是前缀和与后缀和的限制，由于知道了总和，我们可以把后缀和的限制变成前缀和的限制了，设前缀和为 \(pre_i\)，那么实际上就是有 \(pre_i \in [L_i, R_i]\) 的限制，容易发现 \(L_i = max(0, X - s_i), R_i = min(X, p_i)\)，同时 \(pre_i \ge pre_{i-1}\)。这样我们就可以得到一个暴力 DP 了，\(f_{i, j}\) 表示 \(pre_i\) 的最大贡献，总贡献为 \(\sum (pre_i - pre_{i-1}) b_i = \sum pre_i (b_i - b_{i+1})\)。容易发现可以直接维护函数，每次前缀 \(\max\) 一下，再加上一个一次函数 \((b_i - b_{i+1}) x\)，最后限制在 \([L_i, R_i]\) 内，这个显然是可以 slope trick 维护的，并且只需要拿一个双端队列就可以维护了，不需要用堆，加上外层三分容易 \(O(n \log n)\) 解决本题。

T2 快速排序

交互，给一个长度为 \(n\) 的排列排序，你每次可以询问两个下标的值的大小关系，交互库有 \(P = 0.1\) 的概率会返回错误答案。

\(n = 1000\)，询问次数 \(2.85 \times 10^4\)。

发现传统排序都没啥前途，考虑更暴力一点但是更容易拓展的做法：插入排序。直接插入排序当然也不好，但是我们可以插入的时候进行二分，然后用一些方法维护出每次插入一个数的序列即可。不过正常二分可以直接排除掉一半，这里并做不到，怎么办？一种方法是每次比较多比较几次，这样足够多次当然是可以大概率确定大小关系的，但是这样实际上丢失掉了很多概率的信息。我们考虑一个更本质一些的二分，正常二分我们做的实际上是将当前可能的集合与某一个前缀或后缀取交，我们每一刻维护的是这个位置可不可能是答案。而这里牵扯到了概率，那么我们实际上可以维护这个位置有多大概率成为答案。具体来说，我们一开始认为所有位置成为答案的概率都是等价的，我们每次可以取概率约为一半的位置进行分割，如果返回左边更小则左半部分有 \(90\%\) 的概率确实更小，右半部分有 \(10\%\) 的概率更小，反之亦然。那么我们可以给左右都乘上这个概率，当然注意到直接这样乘是不满足概率的性质的，可以再除以所有概率的和来得到真正的概率。（实际上好像是条件概率和贝叶斯公式一类的，不过懒得想这么多直接感性理解了）那么我们一直进行这个操作，直到有一个位置成为答案的概率 \(> 1-\varepsilon\) 时即可停止。这样已经可以得到比较优秀的结果了，但是还是不够。我们可以尝试设小 \(\varepsilon\)，这样询问次数会少，但是会导致有大概率会出错。不过实际上即使设小了一点出错的位置也比较少，可以顺着扫一遍找到不对的位置，然后再重新插回去，这样可以通过。

好像得用数据结构维护上面的排序过程，所以时间复杂度应该是 \(\log^2\) 的，所以似乎比较炸裂，，

T3 可达点对

给定一个 \(n \times m\) 的黑白矩阵，满足黑色点形成一个四连通块，白色点形成一个四连通块。多次询问，每次给定一个矩形，问在这个矩形内，可以只通过同色点互相四连通的点对数。

\(n, m \le 1000, q \le 20000\)

赛时根本没看到所有黑色点和白色点连成一个连通块的条件，，，

由于两种颜色均形成整个连通块，我们可以找到这两个连通块的分解线，容易发现这个分界线一定形成一条回路。我们可以先找出这条回路。然后现在考虑这个回路与询问矩形的交点。如果没有交则完全包含，容易直接计算答案。否则注意到边界上的边数是 \(O(n + m)\) 的，划分出来的一个连通块一定包含至少一条边界上的边，那么实际上连通块数就只有 \(O(n + m)\) 个，\(O(q(n+m))\) 的复杂度可以接受，所以我们只需要快速找到所有连通块就行了。

可以发现连通块一定是边界和回路交替形成的，我们可以直接从每条边界上的边开始走，每次沿边界或者回路走到下一个交点上去，这样就找到了所有的连通块。我们可以将边界上的所有交点全部按照回路上的顺序排个序，这样就能很容易的找到沿回路走到的下一个交点是哪里了。剩下的问题就是求连通块大小，这其实就是在多边形的面积，直接叉积就能做了，对于回路上连续的一段来说可以前缀和差分一下求叉积。对于排序，值域是 \(O(n^2)\) 级别的，可以基数排序 \(O(n)\)，或者直接 sort 也能过。

杂题：懒得写了，存下题号先。

「PA 2024」Dzielniki 「PA 2024」Desant 3 「PA 2024」Kolorowy las 「PA 2024」Grupa permutacji

2024.7.5

模拟赛疑似有点太困难了！！！

T1 不写了，反正大概就是注意到转移矩阵 or 系数 or 之类的东西可以用两个整数 \(p, q\) 来表示，且操作是令 \((p, q) \to (q, p - q)\) 之类的东西，所以可以直接辗转相除来做，需要解方程来得到 \(p, q\)。打表找规律题，不太想写了。原题，多次询问 \(f(a, b, c)\)

T2 是 有色图 的超级加强版，\(n \le 140\)，有点炸裂，倒是确实没见过分拆数 mitm。

T3 看着有点太炸裂了，反正是大量分讨加调整等，过于困难了，摆。

jjdw 因为上午被抓颓加上昨天上午睡了一上午有前科被劝退了，流汗

T2 有色图2.6415

首先 原题做法 就不写了，咕。

总之现在是要对于所有 \(n\) 的分拆，设 \(i\) 出现了 \(c_i\) 次，求 \(\frac{n!}{\prod i^{c_i} \times c_i!} \times (\sum c_i \lfloor\frac{i}{2}\rfloor + \sum_i \sum_j c_i c_j \gcd(i, j))\)。

首先前面的 \(\prod\) 是容易拆贡献的，\(\sum c_i \lfloor \frac i2 \rfloor\) 也是好说的，现在问题在于后面这个两个 \(\sum\) 很难搞，所以必须得枚举分拆数，但是这个数据范围又没法直接枚举出所有的分拆。这时候就思考一些优化暴力的方法了，比如 meet in the middle。

思考一下这道题怎么 meet in the middle，我们要优化枚举分拆的过程，注意到大部分时间实际上都浪费到枚举较小的数，所以我们考虑设一个阈值 \(B\)，对于 \(> B\) 的数直接枚举分拆，对于 \(\le B\) 的部分单独拿出来做。但是由于两个 \(\sum\) 的限制，我们还是需要知道大于 \(B\) 的 \(c_i\) 的信息的，不过实际上我们并不需要知道所有 \(c_i\) 都等于什么，我们要统计的部分贡献是 \(\sum_{i \le B} \sum_{j > B} c_i c_j \gcd(i, j)\)，那么我们实际上只需要维护出 \(f_i = \sum_{j > i} c_j \gcd(i, j)\) 就可以计算贡献了，这样就由记录 \(n\) 个数转成只需要记录 \(B\) 个数，同时每个 \(f_i\) 不超过 \(Bn\)，实际上有用的状态也远小于 \((Bn)^B\)，所以这部分可以直接记忆化搜索一下。\(B\) 大概可以取到 \(8\) 左右比较优。这样就能通过了。

2024.7.6

T3 优先队列

有 \(1 \sim n\) 这 \(n\) 个数和一个小根堆，有一个长为 \(n+m\) 的操作序列，每次可以是加入一个数或者删除最小值。你可以决定加入哪个数。问有多少种不同的加入数的方案，使得删除的数的集合为 \(A\)。
\(m \le n \le 300, |A| = m\)

首先有个没啥脑子的做法，钦定一下删除的顺序那么就能得到每个数加入的时间区间了，但是直接这么做没啥用。

进一步考虑一下，注意到由于每次删除最小值，如果一个不在 \(A\) 内的数被加入了队列，且这个数小于某个没被删除的 \(A\) 内的数，那么在之后某一时刻一定会使得这个数先弹出，所以在任意时刻，队列中集合外的数一定都大于 \(A\) 中没有被删除的数的最大值。而这个最大值是递减的，所以实际上对于不在 \(A\) 中的数的限制是逐渐放松的，那么每一轮就可以任意加入一个大于 \(A\) 内未删除的最大值的数，所以我们可以仅记录 \(A\) 集合内哪些数没有被删就可以做了。

实际上注意到我们连 \(A\) 集合内没被删的集合都不关心，我们仅关心当前 \(A\) 集合没被删的数的最大值等于多少。但是如果我们仅记录最大值，在最大值被删除后，我们就不知道新的最大值是多少了。我们不在加入 \(A\) 集合内的数的时候钦定这个数是啥，而是在最大值被删除之后，再确定新的最大值是什么，以及之前删除的非最大值都是什么就行了，这样就只需要记录当前队列中有多少 \(A\) 内的数和没被删除的数的最大值就能转移了。具体转移摆了。

2024.7.7

T2 帮派斗争 (Pakencamp 2022 Day2 H)

还是挺有趣的

考虑一个模拟：这个过程相当于是对 \(b_i\) 建出了一棵笛卡尔树，然后每次把 \(\sum a_i\) 较大的一边作为当前点的值传上来，现在问题就是根处的点值。这是从下往上来做的，这显然是不好做的，并且实际上我们只关心最后答案所在的那一条根链，所以对树进行操作实际上是很浪费的。

考虑从上往下来做，那么实际上我们做的就是每次找到区间内 \(b_i\) 的最大值，然后将区间分成两半，留下 \(\sum a_i\) 较大的一边，然后再递归下去直到仅剩一个点。

显然这样单次是会被卡到 \(O(n)\) 的，所以需要用某种方法加速这个过程。考虑每次快速进行若干次操作，如果能在这些操作后将 \(\sum a_i\) 总和减少到原来的某个常数倍那么其实就可以在 \(O(\log (\sum a_i))\) 轮内结束了。注意到每次选择的都是较大的一半，令 \(S = \sum a_i\)，那么如果存在一半总和大于 \(\frac S2\)，那么接下来留下的一定是这一半。我们可以考虑一次性跳到最后一个总和大于 \(\frac S2\) 的区间，这等价于找到一个 \(b_i\) 的最小值最大，且总和大于 \(\frac S2\) 的极长区间，可以发现这样的区间一定是上述过程中会跳到的区间，因为这相当于是在找笛卡尔树上 \(a_i\) 和大于 \(\frac S2\)，且深度最深的点，而笛卡尔树上 \(a_i\) 和大于 \(\frac S2\) 的点一定都是在路径上的点。那么我们只需要快速找到这样的一个区间就行了。

注意到总和大于 \(\frac S2\) 的区间一定经过带权中点，于是我们可以找到这个中点，并从这里划分开。由于要求 \(b_i\) 最小值最大，我们可以二分一个最小值 \(V\)，找到最长的满足 \(b_i \ge V\) 的区间，然后看这个区间和是否大于 \(\frac S2\)，这样朴素实现就是 \(O(n \log^3)\) 的。考虑优化这个二分的过程，这个东西可以类似于元旦激光炮的做法，在左右两个线段树上同时进行二分，就可以把这个过程优化到 \(O(\log n)\) 了，复杂度 \(O(n \log^2 n)\)。

有个更简单的做法：上面我们要求缩减到 \(\frac S2\)，我们可以把这个限制放松一点，每次缩减到 \(\frac {2}{3} S\)。我们同样可以找到中间 \(\frac 13 S\) 的区间，这个区间一定会被包含，考虑每次最大值的位置，如果在左边则一定保留右半部分，如果在右边则一定保留左半部分，如果在中间则一定会使得剩下的区间小于 \(\frac 23 S\)，那么这样就很好维护了，只需要考虑中间区间的 \(b_i\) 最小值，那么比这个大的 \(b_i\) 都会被切割一遍，在左右找到被切割的端点就行了。

2024.7.9

纯纯无聊比赛，没啥可写的

2024.7.10

弃赛了，不太理解放这玩意题想表达啥。

posted @ 2024-05-25 14:21  APJifengc  阅读(1860)  评论(193)  编辑  收藏  举报