「解题报告」The 1st Universal Cup. Stage 4 Ukraine
大概按难度排序。比较简单的题没写。
B. Binary Arrays and Sliding Sums
给定两个整数 \(n, k\),对于一个长为 \(n\) 的 01 序列 \(a_i\) 来说,由序列 \(a_i\) 生成的序列 \(b_i\) 为 \(\sum_{i=0}^{k-1} a_{i+k}\)(令 \(a_{i+n} = a_i\)),问对于所有的长为 \(n\) 的 \(a_i\) 序列,可以生成多少不同的 \(b_i\) 序列。
多测,\(T \le 10^5, k \le n \le 10^6\)
考察 \(b_i\) 可以由 \(b_1\) 和 \(b_i\) 的差分序列唯一确定。我们先考察差分序列,不难发现差分序列就是 \(a_i\) 数组中由 \(a_{i+k} - a_i\) 生成的序列。我们将它分成 \(g=\gcd(n, k)\) 个环,那么我们可以将每个环分开来考虑。发现,如果整个环全都是 \(0\) 或 \(1\),此时差分序列等于全 \(0\),否则我们一定可以由差分序列唯一确定一个原序列。于是一个环的方案数实际上就是 \(2^{n/g}-1\)。
但是此时我们还需要确定首位。由于我们已经把 \(a_i\) 拆成了 \(g\) 个环,那么对于 \(b_1\) 来说,如果一个环不是完全相同,那么它的所有 \(a_i\) 已经固定了,对 \(b_1\) 的贡献也是固定的;否则,这个环完全相同,那么对 \(b_1\) 的贡献就是 \(\frac kg a_i\),注意到我们只关心全相同的环中的 1 的个数,那么对于一组固定的差分序列,我们可以考虑其有 \(w\) 个完全相同的环,那么其 \(b_1\) 就有 \((w+1)\) 种选择。
那么我们就容易列出答案式子了:
化简一下即可得到 \(O(\log n)\) 计算的式子,利用 \(\binom{n}{i} i = \binom{n-1}{i-1} n\) 和二项式定理即可。
from math import gcd
P = 998244353
T = int(input())
for t in range(T):
n, k = map(int, input().split())
g = gcd(n, k)
print((pow(pow(2, n // g, P) - 1, g, P) + g * pow(pow(2, n // g, P) - 1, g - 1, P)) % P)
C. Count Hamiltonian Cycles
给你一个长为 \(2n\) 的字符串,字符为 W 或 B,构建一张无向图图,当且仅当 \(s_i \ne s_j\) 时 \(i, j\) 间有边,边权为 \(|i - j|\)。问长度最短的哈密顿回路的数量,两个环不同当且仅当存在一条边在一个环中出现了而在另一个环中没有出现。
\(n \le 10^6\)
我觉得我见过这种套路不止几百遍了,怎么我还是不会做???
首先肯定找一个合理的下界,每一条边被经过的次数等于两倍的左边黑白差的数量,当然由于必须是一个环,所以不能等于 \(0\),与 \(1\) 取个 \(\max\)。发现可以得到一个环所有边都达到下界。
考虑怎么得到。处理环有个经典的做法,就是依次加入每个点,维护当前链的集合。我们考虑从左到右依次加点,由于每一条剩余的链都会造成贡献,我们肯定要尽可能多的合并链。考虑前面黑白差,如果黑白数量相同,发现此时只会有一条链,头尾颜色不同。如果黑色多,应该会得到差值条首尾均为黑色的链,白色同理。这可以归纳的证明,每次尽可能多合并即可。但是仔细考虑一下就会发现有点问题,因为如果一条链的长度为 \(1\),那么和它合并的方案数为 \(1\) 而不是 \(2\),因为此时它的两端是等价的。不过我们可以将环变成有向环来解决这个问题,最后答案除以 \(2\) 即可。这样长度为 \(1\) 的链也有两种连法了。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2000005, P = 998244353;
int T, n;
char s[MAXN];
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d%s", &n, s + 1);
int ans = 1;
int sum = 0;
for (int i = 1; i <= 2 * n; i++) {
if (sum == 0) { // WBWBWB
// only one choice
} else if (sum > 0) { // BWBWB BWBWBWB
if (s[i] == 'W') {
int c = max(sum, 2);
ans = 1ll * ans * c % P * (c - 1) % P;
}
} else { // WBWBWBW WBWBW
if (s[i] == 'B') {
int c = max(-sum, 2);
ans = 1ll * ans * c % P * (c - 1) % P;
}
}
if (s[i] == 'B') sum++;
else sum--;
}
ans = 1ll * ans * ((P + 1) / 2) % P;
ans = 1ll * ans * ((P + 1) / 2) % P; // 最后一步会多算贡献,因为最后需要闭环,只有一种方案,但是计算了两种
printf("%d\n", ans);
}
return 0;
}
G. Graph Problem With Small \(n\)
给定一张无向图,对于所有点对 \((i, j)\),求是否存在一条从 \(i\) 开始到 \(j\) 结束的哈密顿路径。
\(n \le 24\)
首先有显然的 \(O(2^n n^3)\) 的状压 DP,然后容易压位做到 \(O(2^n n^2)\)。
考虑怎么优化到 \(O(2^n n)\)。我们考虑将哈密顿路径从 \(1\) 点处断开,跑一遍 DP 求出 \(f_{S, i}\) 表示从 \(1\) 开始,经过点集为 \(S\),到 \(i\) 结束的路径是否存在,这样只用 DP 一次,复杂度 \(O(2^n n)\)。然后可以直接把全集划分成两部分来统计答案,即可做到 \(O(2^n n)\)。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 24;
int f[1 << MAXN];
int n, e[MAXN];
char s[MAXN];
int ans[MAXN];
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%s", s);
for (int j = 0; j < n; j++) if (s[j] == '1') e[i] |= 1 << j;
}
f[1] = 1;
for (int s = 1; s < (1 << n); s += 2) if (f[s]) {
for (int i = 0; i < n; i++) if (!(s >> i & 1) && (f[s] & e[i])) {
f[s | (1 << i)] |= 1 << i;
}
}
for (int s = 1; s < (1 << n); s += 2) {
int t = (1 << n) - s;
for (int i = 0; i < n; i++) if (f[s] >> i & 1) ans[i] |= f[t];
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) printf("%d", ans[i] >> j & 1);
printf("\n");
}
return 0;
}
J. Jewel of Data Structure Problems
对于一个排列,定义其权值为最长的子序列长度,使得这个子序列的逆序对数为奇数。若不存在这样的子序列则权值为 \(-1\)。给定长为 \(n\) 的排列 \(p\),\(q\) 次修改操作,每次交换排列的两个数,每次修改后输出当前排列的权值。
\(n, q \le 2 \times 10^5\)
首先有经典结论:交换两个数会使得排列逆序对数奇偶性改变。考虑每个数与这两个数形成的逆序对数即可。
那么首先我们可以算出整个排列的逆序对数的奇偶性,然后每次交换后奇偶性改变,可以直接得到一些询问的答案为 \(n\)。考虑当逆序对为偶数时权值等于什么。
可以猜一个结论:权值只能是 \(\{-1, n - 1, n - 2\}\) 中的一个。
首先如果整个排列就是 \(\{1, 2, \cdots, n\}\) 那么答案就是 \(-1\),否则一定存在相邻两个数使得 \(p_i > p_{i+1}\),分类讨论一下可以发现删除 \(p_i\),删除 \(p_{i+1}\) 和删除 \(p_i, p_{i+1}\) 三种方案中一定存在至少一种使得逆序对奇偶性改变,于是实际上我们最多删除两个数就可以使得逆序对奇偶性改变了。那么我们只需要知道能不能删除一个数使得逆序对数改变即可。
考虑一个数删除后逆序对数减少量 \(c_i\)。其等于 \([1, i)\) 中 \(> p_i\) 的数量与 \((i, n]\) 中 \(< p_i\) 的数量之和。当然可以分块或者树套树来暴力维护这个,但是实际上我们不用,因为我们只关心 \(c_i\) 的奇偶性,上面求的是左上与右下两个矩形内的点数,我们可以改成求左边与下面两个矩形内的点数,两者奇偶性相同,而后者就等于 \((i-1) + (p_i - 1)\),这是很好维护的,于是修改容易做到单次 \(O(1)\)。
实际上一开始求逆序对奇偶性也可以做到 \(O(n)\),由于每次交换后奇偶性改变,我们只需要知道把这个排列排好序的交换次数的奇偶性即可,排列排序的最少交换次数等于 \(n\) 减置换环数(每次排序一个置换环即可),于是我们可以 \(O(n)\) 求出逆序对奇偶性,复杂度可以做到 \(O(n + q)\)。直接树状数组求逆序对数也可以通过。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 200005;
int n, q;
int p[MAXN];
struct BinaryIndexTree {
int a[MAXN];
#define lowbit(x) (x & (-x))
void add(int d) {
while (d <= n) {
a[d] ^= 1;
d += lowbit(d);
}
}
int query(int d) {
int res = 0;
while (d) {
res ^= a[d];
d -= lowbit(d);
}
return res;
}
void clear() { memset(a, 0, sizeof a); }
} bit;
int a[MAXN], c;
int cc[2];
int main() {
scanf("%d%d", &n, &q);
for (int i = 1; i <= n; i++) scanf("%d", &p[i]);
for (int i = 1; i <= n; i++) {
c ^= ((i - 1) & 1) ^ bit.query(p[i]);
a[i] ^= ((i - 1) & 1) ^ bit.query(p[i]);
bit.add(p[i]);
}
bit.clear();
for (int i = n; i >= 1; i--) {
a[i] ^= bit.query(p[i]);
cc[a[i]]++;
bit.add(p[i]);
}
int match = 0;
for (int i = 1; i <= n; i++) match += p[i] == i;
auto calc = [&](int i) {
return (((i - 1) & 1) ^ (p[i] ^ 1)) & 1;
};
while (q--) {
int x, y; scanf("%d%d", &x, &y);
match -= p[x] == x;
match -= p[y] == y;
swap(p[x], p[y]);
match += p[x] == x;
match += p[y] == y;
cc[a[x]]--, cc[a[y]]--;
a[x] = calc(x), a[y] = calc(y);
cc[a[x]]++, cc[a[y]]++;
c ^= 1;
if (c == 1) printf("%d\n", n);
else {
if (match == n) printf("-1\n");
else {
if (cc[1]) printf("%d\n", n - 1);
else printf("%d\n", n - 2);
}
}
}
return 0;
}
L. Least Annoying Constructive Problem
给定一个点数为 \(n\) 的完全图,构造一个边的环排列,满足任意相邻 \(n-1\) 条边都能形成一棵生成树。
\(n \le 500\)
APIO 讲的题。
考虑按照 \(n\) 为奇数与偶数分开构造。对于两个问题,我们用两种经典构造来解决:
对于 \(n\) 为奇数,考虑直接构造 \(\frac{n - 1}{2}\) 棵生成树然后在两两之间过渡。构造为先折线构造出一个,然后再循环做 \(\frac{n-1}{2}\) 遍。先考虑这两种之间怎么过渡,发现先从上到下依次删除每条斜边,然后再从下往上依次删除每条横边即可。实际上我们可以把一棵树拆成两组平行线,那么我们的构造也就是循环依次插入每一组平行线。最后可能剩下一些边没法直接形成生成树,直接按照平行线再构造一组即可。
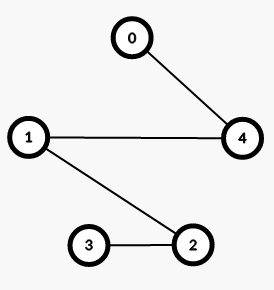
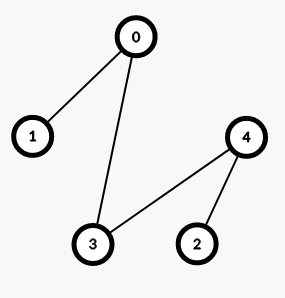
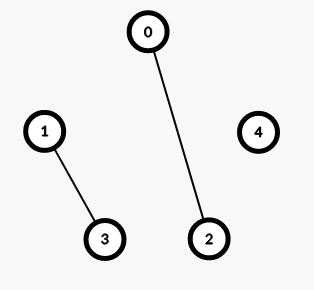
对于 \(n\) 为偶数,考虑构造 \(n-1\) 组匹配。构造方法是将一个点放在中间,然后每次选取一条中间向一个点的连边与所有和它垂直的边,然后循环构造一下。注意到相邻两组匹配之间也可以形成树,大概顺序是先加竖边然后再从下到上加每条横边。
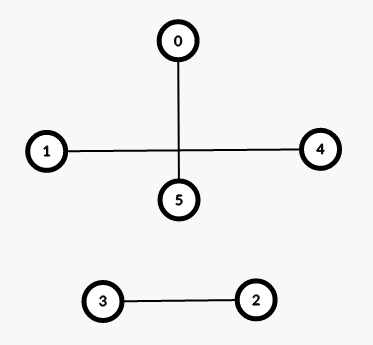
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 505;
int n;
void output(int u, int v) {
u++, v++;
if (u > v) swap(u, v);
printf("%d %d\n", u, v);
}
int main() {
scanf("%d", &n);
if (n & 1) {
for (int t = 0; t <= n / 2; t++) {
for (int i = 1; i <= n / 2; i++) output((i - 1 + t) % n, (n - i + t) % n);
if (t < n / 2) for (int i = n / 2; i >= 1; i--) output((i + t) % n, (n - i + t) % n);
}
} else {
for (int i = 0; i < n - 1; i++) {
output(n - 1, i);
for (int j = n / 2 - 1; j >= 1; j--) output((j + i) % (n - 1), (n - 1 - j + i) % (n - 1));
}
}
return 0;
}

