「解题报告」The 1st Universal Cup. Stage 5: Osijek
大概按难度排序。比较简单的题没写。
D. Distinct Subsequences
给定一个 \(01\) 串 \(s\),问 \(s\) 有多少长度为 \(k\) 的本质不同子序列。
\(k \le |s| \le 2 \times 10^5\)
首先本质不同子序列有经典 DP:设 \(lst_i\) 表示上一个与 \(s_i\) 相同的位置,那么有 \(f_i = \sum_{j=lst_i}^{i-1} f_j\),即如果上一个数字选在 \(lst_i\) 之前,那么下一个选择的位置应该是 \(lst_i\) 而不是 \(i\)。然后前缀和一下即可得到 \(g_i = g_{i-1} + g_{i-1} - g_{lst_i - 1}\)。
考虑加一维表示当前选择了多少数,那么就是 \(g_{i, j} = g_{i - 1, j} + g_{i - 1, j - 1} - g_{lst_i - 1, j - 1}\)。我们要求的就是 \(g_{n, k}\)。
这个东西看起来并不好优化转移,所以考虑写成多项式,即 \(G_i(x) = (1+x) G_{i-1}(x) - x G_{lst_i - 1}(x)\)。但是这里涉及到 \(lst_i - 1\),用到的多项式看起来跨度很大。不过注意到值域为 \(2\),那么我们可以直接存上一个 \(0\) 与上一个 \(1\) 的位置的多项式是什么,设 \(pre_{i, 0/1}\) 表示 \([1, i]\) 中最后一次 \(0/1\) 的出现位置,那么 \(lst_i = pre_{i - 1, s_i}\)。我们考虑将三个转移中需要用到的量 \(G_{pre_{i, 0}}, G_{pre_{i, 1}}, G_i\) 看作一个横向量,然后用矩阵刻画转移,容易得到转移矩阵。那么只需要将这 \(n\) 个矩阵分治乘起来就行了。时间复杂度 \(O(3^2 n \log^2 n)\)。我实现好像很慢啊,跑了 5.5s,卡着线跑进去了(
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 300005, P = 998244353, G = 3;
int qpow(int a, int b) {
int ans = 1;
while (b) {
if (b & 1) ans = 1ll * ans * a % P;
a = 1ll * a * a % P;
b >>= 1;
}
return ans;
}
const int GI = qpow(G, P - 2);
int r[MAXN];
void calcRev(int limit) {
for (int i = 1; i < limit; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) * limit >> 1);
}
void ntt(vector<int> &a, int limit, bool rev) {
for (int i = 0; i < limit; i++) if (i < r[i]) swap(a[i], a[r[i]]);
for (int mid = 1; mid < limit; mid <<= 1) {
int step = qpow(rev ? GI : G, (P - 1) / (mid << 1));
for (int l = 0; l < limit; l += (mid << 1)) {
int w = 1;
for (int i = 0; i < mid; i++, w = 1ll * w * step % P) {
int x = a[l + i], y = 1ll * a[l + i + mid] * w % P;
a[l + i] = (x + y) % P, a[l + i + mid] = (x - y + P) % P;
}
}
}
if (rev) {
int inv = qpow(limit, P - 2);
for (int i = 0; i < limit; i++) a[i] = 1ll * a[i] * inv % P;
}
}
typedef array<array<vector<int>, 3>, 3> matrix;
int n, k;
char s[MAXN];
matrix solve(int l, int r) {
if (l == r) {
matrix ret;
if (s[l] == '1') {
ret[0][0] = { 1 }, ret[0][1] = { 0 }, ret[0][2] = { 0 },
ret[1][0] = { 0 }, ret[1][1] = { 0 }, ret[1][2] = { 0, P - 1 },
ret[2][0] = { 0 }, ret[2][1] = { 1 }, ret[2][2] = { 1, 1 };
} else {
ret[0][0] = { 0 }, ret[0][1] = { 0 }, ret[0][2] = { 0, P - 1 },
ret[1][0] = { 0 }, ret[1][1] = { 1 }, ret[1][2] = { 0 },
ret[2][0] = { 1 }, ret[2][1] = { 0 }, ret[2][2] = { 1, 1 };
}
return ret;
}
int mid = (l + r) >> 1;
matrix L = solve(l, mid), R = solve(mid + 1, r), ret;
int limit = 1;
while (limit <= (r - l + 1)) limit <<= 1;
calcRev(limit);
for (int i = 0; i < 3; i++) for (int j = 0; j < 3; j++) {
L[i][j].resize(limit), R[i][j].resize(limit), ret[i][j].resize(limit);
ntt(L[i][j], limit, false), ntt(R[i][j], limit, false);
}
for (int k = 0; k < 3; k++) for (int i = 0; i < 3; i++) for (int j = 0; j < 3; j++) {
for (int t = 0; t < limit; t++) ret[i][j][t] = (ret[i][j][t] + 1ll * L[i][k][t] * R[k][j][t]) % P;
}
for (int i = 0; i < 3; i++) for (int j = 0; j < 3; j++) {
ntt(ret[i][j], limit, true);
}
return ret;
}
int main() {
scanf("%d%d%s", &n, &k, s + 1);
auto ret = solve(1, n);
printf("%d\n", ret[2][2][k]);
return 0;
}
C. Cyclic Shifts
给定一个长度为 \(n\) 的排列,每次选择 \(k\) 个位置 \(1 \le x_1 < x_2 < \cdots < x_k \le n\),然后将这 \(k\) 个位置向右循环移位一次(即 \(x_1 \to x_2, x_2 \to x_3, \cdots, x_k \to x_1\)),这样进行一次操作的代价是 \(\frac 1k\)。你需要在总代价不超过 \(2\) 的情况下将这个排列排好序。
\(n \le 5000\)
考虑选 \(n-1\) 个位置会发生什么,发现等价于将没选的那个位置与前一个位置 swap,然后再整体向右循环移位一次。
只有这个操作没啥用,但是我们可以选择多个不相邻的位置不选,然后就可以同时 swap 多个位置了。而且注意到每次操作的代价不会超过 \(\frac 2n\)。
那么我们就可以 sort 了。我们考虑冒泡,不过每次尽可能多 swap,于是先 swap 所有奇数位置再 swap 所有偶数位置即可。可以证明 \(n\) 次以内就能排好序,这个排序方法是与 CF1558F Strange Sort 的做法相同的。然后我们进行 \(n\) 次就可以恰好转一圈转回来了,这样正好 \(2\) 的代价。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 5005;
int n, a[MAXN];
char s[MAXN];
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
printf("%d\n", n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) s[j] = '1';
for (int j = ((n - i) & 1); j < n; j += 2) {
if (j + 1 < n && a[j] > a[j + 1]) {
swap(a[j], a[j + 1]);
s[(i + j + 1) % n] = '0';
}
}
printf("%s\n", s);
}
return 0;
}
H. Holiday Regifting
给定一张 DAG,每个点有一个容量 \(c_i\)。每一时刻点 \(1\) 会得到一个礼物,如果一个点的礼物数到达了容量,那么就会将礼物清空,并给出边所有点增加一个礼物。问使得所有点全部没有礼物的最小时刻,或报告不存在全部没有礼物的时刻。
\(n \le 10^4, m \le 3 \times 10^3, c_i \le 10^5\)
考虑按照拓扑序依次加入每一个点,维护使得前 \(i\) 个点全为 \(0\) 的周期 \(ans\)。显然每一个前缀都是周期性的。同时,我们维护出当前最小周期的时候所有点上各有多少礼物,设这个值为 \(a_i\)。
考虑加入下一个点,一个周期会得到 \(a_i\) 个礼物,要想礼物全部没掉就需要 \(\frac{c_i}{\gcd(c_i, a_i)}\) 个周期。我们将答案乘上这个值,并且将所有点上的礼物乘以这个值,然后再依据题意模拟一遍,就能得到新的最小周期与剩下所有点上礼物的个数了。时间复杂度 \(O(nm)\)。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 10005, MAXM = 100005, P = 998244353;
int n, m;
vector<int> e[MAXN];
int c[MAXN];
long long a[MAXN];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &c[i]);
for (int i = 1; i <= m; i++) {
int u, v; scanf("%d%d", &u, &v);
e[u].push_back(v);
}
int ans = 1;
a[1] = 1;
for (int i = 1; i <= n; i++) {
int g = c[i] / __gcd(1ll * c[i], a[i]);
ans = 1ll * ans * g % P;
for (int j = i; j <= n; j++) a[j] *= g;
for (int j = i; j <= n; j++) {
for (int k : e[j]) a[k] += a[j] / c[j];
a[j] %= c[j];
}
}
printf("%d\n", ans);
return 0;
}
E. Epidemic Escape
平面上有 \(n\) 个圆,其圆心 \((x_i, y_i)\),多组询问给出一条射线与一个整数 \(k\),一个点从原点出发,沿射线方向运动,同时所有圆的半径从 \(0\) 开始增加,走过 \(t\) 距离时所有圆的半径为 \(t\),问最早的时刻使得这个点被至少 \(k\) 个圆所覆盖。
\(n \le 10^5, k \le 5, |x_i|, |y_i| \le 10^9\),精度误差不超过 \(10^{-6}\)。
首先转换一下改成以当前点为圆心做经过原点的圆,然后问最早什么时候覆盖至少 \(k\) 个点。发现圆每时刻一定覆盖之前时刻的圆,所以可以直接考虑前 \(k\) 个到圆上的点。
考虑什么时候一个点会到圆上,简单几何知识可以得到,把所有点放到极坐标上,如果一个点为 \((r, \alpha)\),射线转向角为 \(\theta\),那么时刻就是 \(\frac{r}{2 \cos(\alpha - \theta)}\)。
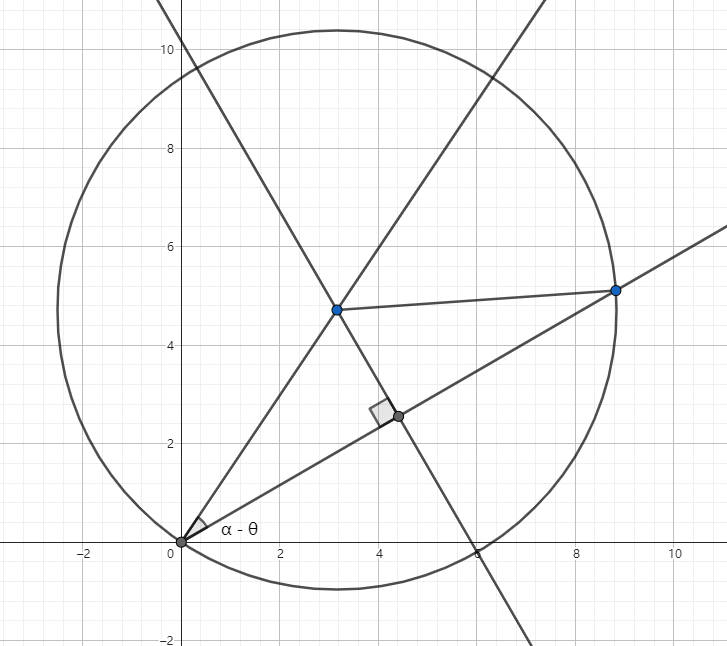
我们要找的就是 \(\frac{r}{2 \cos(\alpha - \theta)}\) 中 \(> 0\) 的第 \(k\) 小值,考虑取倒数,那么就是求 \(\frac{2 \cos(\alpha - \theta )}{r}\) 的前 \(k\) 大值了。拆一下上面的 \(\cos\),得到 \(\frac{2\cos\alpha}{r} \cos\theta + \frac{2\sin \alpha}{r} \sin \theta\),最大化它就相当于最大化 \((\frac{2 \cos \alpha}{r}, \frac{2 \sin \alpha}{r}) \cdot (\cos \theta, \sin \theta)\),容易发现这相当于用一条垂直于 \((\cos \theta, \sin \theta)\) 的斜线去切所有的点中第一个切到的点,那么我们可以维护出来所有 \((\frac{2 \cos \alpha}{r}, \frac{2 \sin \alpha}{r})\) 的点的凸包即可求最大值。求 \(k\) 大值我们可以暴力建 \(k\) 层凸包,一层建完之后把凸包上的点删掉再建下一层,这样每次查询找每层凸包里的最大值位置相邻 \(k\) 个点,这样 \(O(k^2)\) 个点中找第 \(k\) 大即可。注意 eps 需要开的很小,因为值域是 \(10^{-9}\) 级别的。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100005;
const long double eps = 1e-30;
int n, q, x[MAXN], y[MAXN];
pair<long double, long double> pt[MAXN];
bool vis[MAXN];
struct Convex {
int stk1[MAXN], top1;
int stk2[MAXN], top2;
long double cross(int i, int j, int k) {
return (pt[j].first - pt[i].first) * (pt[k].second - pt[i].second)
- (pt[k].first - pt[i].first) * (pt[j].second - pt[i].second);
}
void build() {
for (int i = 1; i <= n; i++) if (!vis[i]) {
while (top1 > 1 && cross(stk1[top1 - 1], stk1[top1], i) >= -eps) top1--;
stk1[++top1] = i;
}
for (int i = 1; i <= n; i++) if (!vis[i]) {
while (top2 > 2 && cross(stk2[top2 - 1], stk2[top2], i) <= eps) top2--;
stk2[++top2] = i;
}
for (int i = 1; i <= top1; i++) vis[stk1[i]] = 1;
for (int i = 1; i <= top2; i++) vis[stk2[i]] = 1;
}
vector<int> query(long double cos, long double sin) {
if (!top1) return {};
vector<int> ret;
for (int i = 1; i <= min(5, top1); i++) ret.push_back(stk1[i]);
for (int i = 1; i <= min(5, top2); i++) ret.push_back(stk2[i]);
for (int i = max(1, top1 - 4); i <= top1; i++) ret.push_back(stk1[i]);
for (int i = max(1, top2 - 4); i <= top2; i++) ret.push_back(stk2[i]);
if (sin >= 0) {
int l = 1, r = top1;
while (l < r - 2) {
int mid1 = (l + r) >> 1, mid2 = mid1 + 1;
if (pt[stk1[mid1]].first * cos + pt[stk1[mid1]].second * sin
< pt[stk1[mid2]].first * cos + pt[stk1[mid2]].second * sin) {
l = mid1;
} else {
r = mid2;
}
}
for (int i = max(1, l - 4); i <= min(r + 4, top1); i++) ret.push_back(stk1[i]);
} else {
int l = 1, r = top2;
while (l < r - 2) {
int mid1 = (l + r) >> 1, mid2 = mid1 + 1;
if (pt[stk2[mid1]].first * cos + pt[stk2[mid1]].second * sin
< pt[stk2[mid2]].first * cos + pt[stk2[mid2]].second * sin) {
l = mid1;
} else {
r = mid2;
}
}
for (int i = max(1, l - 4); i <= min(r + 4, top2); i++) ret.push_back(stk2[i]);
}
sort(ret.begin(), ret.end());
ret.erase(unique(ret.begin(), ret.end()), ret.end());
return ret;
}
} convex[6];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d%d", &x[i], &y[i]);
long long p = 1ll * x[i] * x[i] + 1ll * y[i] * y[i];
pt[i] = { 2.0l * x[i] / p, 2.0l * y[i] / p };
}
sort(pt + 1, pt + 1 + n);
for (int i = 1; i <= 5; i++) convex[i].build();
scanf("%d", &q);
while (q--) {
int x, y, k; scanf("%d%d%d", &x, &y, &k);
if (x == 0 && y == 0) {
printf("-1\n");
continue;
}
long double d = sqrtl(1ll * x * x + 1ll * y * y);
long double c = x / d, s = y / d;
vector<int> p;
for (int i = 1; i <= 5; i++) {
for (int j : convex[i].query(c, s)) p.push_back(j);
}
sort(p.begin(), p.end());
p.erase(unique(p.begin(), p.end()), p.end());
vector<long double> ans;
for (int i : p) ans.push_back(c * pt[i].first + s * pt[i].second);
sort(ans.begin(), ans.end(), greater<>());
if (ans.size() < k || ans[k - 1] < eps) printf("-1\n");
else printf("%.12Lf\n", 1 / ans[k - 1]);
}
return 0;
}
B. Balanced Permutations
对于一个长度为 \(n\) 的排列 \(p\),定义其权值为区间 \([l, r]\) 的个数,满足区间内最大值位于区间的两端,即 \(a_l\) 或 \(a_r\) 等于 \(\max_{i=l}^r a_i\)。
定义一个排列 \(p\) 是平衡的,当且仅当其在所有长为 \(n\) 的排列中权值最小。
给定 \(n, k, l\),求出字典序第 \(k\) 小的平衡排列与字典序第 \(l\) 大的平衡排列。
\(n \le 10^6, k, l \le 10^{18}\)
先考虑权值怎么计算。考虑最值分治,每次找到区间内最大值的位置,考虑区间内最大值等于它的区间。发现恰好有区间长度哥子区间满足最大值在端点处,剩下的不经过最大值的区间可以递归下去计算。那么发现,答案就是将排列按照最大值建成一棵线段树,所有区间的和。那么显然这个权值最小值应该是 \(O(n \log n)\) 级别的,每次分界点应该尽可能在中间是最优的,尽可能让最后递归的深度最小。
那么不难想到,合法的分界点应该就是某个区间内的任意一个点,因为我们只需要满足左右两个子树最小递归深度均不会很大即可。容易二分找到这个区间,把这个区间用一个数组 \(t_{len}\) 表示,合法区间为 \([l + t_{len}, r - t_{len}]\)。那么一个排列为平衡的充要条件就是,每次找到最大值,然后最大值在 \([l + t_{len}, r -t_{len}]\),且左右两个区间均为平衡排列。
考虑如何找到字典序第 \(k\) 小与第 \(l\) 大。注意到 \(n\) 很大的时候,平衡排列的个数远大于 \(k, l\),我们可以考虑先贪心找到字典序最小与最大的排列,然后只在最后一段较小的区域内找字典序第 \(k\) 小或第 \(l\) 大即可。
估算一下,大概在区间长度 \(25\) 多的时候区间内方案数超过 \(10^{18}\),那么我们可以先一直贪心填,然后当区间长度小于等于 \(50\) 时我们就可以用一些 \(O(\mathrm{poly}(n))\) 复杂度的 DP 来做。贪心找字典序最小和最大肯定是将较大的值 / 较小的值往左区间填,但是分界点并不好找,可以写出 \(n \le 50\) 的部分后打表找一下规律,发现字典序最大就是让分界点尽可能往左,字典序最小也是尽可能往左,但是当 \(t_{len} = t_{len-1}\) 时需要向右移动一格。这部分应当是可以归纳证明的,我也没仔细证就咕咕了。
那么现在就是要解决 \(n \le 50\) 的问题。考虑按位贪心,然后 DP 求出固定一个前缀后的方案数。我们考虑这样去做:从大到小依次考虑每一个数,如果当前这个数已经在确定的前缀中出现,那么就判定左区间合不合法,并向右区间递归;否则,就枚举这个数放在当前区间内的哪个位置,必须满足在 \([l + t_{len}, r - t_{len}]\) 内。然后我们向左递归,或者我们可以选择这个数不在当前区间内放,而是在其它区间内放。我们可以同时再维护出其它完整区间有多少数还没有填,我们先预处理出 \(g_n\) 表示长度为 \(n\) 的区间的稳定排列数,然后 DP 的过程中,向左区间递归时先将右区间的方案乘上,在之后的递归中可能往当前右区间放,也有可能在比当前区间更靠右的区间放,此时我们用组合数将右区间与之前的未确定的位置混合起来,这样就提前把数分配好了,之后就不需要考虑数放在哪个区间内了。
具体的,设 \(f_{l, r, a, b, c}\) 表示将区间 \([l, r]\) 内填入值域为 \([a, b]\) 的数,且区间外未确定的数的个数为 \(c\) 的方案数,那么如果 \(b\) 存在且合法,则转移 \(f_{pos_b + 1, r, a, b - 1, c}\),若 \(pos_b\) 不在区间内则直接转移 \(f_{l, r, a, b - 1, c}\),否则枚举分界点 \(t\),转移 \(f_{l, t - 1, a, b - 1, c + r - t} \times g_{r - t} \times \binom{c+r-t}{c}\),或者将 \(b\) 填到区间外没填的位置上,即 \(f_{l, r, a, b - 1, c - 1}\)。注意到 \(a\) 永远不变,且对每个 \((l, r, b)\) 来说 \(c\) 是固定的,所以这个 DP 是 \(O(n^4)\) 的,加上按位贪心的过程就是 \(O(n^6)\),但是转移点本来就比 \(n\) 少的多,状态很不满,而且常数很小,\(n\) 可能也不大,最后只跑了 18ms。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100005, MAXB = 52, B = 50;
const long long inf = LLONG_MAX / 2;
struct Number {
long long val;
Number(long long x = 0) : val(x) {}
operator long long() { return val; }
Number operator+(Number x) { return min(inf, val + x.val); }
Number operator*(Number x) {
__int128_t v = ((__int128_t) val) * x.val;
if (v <= inf) return v;
return inf;
}
void operator+=(Number x) { val = min(inf, val + x.val); }
};
int n;
long long k1, k2;
long long f[MAXN];
Number g[MAXN];
int t[MAXN];
Number C[MAXB][MAXB];
namespace Small {
int ans[MAXN];
void ss(int l, int r, int a, int b) {
if (l > r) return;
int len = r - l + 1;
int mid = l + t[len], vmid = a + t[len];
if (len > 1 && t[len] == t[len - 1]) mid++, vmid++;
ss(l, mid - 1, a, vmid - 1), ss(mid + 1, r, vmid, b - 1);
ans[mid] = b;
}
bool used[MAXN];
int pos[MAXN];
Number f[MAXB][MAXB][MAXB];
bool vis[MAXB][MAXB][MAXB];
int L;
int checked[MAXB][MAXB];
bool check(int l, int r) {
if (l > r) return true;
if (checked[l - L][r - L]) return checked[l - L][r - L] - 1;
int x = 0;
for (int i = l; i <= r; i++) if (!x || ans[i] > ans[x]) x = i;
int len = r - l + 1;
if (x < l + t[len] || x > r - t[len]) checked[l - L][r - L] = 1;
else checked[l - L][r - L] = 1 + (check(l, x - 1) && check(x + 1, r));
return checked[l - L][r - L] - 1;
}
Number calc(int l, int r, int a, int b, int c) {
if (c < 0) return 0;
if (l > r) return 1;
if (a > b) return 0;
if (vis[l - L][r - L][b - a]) return f[l - L][r - L][b - a];
vis[l - L][r - L][b - a] = 1, f[l - L][r - L][b - a] = 0;
auto &ret = f[l - L][r - L][b - a];
int len = r - l + 1;
if (!used[b]) {
ret += calc(l, r, a, b - 1, c - 1);
for (int i = l + t[len]; i <= r - t[len]; i++) if (!ans[i]) {
ret += calc(l, i - 1, a, b - 1, c + r - i) * g[r - i] * C[c + r - i][c];
}
} else {
if (pos[b] < l) ret += calc(l, r, a, b - 1, c);
else if (pos[b] >= l + t[len] && pos[b] <= r - t[len] && check(l, pos[b] - 1))
ret += calc(pos[b] + 1, r, a, b - 1, c);
}
return ret;
}
void dfs(int l, int r, int a, int b) {
int len = r - l + 1;
if (len <= B) {
for (int i = l; i <= r; i++) {
for (int j = a; j <= b; j++) if (!used[j]) {
ans[i] = j;
pos[j] = i;
used[j] = 1;
L = l;
memset(vis, 0, sizeof vis);
memset(checked, 0, sizeof checked);
Number w = calc(l, r, a, b, 0);
if (w < k1) {
k1 -= w;
used[j] = 0;
pos[j] = 0;
} else {
break;
}
}
}
} else {
int mid = l + t[len], vmid = a + t[len];
if (len > 1 && t[len] == t[len - 1]) mid++, vmid++;
ss(l, mid - 1, a, vmid - 1);
ans[mid] = b;
dfs(mid + 1, r, vmid, b - 1);
}
}
void solve() {
if (n <= B && k1 > g[n]) printf("-1\n");
else {
dfs(1, n, 1, n);
for (int i = 1; i <= n; i++) printf("%d ", ans[i]); printf("\n");
}
}
}
namespace Bigger {
int ans[MAXN];
void ss(int l, int r, int a, int b) {
if (l > r) return;
int len = r - l + 1;
int mid = l + t[len], vmid = b - t[len];
ss(l, mid - 1, vmid, b - 1), ss(mid + 1, r, a, vmid - 1);
ans[mid] = b;
}
bool used[MAXN];
int pos[MAXN];
Number f[MAXB][MAXB][MAXB];
bool vis[MAXB][MAXB][MAXB];
int L;
int checked[MAXB][MAXB];
bool check(int l, int r) {
if (l > r) return true;
if (checked[l - L][r - L]) return checked[l - L][r - L] - 1;
int x = 0;
for (int i = l; i <= r; i++) if (!x || ans[i] > ans[x]) x = i;
int len = r - l + 1;
if (x < l + t[len] || x > r - t[len]) checked[l - L][r - L] = 1;
else checked[l - L][r - L] = 1 + (check(l, x - 1) && check(x + 1, r));
return checked[l - L][r - L] - 1;
}
Number calc(int l, int r, int a, int b, int c) {
if (c < 0) return 0;
if (l > r) return 1;
if (a > b) return 0;
if (vis[l - L][r - L][b - a]) return f[l - L][r - L][b - a];
vis[l - L][r - L][b - a] = 1, f[l - L][r - L][b - a] = 0;
auto &ret = f[l - L][r - L][b - a];
int len = r - l + 1;
if (!used[b]) {
ret += calc(l, r, a, b - 1, c - 1);
for (int i = l + t[len]; i <= r - t[len]; i++) if (!ans[i]) {
ret += calc(l, i - 1, a, b - 1, c + r - i) * g[r - i] * C[c + r - i][c];
}
} else {
if (pos[b] < l) ret += calc(l, r, a, b - 1, c);
else if (pos[b] >= l + t[len] && pos[b] <= r - t[len] && check(l, pos[b] - 1))
ret += calc(pos[b] + 1, r, a, b - 1, c);
}
return ret;
}
void dfs(int l, int r, int a, int b) {
int len = r - l + 1;
if (len <= B) {
for (int i = l; i <= r; i++) {
for (int j = b; j >= a; j--) if (!used[j]) {
ans[i] = j;
pos[j] = i;
used[j] = 1;
L = l;
memset(vis, 0, sizeof vis);
memset(checked, 0, sizeof checked);
Number w = calc(l, r, a, b, 0);
if (w < k2) {
k2 -= w;
used[j] = 0;
pos[j] = 0;
} else {
break;
}
}
}
} else {
int mid = l + t[len], vmid = b - t[len];
ss(l, mid - 1, vmid, b - 1);
ans[mid] = b;
dfs(mid + 1, r, a, vmid - 1);
}
}
void solve() {
if (n <= B && k2 > g[n]) printf("-1\n");
else {
dfs(1, n, 1, n);
for (int i = 1; i <= n; i++) printf("%d ", ans[i]); printf("\n");
}
}
}
int main() {
scanf("%d%lld%lld", &n, &k1, &k2);
C[0][0] = 1;
g[0] = 1;
for (int i = 1; i <= n; i++) {
f[i] = i + f[(i - 1) >> 1] + f[i >> 1];
int l = 0, r = (i - 1) >> 1;
while (l < r) {
int mid = (l + r) >> 1;
if (i + f[mid] + f[i - mid - 1] == f[i]) r = mid;
else l = mid + 1;
}
t[i] = l;
if (i <= B) {
C[i][0] = 1;
for (int j = 1; j <= i; j++) C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
for (int j = 1 + t[i]; j <= i - t[i]; j++) {
g[i] += C[i - 1][j - 1] * g[j - 1] * g[i - j];
}
}
}
Small::solve();
Bigger::solve();
return 0;
}

