2024.1 训练纪要

合集 - 做题纪要(13)

1.2023.9 做题纪要 #12023-08-31 2.2023.9 做题纪要 #22023-09-15 3.2023.10 做题纪要 #12023-10-03 4.2023.10 做题纪要 #22023-10-16 5.2023.10 做题纪要 #32023-10-25 6.2023.11 做题纪要 #12023-11-06 7.2023.12 做题纪要 #12023-12-11 8.2023.12 做题纪要 #22023-12-19

9.2024.1 训练纪要2024-01-01

10.2024.2 训练纪要2024-02-15 11.2024.3 做题纪要2024-03-19 12.2024.4 做题纪要2024-04-07 13.NOI 2024 前做题纪要2024-05-25

nfls 线上训练。

其实没想好这篇博要怎么写。大概就还是写个 solution set 之类的吧。

这个要加入做题纪要合集吗？？

2024.1.1
- R17 T2 Beautiful World (SDWC2021 Day3T3 美丽的世界)
2024.1.2
- R18 T1 掉落 (CF780G Andryusha and Nervous Barriers)
- R18 T2 原神 (湖南集训树上的棋局)
- R18 T3 区间mex快速算法 (2021 集训队互测 Round 10 T3 染色)
2024.1.3
- L1.3 T1 Kevin and Grid (CF1392I)
- L1.3 T2 prefix sum
- L1.3 T3 飞翔的胖鸟
- L1.3 T4 Beautiful Matrix (CF1085G)
2024.1.4
- L1.3 T5 分层图
- L1.3 T6 复读机加强版
- L1.3 T7 愚蠢的在线法官 (2021 集训队互测 Round 1 T1)
2024.1.5
- R19 T3 树与
- L1.3 T8 抽奖机
2024.1.6
- R20 T2 原神账号
- R20 T3 肖芬途
- ABC335G Discrete Logarithm Problems
2024.1.7
- CF1919F2 Wine Factory
- Gym103371I Organizing Colored Sheets
- QOJ1884 Mission Impossible: Grand Theft Auto
2024.1.8
- R21 T1 盗梦空间
- R21 T2 偷藏女装 (ARC068F Solitaire)
- R21 T3 楼梯调度
2024.1.9
- R22 T1 染色问题
- R22 T2 IOer
- R22 T3 力脑
2024.1.10
- L1.3 T? 好像是个 FWT 题
- L1.10 T1 (P5829【模板】失配树)
- L1.10 T2 (P4156 [WC2016] 论战捆竹竿)
- L1.10 T3 (P4548 [CTSC2006] 歌唱王国)
- L1.10 T4 (HDU6791 Tokitsukaze, CSL and Palindrome Game)
2024.1.11
- L1.10 T5 (ROI 2016 DAY2 二指禅)
- L1.10 T6 (CF1483F Exam)
2024.1.12
- R23 T1 星际逃亡
- R23 T2 博弈问题
2024.1.13
2024.1.15
- R25 T3 Dark Blue (GYM102803E)
2024.1.16
- L1.10 T8 (CF1276F Asterisk Substrings)
2024.1.17
- L1.17 T1 (Gym102538H Horrible Cycles)
- L1.17 T2 (AT_hitachi2020_f Preserve Diameter)
2024.1.18
- L1.17 T4 (CF1450H2 Multithreading (Hard Version))
- P3236 [HNOI2014] 画框
2024.1.19
2024.1.20
- R28 T3 deadline
2024.1.21
2024.1.22
- R29 T3 哈夫曼回路
- CF1375G Tree Modification
2024.1.23
- R30 T3 点点的圈圈
- CF103E Buying Sets

2024.1.1

100 / 10 / 15, sum 125, rank 10/35

怎么我这次来打的第一场又是没啥人打导致排名靠前，历史总是惊人的相似。

但是打的还是彩笔，T2 读错题想了半天，开始写暴力了才意识到读错题了 /cf

T3 似乎不太可改

R17 T2 Beautiful World (SDWC2021 Day3T3 美丽的世界)

考虑建图，然后显然一个连通块内要选边数个点，那么只有树与基环树是合法的，那么我们直接考虑两种情况。基环树显然是只有 2 种选择，树可以从每个点开始，有 $n$ 种选择，总之两者均可以处理出来若干个二元组 $(l, r)$ 表示左部点权值加 $l$ ，右部点权值加 $r$ 。那么现在问题就是，从若干个这样的二元组集合中每个集合选出一个，使得 $(\sum l) (\sum r)$ 最小。

我们考虑将这样的二元组画到平面上。注意到权值相等的点在一条反比例函数的曲线上，这个图像是凸的，也就是说任意两点之间的边上的点的权值一定是比两个端点大的，那么也就是说将这些点求出一个凸包来，实际上只有左下凸包上的点可能成为最小值。那么我们实际上只需要最后将所有的点合并成一个点集后，这个点集的凸包上的点即可。而注意到合并过程就是两个点集的闵可夫斯基和，于是我们只需要对集合的凸包做闵可夫斯基和即可。分治一下或启发式合并容易做到 $O (n \log n)$ 。

2024.1.2

100 / 68 / 25, sum 193, rk 21/56

果然马上就 20+ 了，哈哈！

不过似乎是很可打的一场，但是太久不写 ds 了代码能力确实下降，T1 调了半天 2h 才过，T2 好像挺典的，不过又没想到直径，我是 shaber。卡在了一个很尴尬的位置，如果 T2 或 T3 多打一档分就能进前十了，好像也没啥意义

草原来 T3 部分分这么简单，亏了。

R18 T1 掉落 (CF780G Andryusha and Nervous Barriers)

昨天 soy D 我为什么不写 T1，那我写下 T1。

发现多个球落到一个平台之后就没有任何区别了，所以我们只需要维护出每个平台上掉下来多少球，进而我们只需要知道从每个位置开始往下落能落到哪个平台上，一共有 $O (w + n)$ 个点需要计算。考察限制形如 $u_{i} < u_{j}, u_{i} + s_{i} \geq u_{j}, l_{j} - 1 / r_{j} + 1 \in [l_{i}, r_{i}]$ ，发现是个三维偏序，直接 CDQ 加线段树即可。复杂度 $O ((w + n) \log^{2} n)$ 。

R18 T2 原神 (湖南集训树上的棋局)

简要题意：给你一棵有根树，每个点上有一个棋子，每次可以将一个棋子移动到子树内除了当前节点外的任意一个节点， $q$ 次操作，每次将一条链上或一棵子树内的所有节点上加一个棋子和换根操作，询问当前局面的 SG 值。

题解：本来想把树剖卡掉只放全局平衡二叉树过的。要真这么干就鉴定为纯纯玩原神玩的。哦搬题人名字就是原神启动。

但是好像做法很典了，典到我甚至感觉我考过这个，没准我还真考过这个，也不好说。

首先容易根据 SG 一套理论把每个棋子分开，其中一个棋子的 SG 值是子树的最大深度，那么问题就是支持子树异或树链异或换根操作。

首先可以处理出距离每个点最远的距离和次远的距离，那么以任意一个点为根的时候只有可能是这两个值，而如果根在最远点所在子树内则 SG 是次远值，否则是最远值。而最远距离一定是树的直径的两个端点之一，那么我们将直径从中间分开，左边的点的最远点都是右端点，右边点的最远点都是左端点，对于某一个点为根时，所有的取到最远点的点就是根到直径中点上的所有点。

那么操作就简单了，换根操作就是将一条路径的最大与次大值翻转，修改是对存在与不存在翻转，那么我们线段树维护一个 $2 \times 2$ 的矩阵，然后操作就是上下翻转或者左右翻转，直接上线段树维护即可。

R18 T3 区间mex快速算法 (2021 集训队互测 Round 10 T3 染色)

考虑维护没有出现的数的集合，这样区间 mex 就是集合中的最小值。

假如 mex 固定，那么第三个操作可以使用线段树来维护，首先找出区间内的最小值，然后再将所有最小值的位置加 $c$ ，只需要维护一个对最小值的位置加 $c$ 的标记即可。

带修那么我们考虑大力在线段树上维护一下这个集合。首先我们将操作 12 变得更简单一些，我们对每个值维护一棵珂朵莉树，这样我们就只有区间覆盖与删除一个覆盖的区间的操作了，不需要判断原来是否存在。然后我们就可以上线段树了，每个线段树节点上维护一个可删堆，区间覆盖时则将区间内访问到的线段树的节点内插入这个值，那么一个点的集合就是这个点的叶子到根上的所有可删堆的并。删除时我们可以保证删除的区间与加入时的区间一模一样，这样只需要将插入时访问到的元素再删一遍即可，这只需要在珂朵莉树将一个区间分裂开时先把原区间删去，然后将两个新区间加入即可。我们在线段树上维护出最小值与最小值出现次数，再维护出最小值处加的标记，注意到我们这个过程中是不能将可删堆的内容下传的，所以当我们访问到需要修改的最小值所在的区间时，我们需要将最小值操作变成区间加操作，因为这下面的所有点的 mex 一定都是最小值。

2024.1.3

计数与数学专题。

L1.3 T1 Kevin and Grid (CF1392I)

~~以下你将看到震撼人心的符号语言~~。

首先网格图是平面图，我们有平面图欧拉定理：连通块数等于 $| V | - | E | + | F |$ 。 $V$ 与 $E$ 是容易刻画的，考虑 $F$ 的数量怎么求。对于网格图上来说， $F$ 分两种，一种是四个相邻的点之间的面，一种是若干空点形成的八连通块。注意到对于本题的网格来说，不可能出现斜角联通的情况，所以实际上还是空点形成的四联通块。那么注意到，这里的 $F$ 与另一张图的连通块数是关系很密切的。

我们先不考虑连通块是否在边上，我们先求出连通块数量。记 $a n s_{\geq x}$ 为 $\geq x$ 的点形成的连通块数， $a n s_{< x}$ 的点形成的连通块数。简单的想法是 $a n s_{\geq x} = c n t (o) - c n t (oo) - c n t (8) + c n t (88) + a n s_{< x}$ ，但是实际上这是错误的，因为并不是所有的 $< x$ 的连通块都是 $\geq x$ 的图中的面，因为有些连通块在边缘上，那么我们记 $s p e_{\geq x}$ 为 $\geq x$ 的点的边缘的连通块的数量， $< x$ 同理，那么答案就是 $a n s_{\geq x} = c n t (o) - c n t (oo) - c n t (8) + c n t (88) + a n s_{< x} - s p e_{< x}$ ，也就有 $a n s_{\geq x} - a n s_{< x} + s p e_{< x} = c n t (o) - c n t (oo) - c n t (8) + c n t (88)$ ，后面这个东西相对好计算的多，假设我们现在能求出 $a n s_{\geq x} - a n s_{< x} + s p e_{< x}$ ，同理我们能求出 $a n s_{< x} - a n s_{\geq x} + s p e_{\geq x}$ 。注意到我们要求的答案实际上是 $2 a n s_{\geq x} + s p e_{\geq x} - 2 a n s_{< x} - s p e_{\geq x}$ ，这就是上面两个值的差。

现在问题是怎么求出 $c n t$ ，这就是要求 $\sum_{i = 1}^{n} \sum_{j = 1}^{m} [a_{i} + b_{j} \geq x]$ ，由于值域很小，我们直接 NTT 就能求出每个 $a_{i} + b_{i}$ 出现了多少次，然后后缀和一下即可。边之类的也是一样的，我们只需要考虑最小值 $\geq x$ ，于是把相邻两个 $a_{i}$ 或 $b_{i}$ 的最小值加起来做就行了。然后因为我们不能取模，而答案是 $10^{10}$ 级别的，所以我们可以用两个模数跑 NTT 然后 CRT 合并起来就行了。

L1.3 T2 prefix sum

~~首先我们有暴力重构算法，直接每 $B = \sqrt{n k}$ 次重构一遍，每次查询把最后 $B$ 次修改操作的贡献加上即可。~~

二维前缀和有经典的用两个 BIT 维护 $a_{i}$ 与 $i \cdot a_{i}$ 的前缀和做法，那么 $k$ 维前缀和可以同样的方法去做，考虑一个 $a_{0, x}$ 对 $a_{k, y}$ 的贡献是 $(\binom{y - x + k - 1}{k - 1})$ ，那么查询的答案就是 $\sum_{i = 1}^{x} (\binom{x - i + k - 1}{k - 1}) a_{i}$ ，组合数是关于 $x$ 与 $i$ 的一个 $k$ 次多项式，可以暴力处理出来，然后查询的时候就只需要查询 $k$ 次 $i^{p} \cdot a_{i}$ 的前缀和即可。

L1.3 T3 飞翔的胖鸟

简要题意：求 $\frac{a h}{\sin θ} + b θ, θ \in (0, \frac{π}{2}]$ 的最小值。

直接求导，极值点满足 $b - \frac{a h \cos θ}{\sin^{2} θ} = 0$ ，即 $b (1 - \cos^{2} θ) = a h \cos θ$ ，这是一个关于 $\cos θ$ 的二次方程，直接解出来然后反三角函数即可。注意 $b = 0$ 时退化成一次方程。

L1.3 T4 Beautiful Matrix (CF1085G)

这题写起来是真的难受，细节非常诡异。

考虑枚举第一行不相同的是哪行。如果是第一行，发现只需要找到第一行的排列的排名即可，直接康托展开，下面每一行都是一个错排。

如果不是第一行，下面的行仍然是错排，重点在于这一行必须与上一行形成错排，所以相当于要求一个错排的排名。

仍然枚举第 $(i, j)$ 个数是第一个不同的数，这样前 $j - 1$ 个数确定了。假设枚举了 $(i, j)$ 是啥，那么对于后 $n - j$ 个数，有一些位置需要和上一行的数不相同，而有一些位置上一行的数已经出现过了，这一位相当于能任意填，那么这相当于有若干个位置需要错排，若干个位置没有限制。我们设 $f_{i, j}$ 表示 $i$ 个数中 $j$ 个数需要错排的方案数，那么就可以计算方案数了。注意到第 $(i, j)$ 个数只会使得后面的限制变化 $1$ ，所以我们可以维护出选哪些数使得限制数为 $x$ ，哪些数为 $x + 1$ 。然后只需要选 $< a_{i, j}$ 的数即可，用 BIT 维护。

考虑 $f_{i, j}$ 怎么求，当 $i = j$ 时就是错排，否则考虑将一个无限制的位置填一个数，如果填到 $j$ 内一个数那么这个数就没有限制了，否则仍然有限制，所以 $f_{i, j} = j f_{i - 1, j - 1} + (i - j) f_{i - 1, j}$ 。

2024.1.4

计数与数学专题 Day2。

下午和晚上将 jjdw 的诡异题代码整了出来，并迭代了三版，现在初版做法已经被爆踩了。做法极其抽象，但是题面居然显得很正常，非常神秘。希望不会再被评个 4.5 分。

L1.3 T5 分层图

简要题意：给定 $l \times n$ 个节点的图，分成 $l$ 层，每层是 $n$ 个点的完全图，相邻两层之间的 $n$ 对点对应连边。求这张图的哈密顿回路数量。 $n \leq 500, l \leq 10000$ 。

考虑类似于插头 DP 的做法，我们从某一块划分开，则上面分成了若干条链，每一条链的长度至少为 $2$ ，且两个插头有顺序（环的方向）。每次向下转移一层，我们将这些插头与剩下的孤立点进行连接，得到新的若干段，最后一层时将所有段全部连接起来就是答案。

那么我们设计 DP，只用记录当前有多少段。假设上一层有 $i$ 段，那么有 $2 i$ 个插头，剩下 $n - 2 i$ 个孤立点，如果把这些孤立点也看作一段那么一共就是 $n - i$ 段，我们需要将 $n - i$ 段划分成 $j$ 部分，每一部分依次连接起来。划分的方案数是 $\frac{(n - i)!}{j!} (\binom{n - i - 1}{j - 1})$ ，就是先把所有段排列，然后再分，最后分成的每一段之间没有顺序。直接 EGF 也可以推得这个式子。但是注意到这样有可能会使孤立点分到单独的一段内，这是不合法的，所以需要容斥一步。这个转移系数是固定的，所以只需要 $O (n^{3})$ 一遍处理出来即可。

然后矩阵快速幂一下。注意到段数是 $\frac{n}{2}$ 的，所以 $O (n^{3} \log l)$ 可以接受。最后一层计算答案的时候就是将 $n - i$ 段环排列，乘 $(n - i - 1)!$ 统计答案即可。

L1.3 T6 复读机加强版

首先单位根反演可以得到答案等于 $[\frac{x^{n}}{n!}] (\frac{1}{d} \sum_{i = 0}^{d - 1} e^{ω_{d}^{i} x})^{k}$ 。

$d = 1$ 时答案显然是 $k^{n}$ 。

$d = 2$ 时式子是 $(e^{x} + e^{- x})^{k}$ ，可以直接二项式定理展开，答案是 $\sum_{i = 0}^{k} (\binom{k}{i}) (2 i - k)^{n}$ 。

$d = 3$ 时由于 $k \leq 1000$ ，用上面的方法接着做就行了。

$d = 4$ 和 $d = 6$ 显然就不能这么整了。不过我们有一个有趣的性质： $d = 4$ 时 $ω_{4} = i$ ，即虚数单位，容易得知 $ω_{4}^{2} = - 1, ω_{4}^{3} = - i$ ，也就是说四种单位根可以用 $1, i$ 的线性组合表示出来。有结论：仅用 $φ (n)$ 个单位根 $ω_{n}^{i}$ 即可表示出所有 $ω_{n}^{k}$ 单位根。注意到 $φ (3) = φ (4) = φ (6) = 2$ ，也就是说这三种情况的单位根都可以用两个单位根来表示。 $d = 4$ 的情况上面已经明确了， $d = 6$ 时 $ω_{6}^{2} = ω_{6} - 1, ω_{6}^{3} = - 1, ω_{6}^{4} = - ω_{6}, ω_{6}^{5} = - ω_{6} + 1$ 。

那么也就是说，最后的 $e^{k x}$ 的指数系数一定是 $1, ω$ 的线性组合，即 $e^{(i + j ω) x}$ ，那么我们只需要知道每一对 $(i, j)$ 的出现次数，这样就能直接 $O (k^{2})$ 计算答案了。

而计算答案相当于计算 $[x^{i} y^{j}] (x + x^{- 1} + y + y^{- 1})^{k}$ 与 $[x^{i} y^{j}] (x + y + x^{- 1} y + x y^{- 1} + x^{- 1} + y^{- 1})^{k}$ 。首先可以乘一个 $x^{k} y^{k}$ 将负指数全部消掉，然后就是一个二元 GF 的幂，这可以大力 ODE 做到 $O (k^{2})$ 求出所有系数，然后就做完了。

L1.3 T7 愚蠢的在线法官 (2021 集训队互测 Round 1 T1)

我没看懂阿，把代码贺了。

官方题解和课件的做法都没看懂，我比较废物。

首先如果 $a_{i}$ 有相同的那答案一定等于 $0$ ，因为行列式有一行相同。

然后发现同时交换一行与一列行列式答案不变，所以可以把 $a_{i}$ 随便排序一下。

考虑每次从 lca 处合并两部分，假设第一部分的矩阵是 $A$ ，第二部分的矩阵是 $B$ ，那么两部分合并起来的矩阵应当形如：

[\begin{matrix} A & v_{u} \\ v_{u} & B \end{matrix}]

两部分自己的矩阵还是自己的矩阵，两部分之间的贡献全部都是当前的 lca 的权值 $v_{u}$ 。

然后考虑维护这个矩阵的行列式。考虑到全局矩阵减一个 $v_{u}$ 之后，行列式就等于左上与右下两个小矩阵的行列式的乘积了，所以考察这个怎么做。记 $A_{t}$ 为全局减去一个 $t$ 的矩阵，那么有：

\begin{aligned} det A_{t} & = \sum_{P} (- 1)^{c (p)} \prod_{i = 1}^{n} (A_{i, P_{i}} - t) \\ = \sum_{S \subseteq [1, n]} (- t)^{| S |} \sum_{P} (- 1)^{c (p)} \prod_{i \notin S} A_{i, P_{i}} \end{aligned}

注意到后面的式子如果 $| S | \geq 2$ 的话，我们可以找到两个数 $i \neq j \in S$ ，并交换 $P_{i}, P_{j}$ ，后面的 $\prod$ 肯定不变，而逆序对奇偶性变化，所以后面的式子一定等于 $0$ 。那么此时只需要考察 $| S | \leq 1$ 的情况，有：

det A_{t} = det A - t \sum_{j = 1}^{n} \sum_{P} (- 1)^{c (p)} \prod_{i \neq j} A_{i, P_{i}}

我们记 $\underset{s}{det} A = \sum_{j = 1}^{n} \sum_{P} (- 1)^{c (p)} \prod_{i \neq j} A_{i, P_{i}}$ ，那么有 $det A_{t} = det A - t \underset{s}{det} A$ 。我们只需要维护出每个矩阵的 $det A$ 与 $\underset{s}{det} A$ 即可。

实际上 $\underset{s}{det} A$ 相当于将 $A$ 的任意一行全部变成 $0$ 后的行列式之和，那么根据初等行变换， $\underset{s}{det} A = \underset{s}{det} A_{t}$ 。

那么考察怎么合并信息：

\begin{aligned} {det}_{s} [\begin{array}{c} A & v_{u} \\ v_{u} & B \end{array}] & = {det}_{s} [\begin{array}{c} A_{v_{u}} & 0 \\ 0 & B_{v_{u}} \end{array}] \\ = {det}_{s} A \times det B_{v_{u}} + det A_{v_{u}} \times {det}_{s} B \\ = {det}_{s} A \times (det B - v_{u} {det}_{s} B) + \times (det A - v_{u} {det}_{s} A) {det}_{s} B \\ det [\begin{array}{c} A & v_{u} \\ v_{u} & B \end{array}] & = det [\begin{array}{c} A_{v_{u}} & 0 \\ 0 & B_{v_{u}} \end{array}] + v_{u} {det}_{s} [\begin{array}{c} A & v_{u} \\ v_{u} & B \end{array}] \\ = det A_{v_{u}} \times det B_{v_{u}} + v_{u} {det}_{s} [\begin{array}{c} A & v_{u} \\ v_{u} & B \end{array}] \\ = (det A - v_{u} {det}_{s} A) \times (det B - v_{u} {det}_{s} B) + v_{u} {det}_{s} [\begin{array}{c} A & v_{u} \\ v_{u} & B \end{array}] \end{aligned}

于是就可以维护了。

2024.1.5

40 / 100 / 45, sum 185, rk 39/58

他妈 T1 被卡常卡成 40 分有点蚌埠住。custom test 比实际测评跑的快，因为实际测评一堆点并行跑，然后把我 cache 全挤掉了。呃呃。循环两维调换下位置快了一倍。T3 卡卡空间就过了。

T1 没啥意思，T2 挺简单的数位 DP，进位是一个前缀应该挺常见的了，稍微写下 T3。

R19 T3 树与

考虑一个 01-Trie 上的按位贪心，先看这一位全选 $1$ 的数量，即右子树大小，如果 $\geq m$ ，那么就可以直接向右子树走，否则此时可以在两个子树内走。但是此时有多个子树，并不好处理，不过注意到不往右走的情况右子树内数量 $< m$ ，于是我们可以把这 $m$ 个值暴力存下来，这样就不用管右子树了。这样最多存下 $(m - 1) \log V$ 个数，每一层暴力遍历一遍，这样单次查询复杂度 $O (m \log^{2} V)$ 。由于 $m$ 很小，这个复杂度其实是能跑的。链上查询直接可持久化 01-Trie 和树上差分即可。

但是问题是 01-Trie 的空间复杂度是 $O (n \log V)$ 的，无良出题人把这玩意空间给卡了。不过硬卡是能卡过去的，因为左右子树中至少有一个点的编号是当前点的编号 +1，于是可以仅记录一个儿子，一共需要 $20 + 1 + 26$ 位，可以使用一个 int 一个 short 存下。然后就能过了。

正经做法是，注意到上述做法访问到的点实际上只有前 $O (m \log V)$ 个数，于是如果我们能找到链上的前 $O (m \log V)$ 大的数，然后再用上述做法，就不需要把所有值全插入 01-Trie 了。找前 $O (m \log^{2} V)$ 大的值可以使用超级钢琴的做法，树剖一下然后用堆维护所有段，然后每次将一条链分裂成两部分，这样就变成了时间复杂度 $O (n + q m \log V \log (m \log V))$ ，空间复杂度 $O (n)$ 之类的东西了，我没写所以没仔细想。

把计数与数学 H 补了。

L1.3 T8 抽奖机

首先题目描述的就是个三进制异或 FWT，二进制异或 FWT 实际上是在对每一维做 DFT / IDFT，那么三进制同样做 DFT / IDFT 即可，三次单位根模 $P$ 存在，所以直接做。

注意到出现 $0, 1, 2$ 次数相同的一个集合，其系数均是相等的，那么我们可以记 $f_{a, b}$ 表示有 $a$ 个 $1$ ， $b$ 个 $2$ 的集合的系数，那么我们只需要把这个东西 FWT， $k$ 次幂，然后 IFWT 回去即可。

考虑对这个东西做 FWT，相当于将 $n - a - b$ 个 $0$ ， $a$ 个 $1$ ， $b$ 个 $2$ 进行重新分组，然后有一个系数，贡献系数可以由一个二元 GF 表示：

G_{a, b} (x, y) = (1 + x + y)^{n - a - b} (1 + ω_{3} x + ω_{3}^{2} y)^{a} (1 + ω_{3}^{2} x ω_{3} y)^{b}

这个东西是容易 $O (n^{2})$ 递推到下一项的，于是这样就可以 $O (n^{4})$ 递推出所有系数，这样就做完了。

2024.1.6

100 / 30 / 20, sum 150, rk 20/38

这个真蚌埠住了，NOI 前的 nfls 模拟赛教我了 bitset，教我了按 $w$ 分块卡空间，但是没教我原来 bitset 算空间需要先除以 $8$ 。我以为 ST 表一类的 $w \log w$ 个 bitset 根本开不下，于是写了线段树。结果线段树数组还开小了，因为我以为开 100 个 bitset 就 MLE 了。乐死了。

天天垫！

R20 T2 原神账号

卸载！

肯定是个 bitset，然后套路分块，但是不能差分，很恼，但是或可以重复贡献，ST 表即可。bitset 空间要除以 8，所以 8 MB 是可以开下的。我是傻逼。

R20 T3 肖芬途

我今天没喝冰红茶。

其实做法真的不复杂，我咋就不会呢。

容易发现这个限制实际上是给了一个 BFS 序，且注意到， $l$ 的限制将点集划分成了若干棵子树， $r$ 的限制则是往这几棵子树内加入了若干点，显然 lca 在区间内当且仅当两个点选在同一棵子树内，这样我们只需要知道每棵子树的权值和的平方和即可。而有贡献的子树只有 $f_{p} < l$ ，那么我们找到最大的 $p$ 使得 $f_{p} < l$ ，我们就只需要求仅保留 $[1, r]$ 的点时， $[l, min (r, p)]$ 内的所有点的子树和的平方和。如果可以离线，那么这容易使用扫描线解决。

强制在线比较恶心，这里有一个小技巧：我们把上述做法改成根号重构，每 $B$ 次直接重新处理一遍所有的子树和与平方前缀和，然后在这基础上再考虑加入 $B$ 个点的贡献，容易发现我们只需要找到每个点所在的子树即可，由于 $[l, min (r, p)]$ 内的点深度最多只差 $1$ ，我们可以先找到每个点的 $d e p_{l} + 1$ 处的祖先，然后判断一下是不是在区间内，不是则取它的父亲。写个 k 级祖先即可。然后你发现这个做法完全可以做强制在线，只需要把每次重构后的数组记录一下，然后每次询问把多的 $B$ 次暴力加上即可。复杂度 $O (n \sqrt{n \log n})$ 或 $O (n \sqrt{n})$ ，取决于 k 级祖先的实现。

我不理解为啥原题要卡树剖的 k 级祖先啊，而且大部分情况树剖跑的是比长剖快的，怎么感觉集训队互测都喜欢整一些无意义加强，净把一些好题给整成恶心人的题。

唉，晚上打 CF，水个题吧。

ABC335G Discrete Logarithm Problems

根据经典离散对数理论，直接离散对数，相当于求 $g^{b_{i} k} \equiv g^{b_{j}} (\mod P)$ ，即 $b_{i} k \equiv b_{j} (\mod P - 1)$ ，然后这玩意有解的条件是 $gcd (b_{i}, P - 1) | b_{j}$ ，容易发现我们只关心 $gcd (b_{i}, P - 1)$ ，我们令它为 $c_{i}$ ，则条件是 $c_{i} | c_{j}$ 。

直接求 $b_{i}$ 是不好求的，BSGS 啥的都不好使，但是注意到我们只在乎 $c_{i} = gcd (b_{i}, P - 1)$ ，如果 $c_{i} = 1$ 则 $a_{i}$ 是原根，类似地，可以得到 $a_{i}^{\frac{P - 1}{c_{i}}} \equiv 1 (\mod P - 1)$ ，这就容易判断了，我们每次可以除以一个质因子，然后看是不是 $1$ ，这样就可以 $O (\log^{2} P)$ 求出 $c_{i}$ 了。

然后问题就是有多少 $c_{i} | c_{j}$ ，由于 $c_{i} | (P - 1)$ ，不同的 $c_{i}$ 只有 $O (\sqrt{P})$ 个，于是我们可以直接做狄利克雷前缀和，然后计算答案即可。

2024.1.7

咋都会 F2 啊。

早上想了两个小时没有任何想法，然后看题解一个 hint 马上秒了，这个太深刻了。有种 noi d2t2 的美。但是这种很显然的转化根本想不到到底是怎么回事呢。

决定把标题里面的 nfls 删了，因为这博还是有点 nfls 以外的训练内容的。

CF1919F2 Wine Factory

考虑建个最大流的图， $S$ 向 $i$ 连 $a_{i}$ ， $i$ 向 $T$ 连 $b_{i}$ ， $i$ 向 $i + 1$ 连 $c_{i}$ ，那么显然答案就是最大流。

考虑最大流等于最小割，我们要找出这张图的一个最小割，容易发现相邻两个点 $i, i + 1$ 之间，如果 $i$ 割 $i \to T$ 且 $i + 1$ 割 $S \to i + 1$ ，那么此时仍然存在 $S \to i \to i + 1 \to T$ 的路径，于是需要把 $i \to i + 1$ 也割掉，否则就不割。显然可以写成一个 DP $f_{l, r, 0 / 1, 0 / 1}$ 表示区间左右端点分别割的哪个，然后直接上线段树维护即可。

Gym103371I Organizing Colored Sheets

沈老师题单题。

我们只需要考虑每个没被染色的格子可以由哪些大小的矩形覆盖，然后对所有的格子的矩形集合求交即可。

容易发现，我们只需要考虑与某个已经被染色的格子相邻的格子即可，因为假如某个大小的矩形能将所有与某个已染色格子相邻的格子全部染色，那么找到任意一个最大的包含一个格子的矩形，其一定与某个已染色格子相邻，将其进行一些平移即可将当前格子染色。

那么只需要考虑挨着某个染色格子的答案即可。假设是上边界挨着染色格子，我们可以直接枚举这个矩形的高度，然后找出以这个高度的最大矩形即可，这个是容易求的。注意到每一个未被染色的格子只会由上述过程枚举一次，所以复杂度是 $O (n^{2})$ 的。

QOJ1884 Mission Impossible: Grand Theft Auto

感觉沈老师课件的做法和过的几份代码基本没有什么道理，主要在于 $m$ 为奇数时覆盖坏边的处理，因为需要有一条路径同时覆盖坏边和最后一个叶子，而这两者同时覆盖必定有一个会被恢复掉，并没有想到合理的解决方案，有会的求教教。不过阅读一些代码找出了一个做法。

操作相当于有一棵树，初始全是黑色，每次将一条链染白，然后将所有黑点周围的白点染黑，使用 $⌊ \frac{m}{2} ⌋ + 1$ 次操作把所有点染白。

注意到这里不是 $⌈ \frac{m}{2}$ ，也就是说 $m$ 时偶数时实际上是有 $1$ 次多余操作的，考虑到让 $m \leftarrow m + 1$ 不会使得操作次数改变，那么我们从某个非叶子节点下挂一个叶子，这样就将问题规约到了 $m$ 是奇数的情况上。

简单手模一下发现，重点在于删除的叶子 DFS 序需要是连续的，因为如果一棵子树内的一个叶子被删，而还剩下一个叶子，那么如果下一回合不选这个子树内的叶子，那么下一回合被删除的叶子就可能恢复。那么我们考虑一种构造：按照 DFS 序列下每一个叶子，从某个点 $x$ 开始，按照 $(x, x + 1), (x - 1, x + 2), (x - 2, x + 3) \dots$ 的顺序依次选择每一条路径，最后剩下一个叶子直接覆盖叶子到根即可。

但是这样构造的问题是，如果某个 $(l, r)$ 路径正好是某个子树（或子树补）的最后两条路径，那么下一步就会往外（或往里）继续走，但是此时会有一个黑点进入刚覆盖完的子树（或子树补），此时这个点就永远不会被覆盖到了，因为子树内的叶子已经全部被覆盖过了。

我们大胆猜测，存在一个点这样做不会出现上述情况。我们需要更细致一些的考虑：首先，二度点是没有用的，我们可以将所有二度点全部缩起来，此时这棵树上最多还剩下 $2 m - 1$ 个点（实际上好像是 $2 m - 2$ 个，不过我懒得卡那么紧了），此时一共有 $2 m - 2$ 条边，注意到一条边只有一棵子树内叶子数是偶数，那么也就只能对应一种不被覆盖的边的情况，此时有 $m$ 个叶子 $2 m - 2$ 条边，其中一定有一个叶子至多被覆盖 $1$ 次。

还不够，注意到由于我们最后一次操作可以直接将一个叶子到根覆盖掉，那么也就是说如果子树内只有一个叶子，那么此时进行上述的限制是没有意义的。我们只考虑不连向叶子的边，此时仅剩 $m - 2$ 条边，故一定存在一个点没有任何一个限制，拿这个点来进行上述的简单构造即可。

2024.1.8

40 / 100 / 41, sum 181, rk 9/40

呃呃。

T3 好像有高级做法，不过好像所有人都是 KTT 或者分块凸包过的。额。

我不会 KTT 啊。我是不是应该抄一个。

唉抄个鬼，不如颓 project euler。

R21 T1 盗梦空间

简要题意：给你一棵树，每次询问 $k$ 个点，求一个点到 $k$ 个点中最近距离的最大值。 $n, \sum k \leq 10^{5}$

考虑建虚树，然后答案分三种情况：

在虚树点上：可以通过在虚树上 DP 得到；
在空子树内：直接预处理；
在虚树边上：考虑可以处理出每个点的兄弟子树内的最大距离，那么就可以倍增处理出一条链上的除链以外的子树内的最大深度，然后每个边上找到分界点即可。

唉，我的好做法：

考虑求出每个关键点管辖的连通块，其中这个连通块内的所有点的最短距离都是这个关键点，那么只需要求出每个关键点到其管辖的连通块内的最长距离即可。

连通块只需要找到虚树上每个点到关键点的最近距离，然后按照这个距离划分即可，虚树上两端管辖点不同的边中间的分界点容易找到。

然后考虑拿珂朵莉树来维护连通块的标号区间。注意到一个连通块的标号区间就是这个连通块最浅的点的子树区间删掉子树内其它连通块的区间，于是可以珂朵莉树维护。

找一个点到区间内的最远距离可以直接线段树维护直径。~~我使用点分树 $\log^{2}$ 卡常卡死我了。~~

R21 T2 偷藏女装 (ARC068F Solitaire)

但是我之前确实没看这个式子咋证明的。

洛谷题解看到一个比较简单的证明，写一下：

考虑合法序列的限制：前 $k - 1$ 个元素一定可以划分成两个下降序列， $k$ 一定是 $1$ ，然后剩下的序列一定小于其中一个序列的最小值，且每个点要不然是后缀最大值要不然是后缀最小值。我们考虑将最后一段先排好序，这样相当于整个序列可以划分成两个下降序列，然后乘上最后一段的方案数即可，最后一段显然可以选开头或者选结尾，方案数 $2^{n - k - 1}$ 。

现在问题是，求有多少长度为 $n$ 的排列，满足可以划分成两个下降序列，且 $a_{k} = 1$ 。有个结论：一个合法排列的逆排列也合法，因为题目要求的可以看作是二维平面上二维偏序的最小反链覆盖，这等于最长链，显然这个东西沿对角线翻转是不变的。那么我们只需要统计 $a_{1} = k$ 的最长链小于等于 $2$ 的排列数。

设 $f_{n, i}$ 表示长度为 $n$ ， $a_{1} = i$ 的方案数，那么答案就是 $f_{n, k}$ 。

若 $i = a_{1} = n$ ，那么此时这个点一定不可能出现在长度 $\geq 3$ 的链中，所以可以直接删去，此时 $a_{2}$ 可以是任意值，即 $f_{n, n} = \sum_{i = 1}^{n - 1} f_{n - 1, i}$ ；
否则，考虑 $a_{2}$ 的值：
- 若 $a_{2} = n$ ，同样这个点不能出现在长度 $\geq 3$ 的链中，可以删去，于是 $f_{n, i} \leftarrow f_{n - 1, i}$ ；
- 若 $a_{1} < a_{2} < n$ ，此时一定出现 $a_{1} - a_{2} - n$ 的链，不合法；
- 若 $a_{2} < a_{1}$ ，那么注意到如果 $a_{2}$ 存在于某条链中，那么可以把这个链的 $a_{1}$ 改成 $a_{2}$ ，最长链不变，所以可以把第一个数删去，于是 $f_{n, i} \leftarrow \sum_{j = 1}^{i - 1} f_{n - 1, j}$ 。

综上，我们有：

\begin{aligned} f_{n, n} & = \sum_{j = 1}^{n - 1} f_{n - 1, j} \\ f_{n, i} & = \sum_{j = 1}^{i} f_{n - 1, i} \end{aligned}

改变一下形式就是：

\begin{aligned} f_{n, n} & = f_{n, n - 1} \\ f_{n, i} & = f_{n - 1, i} + f_{n, i - 1} \end{aligned}

发现 $f_{n, k}$ 其实就是从 $(1, 1)$ 走到 $(n, k)$ 且不穿过 $y = x$ 的路径数，于是类似卡特兰数的方法计算即可。于是可以得到 $f_{n, k} = (\binom{n + k - 2}{k - 1}) - (\binom{n + k - 2}{k - 2})$ 。那么答案就容易计算了。

这个模数直接 exLucas 即可。

R21 T3 楼梯调度

首先有一个弱智的 $O (n^{3})$ DP，设 $f_{i, j, k}$ 表示考虑到 $i$ 两个序列最大值是 $j, k$ 。容易发现 $j, k$ 中一定有一个是当前的前缀最大值，所以只需要存其中一个，所以变成 $O (n^{2})$ 了。

仔细写一下 DP 式子，发现我们可以将这个 DP 看作下面的操作：

若 $a_{i} = p_{i}$ ：
- 全局加 $a_{i}$ ；
若 $a_{i} < p_{i}$ ：
- 求得 $[0, a_{i}]$ 内的最小值 $v$ ；
- 对于 $j \in [a_{i}, p_{i}]$ ，令 $f_{j} \leftarrow f_{j} + j$ ；
- 对于 $j \in [0, a_{i} - 1]$ ，令 $f_{j} \leftarrow f_{j} + p_{i}$ ；
- 令 $f_{a_{i}} \leftarrow max (f_{a_{i}}, v + a_{i})$ 。

这不是我们区间加下标区间求最小值吗，直接上 KTT 就完了。复杂度 $O (n \log^{2} n)$ 。正解跑的没这个快，嘲讽正解。

可是我不会 KTT 啊。其实 KTT 就是存一个一次函数 $k x + b$ ，然后存一个 $l i m$ 表示什么时候左子树的答案会比右子树优（注意到左面增加量比右边小，所以右边不可能会变成比左边优），即 $l i m = \frac{b_{l} - b_{r}}{k_{r} - k_{l}}$ ，线段树上的 $l i m$ 存这个区间内所有节点的 $l i m$ 的最小值，修改时如果 $x > l i m$ 就暴力向下递归计算，可以证明复杂度均摊是 $O (n \log^{2} n)$ 的，就是考虑一次势能减少需要遍历线段树上 $\log$ 个节点，然后每次修改势能也就增加 $\log$ ，所以复杂度 $O (n \log^{2} n)$ 。这是 $k_{i}$ 单调递增的特殊情况，如果 $k_{i}$ 任意，那么只能证明到 $O (n \log^{3} n)$ 。

2024.1.9

100 / 100 / 40, sum 240, rk 1/52

草。

T1 广义串并联图，T2 部分分式分解，T3 看着就不像是有啥人会做的样子，然后最后两个小时狂暴 T3 打表，有点乐。然后闲的没事就去 project euler 了。

唉我发现 project euler 真是好颓资，

R22 T1 染色问题

简要题意：求图的 $k$ 染色数， $n - m \leq 5$ 。

这个限制考虑无脑上广义串并联图方法。删一度点是容易的，缩二度点之后注意到这条边的两段的颜色有可能相同，于是我们设计权值 $(f, g)$ 表示两端点颜色不同的系数为 $f$ ，两端点颜色相同的系数为 $g$ ，初始所有边的权值均为 $(1, 0)$ 。

然后套做法：

删一度点： $a n s \leftarrow a n s \times ((k - 1) \cdot f + g)$ ；
缩二度点： $f \leftarrow (k - 2) f_{1} f_{2} + f_{1} g_{2} + f_{2} g_{1}, g \leftarrow (k - 1) f_{1} f_{2} + g_{1} g_{2}$ ；
叠合重边： $f \leftarrow f_{1} f_{2}, g \leftarrow g_{1} g_{2}$ 。

最后缩完之后剩下的图 $n \leq 10, m \leq 15$ ，直接搜剩下的图的最小表示即可。

R22 T2 IOer

简要题意：求 $[x^{n}] \frac{1}{\prod_{i = 1}^{m} (1 - (u i + v) x)}$ ， $n \leq 10^{18}, m \leq 10^{5}$ 。

直接分治乘法加线性递推肯定是常数极大不太好跑的，考虑找一些深刻的做法。

容易联想到我们求斐波那契数列的单点时，有一个通项公式可以通过部分分式分解求得答案，那么我们考虑类似的做法。考察假设最后有 $\frac{1}{\prod_{i = 1}^{n} (1 - a_{i} x)} = \sum_{i = 1}^{n} \frac{b_{i}}{1 - a_{i} x}$ ，满足 $a_{i}$ 互不相同，把左边的分母乘过去即可得到 $1 = \sum_{i = 1}^{n} b_{i} \prod_{j \neq i} (1 - a_{j} x)$ ，这个形式是很有趣的，我们带入 $x = \frac{1}{a_{i}}$ 之后可以发现后面只有一项不等于 $0$ ，即 $1 = b_{i} \prod_{j \neq i} (1 - \frac{a_{j}}{a_{i}})$ ，即可得 $b_{i} = \frac{a_{i}^{n - 1}}{\prod_{j \neq i} (a_{i} - a_{j})}$ 。

我们把相同的式子套过来，即可得到 $b_{i} = \frac{(u i + v)^{m - 1}}{\prod_{j \neq i} u (i - j)} = \frac{(u i + v)^{m - 1} (- 1)^{m - i}}{u^{m - 1} (i - 1)! (m - i)!}$ ，这个容易 $O (\log P)$ 计算，那么我们知道了这个系数，答案就是 $\sum_{i = 1}^{m} b_{i} (u i + v)^{n}$ ，这个也很容易计算，这样我们就可以 $O (m (\log P + \log n))$ 求得答案了。

其实 $u = 998244353$ 时会退化成求 $[x^{n}] \frac{1}{(1 - v x)^{m}}$ ，不过好像并没有卡这个（

R22 T3 力脑

简要题意：给定一个 01 串，有些位置是 ?，将 ? 随机替换成 0 或 1，求对这个字符串建后缀自动机的节点数期望。

考虑 SAM 节点数等于反串后缀树的节点数，所以我们先反转一波求后缀树的节点树。由于字符集为 2，所以这是一棵二叉树，我们记儿子数为 $0, 1, 2$ 的点分别为 $A, B, C$ 类点，其数量为 $a, b, c$ 。分析一下：

A 类点一定是这个串的某个后缀，且在整个串中仅出现一次；
B 类点一定也是一个后缀（否则会被压缩起来），且将这个后缀后面加一个 0 或 1 后，只有其中一种字符串存在。

C 类点没什么性质，考虑去掉它，由于 $b + 2 c = a + b + c - 1$ ，即 $c = a - 1$ ，于是我们只需要计算 $2 a + b - 1$ 的期望即可。

首先先考虑 A 类点怎么计算：我们考虑枚举这个后缀是什么，然后求出这个后缀仅出现一次的概率 $P (d)$ ，那么 $E (a) = \sum_{d = 1}^{n} P (d)$ 。（此处的后缀 $s u f (d)$ 指 $s [d, n]$ ）

考虑怎么计算 $s u f (d)$ 的概率，可以容斥考虑其是哪些 $s u f (i), i < d$ 的前缀，设后缀集合 $A$ ，记 $P r (A)$ 为 $s u f (d)$ 是 $A$ 中所有后缀的前缀的概率，那么有：

P (d) = \sum_{A} (- 1)^{| A |} P r (A)

考虑怎么求这个式子，我们有两种方法：

枚举 $A$ ：我们可以暴力枚举集合 $A$ ，这样我们可以确定一些字符相等的关系，我们把字符相等的缩起来，这样我们能够得到若干个连通块，我们只需要考虑每个连通块内字符相同的概率即可，复杂度 $O (n^{2} 2^{i})$ ；
枚举 $s u f (d)$ ：上一种做法是枚举 $A$ ，计算有多少后缀满足条件，我们可以改成直接枚举后缀是什么，然后看它是多少后缀的前缀，然后把容斥系数计算出来。这可以进行 DP，设 $f_{i}$ 表示考虑了 $s u f (1), s u f (2), \dots, s u f (i)$ ，且最后一个集合内选择的后缀是 $s u f (i)$ ，容斥系数之和。考虑从 $f_{i}$ 转移到 $f_{j}$ 的系数：
- 首先 $s [j, j + l e n - 1]$ 需要能和 $s [d, n]$ 匹配，否则肯定不能转移；
- 若 $j + l e n - 1 < i$ ，那么这两次匹配没有交，那么 $(j + l e n - 1, i)$ 之间的 ? 可以随便填，乘一个方案数；
- 否则，两者会存在一个 $j + l e n - i$ 的交，说明这个长度必须是 $s [d, n]$ 的一个 border，可以先对这个串跑 KMP 求出所有 border，然后就能快速判定了。
  这样的复杂度是 $O (n^{2} 2^{n - i})$ 。

容易发现我们只需要平衡一下两种算法，即可得到 $O (n^{2} 2^{\frac{n}{2}})$ 的复杂度。

考虑 $b$ 是啥，我们可以先往串后面加一个 0，如果 $s u f (d) + 0$ 只出现了一次，说明不存在 $s u f (d) + 0$ 这个串，但是这样可能把 A 类串算重，所以需要再减一下。后面加 1 同理。发现这样一减正好把 $2 a$ 减掉了，所以我们只需要求原串加 0 和原串加 1 的答案和即可。注意根节点可能是 B 类点，这时候只有全 0 或全 1 出现，可以特判掉，而这种情况的原因是空后缀没有考虑，所以也可以把空后缀的答案也算上，直接跑上述算法加上最后一个后缀的答案正好是对的。

2024.1.10

字符串专题。

但是讲课视频开头还有些似乎是上个专题没讲完的东西，那就：

L1.3 T? 好像是个 FWT 题

给定一个集合幂级数 $F (x) = \sum_{i = 0}^{2^{d} - 1} a_{i} x^{i}$ ，给定 $k$ 个位置 $b_{i}$ ，求 $\sum [x^{b_{i}}] FWT (F (x))$ ，这里的 $FWT$ 是异或 $FWT$ 变换。 $d \leq 23, k \leq 4096$ 。

首先考虑 $FWT$ 的式子： $[x^{i}] FWT (F (x)) = \sum_{j = 0}^{2^{d} - 1} [x^{j}] (- 1)^{parity (i & j)} F (x)$ 。

我们考虑对于每一个 $j$ ，找出有多少 $b_{i}$ 满足 $parity (b_{i} & j) = 1$ 就能 $O (2^{d})$ 计算答案了。考虑 bitset 维护，设 $S (i)$ 为 $parity (i & j) = 1$ 的 $j$ 的集合，考虑 $T (p)$ 为 $p$ 这一位为 $1$ 的 $j$ 集合，那么就有转移 $S (i) = S (i \oplus lowbit (i)) \oplus T (\lg (lowbit (i)))$ ，这样转移复杂度 $O (2^{d} \cdot \frac{k}{w})$ ，可以通过 $k$ 较小的部分。

考虑我们实际上在求什么，再设一个 $G (x) = \sum x^{b_{i}}$ ，那么我们所求的其实是 $FWT (F (x)) \cdot G (x)$ 。用线性代数语言来描述，即为 $a \times F \cdot b = a \times F \times b^{T}$ ，整个转置一下得到 $b \times F^{T} \times a^{T}$ ，由于 $FWT$ 矩阵是对称的，则 $F = F^{T}$ ，所以我们所求也等于 $FWT (G (x)) \cdot F (x)$ 。由于 $G (x)$ 的项数比较少，我们可以考虑用一些更快的方法求出它的 $FWT$ 。考虑我们暴力计算其中的 $d - c$ 位，剩下的 $c$ 位跑 $FWT$ ，那么复杂度就是 $O (k 2^{d - c} + 2^{d} c)$ ，取 $c = \log k$ 即可得到一个 $O (2^{d} \log k)$ 的复杂度的算法。

T? Strange Function

计算几何狗都不做。

好的回到字符串。

L1.10 T1 (P5829【模板】失配树)

有人说，这是一道模板题，所以我们使用 border series 解决这个问题。

唉就还是那套理论，然后当树剖写就行了。求一个 border 的最短的公差相等的 border，然后一直跳 top 就好了。

auto top = [&](int x) { return x <= 1 ? x : x % (x - nxt[x]) + (x - nxt[x]); };
while (m--) {
    int p, q; scanf("%d%d", &p, &q);
    p = nxt[p], q = nxt[q];
    while (top(p) != top(q)) {
      if (top(p) > top(q)) p = nxt[top(p)];
      else q = nxt[top(q)];
    }
    printf("%d\n", min(p, q));
}

长得挺好看。

L1.10 T2 (P4156 [WC2016] 论战捆竹竿)

考虑把所有 border 找出来，那么每次就是可以将字符串后面加一个 $n - b o r d e r$ ，然后问有哪些 $w$ 可以被得到。

显然是个同余最短路问题，但是 $O (n^{2})$ 肯定过不了。考虑到 border 可以划分成 $\log$ 段等差数列，而同余最短路可以把每一条边的转移分开考虑，那么我们依次考虑每段等差数列 $x + k d, k \in [0, l]$ 的转移。

这个首项 $x$ 很烦人，如果能够在模 $x$ 的意义下做这个同余最短路就简单多了，于是我们考虑每次转移的时候先将模 $l s t$ 的同余最短路变成模 $x$ 的同余最短路，然后再考虑怎么转移。这个过程相当于先用 $x$ 转移，此时关于 $x$ 一定满足同余最短路的性质，然后再改成模 $x$ 。首先 $d i s_{i}$ 肯定转移到新的 $d i s_{d i s_{i} mod x}^{'}$ 上，然后考虑到原来是模 $l s t$ 意义下的最短路，意味着我们可以任意加若干 $l s t$ ，那么我们再按照 $l s t$ 为边跑一遍同余最短路即可。

然后现在问题就是 $i \to i + k d$ ，边权为 $x + k d$ ，做同余最短路。考虑到 $i + k d$ 可以将 $[0, x)$ 划分成 $gcd (x, d)$ 个环，我们把每个环单独拿出来考虑。环上的转移并不好考虑，我们找到环上的最小值，显然这个值不可能会被更新，然后我们从这里断环为链，然后在链上做即可。这个过程显然可以单调队列优化。

复杂度 $O (T n \log n)$ 。

L1.10 T3 (P4548 [CTSC2006] 歌唱王国)

link

L1.10 T4 (HDU6791 Tokitsukaze, CSL and Palindrome Game)

额，结论和上题一样，所以比较的实际是两个 border 序列的字典序。

然后这个东西直接建 PAM 即可，哈希找下 LCP，倍增即可。

2024.1.11

string day2.

不知道为啥感觉巨累，不想写代码，摆了。

看 accoders 模拟赛题，感觉啥都不会，有点自闭。

upd. accoders $O (n^{3})$ 开 $n \leq 1000$ ，浪费我一个多小时感情，shaber。

L1.10 T5 (ROI 2016 DAY2 二指禅)

考虑 DP。由于每次可以加入一个前缀或一个后缀，我们正反建出两棵 Trie 树，然后考虑在上面转移。

加入一个前缀时，我们考虑从 $f_{i}$ 转移到 $f_{j}$ ，即从 $j$ 开始匹配，找到正 Trie 上的一个最长的匹配节点，然后我们可以从这些节点的任意一个节点进行转移。枚举可以匹配的 Trie 树节点，那么这个节点的子树内的所有串就都可以进行转移，我们找到权值最小的一个转移即可。当然这么整肯定复杂度不对，注意到这条链上子树内的字符串集合不同的节点只有 $O (\sqrt{L})$ 个，因为第 $i$ 个节点的子树内串长度至少为 $i$ ，而串的总和为 $L$ 。那么我们可以从下往上考虑，如果碰到新加入了一些串的子树，那么就将这个子树内权值最小的串进行区间转移，设这个点深度为 $d$ ，最小权值为 $v$ ，那么我们就可以转移 $f_{i} + v \to f_{i + [1, d]}$ 。

加入后缀也是类似的，我们考虑枚举 $f_{j}$ ，看哪些 $f_{i}$ 能转移到 $f_{j}$ 上，那么我们就是从 $j$ 开始向前匹配反 Trie 上的一个最长匹配节点，然后同样的做法，可以得到转移 $f_{i + [1, d]} + v \to f_{j}$ 。

上述一个转移需要 $O (n)$ 次单点查询， $O (n \sqrt{n})$ 次区间修改，一个需要 $O (n \sqrt{n})$ 次区间查询， $O (n)$ 次单点修改，区间操作可以变成前缀或后缀，于是两者均可分块把复杂度平衡掉。对于找最长的匹配节点，可以直接树剖二分哈希，或者把所有节点的哈希全插哈希表然后二分长度。复杂度 $O (n \sqrt{n})$ 。

L1.10 T6 (CF1483F Exam)

为啥总不会这个。

子串一定是前缀的后缀，可以直接枚举每个串的每个前缀，考虑其匹配的最长的一个后缀。显然更短的一定被包含在最长的后缀里面，我们只需要把这 $O (n)$ 个串拿出来即可，如果有包含关系需要去掉。找匹配建 AC 自动机即可。但是此时仍然有可能有在非同一位置上的两个串存在包含关系，如果一个串被别的串包含过那么这个串在当前集合中出现次数一定小于在这个串中的出现次数，于是可以树状数组维护出某个串在当前串中的出现次数，然后只统计出现次数相等的串即可。

2024.1.12

100 / 100 / 70, sum 270, rk 2/58

咋 T3 还能是我做过的原。「解题报告」[AGC022F] Checkers

这题我正经做也就能打 20 分走人了，所以真实排名应该是 rk8。咋还这么靠前。好像 T1, T2 写挂的巨大多。

R23 T1 星际逃亡

简要题意：三维坐标系上有 $n$ 个点，每个静止或匀速直线运动，给定每个点的初始坐标和初速度。你需要从点 $1$ 走到点 $2$ ，每次可以从一个点跳跃到另一个点，且你不能在同一个点上待超过 $s$ 秒。总代价是每次跳跃的最远距离，最小化总代价。 $n \leq 10^{3}$

首先肯定二分答案，发现两个点能相互到达的时间是一个区间，容易解方程得出。考虑到如果一个点能与另一个点相互到达，那么可以不断反复传送实现一直刷新时间，那么 $s$ 的限制只有在每个点不能到达任何其它点的时间间隔最大是 $s$ 。考虑每个点能到达其它点的连续时间一共有 $O (n)$ 段，在这些段中，如果能在 $t$ 时刻到达这一个点，那么从 $[t, r]$ 中的任意一个时刻都可以在这个点上，那么我们就只关心到每个段的最早时间，那么我们可以跑一个最短路，一共 $O (n^{2})$ 个点 $O (n^{2})$ 条边，复杂度 $O (n^{2} \log n \log V)$ ，由于将重合的段合并后剩下的段并不是很多，所以跑的很不满。

R23 T2 博弈问题

简要题意：两个人树上博弈，先手选一个 $x$ 后手选一个 $y$ 要求 $x \neq y$ ，权值为 $w_{x} \oplus w_{y}$ ，先手想最小化权值后手想最大化权值，对于每一个子树求结果。 $n, V \leq 10^{5}$ 。

考虑 dsu on tree 一波，这样我们只用考虑每次集合内加入一个数如何维护答案。

考虑按位贪心，如果某一位上一个节点内仅有一个数，那么对方选择的时候就必须需要选另一个子树内的数，于是发现先手一定会选择某个只有一个数的子树。如果所有子树都不止一个数，说明每个数都至少出现了两次，答案肯定是 $0$ 。

那么考虑对于每一个子树大小为 $1$ 的节点，维护它与其兄弟子树内的异或最小值，这样取所有这样的值中的最大值即是答案。考虑插入一个数时，如果插入的这个数到达了一个空子树，那么这个点就成为了子树大小为 $1$ 的节点，这时候 $O (\log V)$ 去兄弟子树查询一下答案即可，而如果插入的节点的兄弟大小为 $1$ ，可以直接 $O (1)$ 更新答案，这样上述一共仅更新 $O (\log V)$ 次答案，可以使用一个可删堆暴力维护最大值，这样复杂度是 $O (n \log^{3} n)$ 的，你可以 Trie 上直接维护子树内的答案最大值就是 $O (n \log^{2} n)$ 的，唉我拿堆干啥。好像可以直接类似于线段树合并的方法合并两棵子树的 Trie，咕了。

2024.1.13

100 / 100 / 60, sum 260, rk 7/50

T1 T2 很无聊，而且下午放假，所以咕了。

2024.1.15

100 / 80 / 10, sum 190, rk 40/75

T1 结论很显然，T2 插头 DP 板子，T3 SoyTony 说讲课讲过，不过我没听，还是比较有趣的。不过挂分挂的太好了。

R25 T3 Dark Blue (GYM102803E)

首先考虑 height 全部确定怎么做，显然相当于有若干位置相等，还有若干不等关系，我们可以考虑并查集把相同的位置缩起来，然后不等关系建 DAG，然后拓扑 DP 一下即可得到最小方案。直接考虑的话，相等关系是若干个子串相等，可以并查集倍增做，不过本题有更优美的性质，由于 height 数组已经给出来了，可以考虑 SA 上由 height = 0 的部分划分成了若干段，其中每一段的开头字母显然是相同的，不同段之间字母显然不同，这样就很容易得到相等关系了，然后直接从前往后依次填 abcd 就是答案了。

考虑 height 有不确定的怎么办，那么我们同样可以将相等关系看作 SA 上的若干段开头相等，只不过这时候没有所有段互不相同的限制了。考虑不等关系，对于 height 相等的串不等关系很显然，height 不确定的话，我们考虑如何刻画两个子串的大小关系。虽然只给出两个子串的大小关系很难确定两个子串分别是什么，但是注意到我们有所有后缀之间的大小关系，也就是说如果两个后缀的大小关系只取决于两个后缀的首字母，如果首字母相等，则其大小关系取决于删去两个首字母后的两个后缀的大小关系，否则直接取决于首字母关系。那么我们就很容易得到不等关系了，只需要看看 rk[sa[i - 1] + 1] 与 rk[sa[i] + 1] 的关系，即可确定 $s_{s a_{i - 1}} \leq s_{s a_{i}}$ 或者 $s_{s a_{i - 1}} < s_{s a_{i}}$ 的不等关系，容易发现这个不等关系是个 DAG，直接按照 SA 的顺序从前往后贪心填即可。

2024.1.16

额这场直接挂机了，T1 T2 都做过，T3 看着像原神题，就一个挺麻烦的树剖然后就做完了呃呃。而且大样例内答案不为 $0$ 的值只有不超过 $40$ 个，感觉暴力能过，呃呃

不如做题单了，字符串专题还两题呢明天要开新专题了

L1.10 T8 (CF1276F Asterisk Substrings)

首先把本质不同的串分成几类，s s* *s s*t，还有一个空串一个 *。

前面几种都很好统计，分别是 $S [1, n]$ 、 $S [1, n - 1]$ 、 $S [2, n]$ 的本质不同子串数，考虑 s*t 怎么计数。

考虑对于每一个串 s 统计串 t 的合法数量。我们找出串 s 的 endpos 集合，那么串 t 一定是 endpos 集合中某个位置 $+ 2$ 开头的一个串，那么我们要求的就是若干个后缀的本质不同前缀数，发现这很容易用 SA 求出来，于是可以暴力写个后缀树上 dsu on tree 即可求出答案，或者用线段树合并来维护。

有篇题解说可以不用 SA 而是对反串求 SAM 然后线段树合并，其实这两者是完全等价的，因为 SA 的 height 就是后缀树上相邻两个儿子的 lca 深度，求若干个链并与 SA 相邻两两减去 lcp 长度是一模一样的。

2024.1.17

csy 计数专题：四个正常题，三个析合树计数，两个 q-analog，一个 ei 题。

额。

L1.17 T1 (Gym102538H Horrible Cycles)

感觉这题之前做过，但是不知道啥时候。

肯定先给 $a_{i}$ 排个序。对环的 DP 常见方法是记链数，那么考虑 $f_{i, j}$ 表示考虑左部前 $i$ 个点，右部 $a_{i}$ 个点，当前有 $j$ 条链，每次先选择右部 $a_{i + 1} - a_{i}$ 中若干个点形成新段，然后选择左部点将两条链合并或不合并，如果仅剩一条链可以形成环，然后直接 DP 就好了。

L1.17 T2 (AT_hitachi2020_f Preserve Diameter)

好好好

首先最后的图里直径只有一条，因为如果有两条可以加一条边把一条直径杀了但是图直径长度不变。

考虑现在找出这样一条直径，从直径一段开始 bfs，找到每个点到这个端点的最短距离。由于题目中要求加任意一条边都会使得直径改变，所以我们必须将不改变直径的边全部加上。我们按照距离相同的点分层，注意到在同层与邻层之间连边是不会改变任何点的最短距离，也就不会改变直径长度，于是这样的边一定全部会连上，且此时不可能出现跨两层之间的连边，因为这样会改变最短路径。那么，如果我们确定了每个点到这个端点的最远距离，则这个图的形态就确定了，于是我们只需要计数合法的距离数组即可。

对距离数组的限制有两个，一个是距离为 $0$ 与距离为 $d$ 的点分别只有一个，因为只有一条直径，而另一个是原树上的限制，因为原树上的边一定存在于最后的图中，必须满足原树上的边是同层或邻层之间的边，也就是两个点的距离差绝对值不超过 $1$ 。

我们考虑以直径中点为根进行 DP，因为这个中点一定被所有直径经过。设 $f_{u, i, j}$ 为 $u$ 子树内可能能作为距离为 $0$ 的点有 $i$ 个，可能作为距离为 $d$ 的点有 $j$ 个，即直径的两个可能端点各有多少。一开始令深度为 $\frac{d}{2}$ 的点为可能的点，每次决策一条边是同层还是邻层，如果是同层那么所有点都不可能作为直径的端点（距离中点小于 $\frac{d}{2}$ ），否则要不然距离为 $0$ 的点清空，要不然距离为 $d$ 的点清空。注意到由于最后我们只要两种可能点各 $1$ 个的方案数，于是 $\geq 2$ 个的方案是等价的，我们不关心具体有多少，于是 $i, j$ 都只需要开到 $3$ ，转移比较简单。

由于直径从哪头开始并不重要，所以答案需要除以 $2$ 。注意到可能直径中点是一条边，那么我们可以从这条边两端各 DP 一次，然后把两边的其中一种点只有 $1$ 个的方案乘起来，因为这条边会使得其中一种点变成 $0$ ，所以另一种点可以有任意多个。

2024.1.18

又看了 accoders 模拟赛，又啥都不会，又自闭了

L1.17 T4 (CF1450H2 Multithreading (Hard Version))

这题挺有趣的。

upd. fzj 说这题没趣

首先考虑固定局面如何计算答案。容易发现如果一段连续段长为偶数，那么我们可以内部任意匹配，一定可以将这一段消掉且不造成任何贡献。那么我们考虑每次删除相邻的两个同色点，这样一直删直到剩下的点为黑白交替，答案就是白点的数量除以 $2$ 。考虑将位置按照奇偶性分开，那么发现每次删除的两个点位置奇偶性一定不同，而最后剩下的白点奇偶性就是全部相同的，我们设奇数位置上的白点有 $x$ 个，偶数位置上的白点有 $y$ 个，那么答案就是 $\frac{| x - y |}{2}$ 。

考虑带问号，我们可以先将所有奇数位置上的问号染白，把偶数位置上的问号染黑，这样我们得到一个初始的 $x - y$ 的值 $w$ 。此时我们每翻转一个问号处的颜色就会使得 $w$ 减少 $1$ ，那么枚举翻转多少问号即可得到答案 $\frac{1}{2^{q}} \sum_{i = 0}^{q} [2 | (w - i)] (\binom{q}{i}) | w - i |$ 。注意由于要求合法方案，所以只有一半 $i$ 可以被选，所以一共有 $2^{q - 1}$ 种选择方案。那么就可以 $O (n)$ 计算答案了。

考虑如何修改。注意到修改之后 $w, q$ 的变化都是 $O (1)$ 的，于是我们可以考虑找一下答案的变化。先化简一下式子，把绝对值拆开，容易得到若干个形如 $\sum [2 | (w - i)] (\binom{q}{i})$ 与 $\sum [2 | (w - i)] (\binom{q}{i}) i$ 的式子。首先后面那个直接吸收一下就和前面那个一样了，对于前面这个式子来说我们可以把 $(\binom{q}{i})$ 拆成 $(\binom{q - 1}{i}) + (\binom{q - 1}{i - 1})$ ，这时候发现加上前面那个二的倍数的限制，恰好将每一个 $(\binom{q - 1}{i})$ 取了一遍，那么我们就是要维护一个组合数前缀和了。 $O (1)$ 维护组合数前缀和变化量是经典的，然后这题就做完了。

P3236 [HNOI2014] 画框

这个做法好厉害。

首先根据这篇博的第一个题的结论，我们只需要直到最后所有可能的 $(a, b)$ 的凸包即可。考虑一种神奇的算法，我们先找到 $a$ 最小的点与 $b$ 最小的点，这两点肯定在凸包上，然后我们每次找到这两点之间距离这两点形成的线段最远的一个点，即找到一个点 $p$ ，使得 $| (l - p) \times (r - p) |$ 最大，其中 $\times$ 是叉乘。显然这个点一定是凸包上两点之间的某个点，然后再两端递归下去，不断进行这样的操作即可找到凸包上所有的点。拆一下式子，发现相当于最大化 $x (y_{l} - y_{r}) + y (x_{r} - x_{l}) + x_{l} y_{r} - x_{r} y_{l}$ ，后面是一个常数，而前面的贡献可以拆到每一条选择的边上，那么我们也就是给每条边赋了一个权值 $a_{i} (y_{l} - y_{r}) + b_{i} (x_{r} - x_{l})$ ，然后求最小权完美匹配，直接做即可。复杂度 $O (| V | n^{3})$ ，其中 $| V |$ 是凸包的点集大小，有结论值域范围为 $V$ 的凸包点数最高是 $O (V^{\frac{2}{3}})$ ，可以接受。没卡 KM 的 $O (n^{4})$ 写法，不过费用流很难跑过去。

2024.1.19

100 / 100 / 65 / 10, sum 275, rk 21/82

THUWC 前的 IOI 赛制场，前三题是 GDKOI Day2，第四题是 Day1 T3。

T3 有点蚌埠住，之前做过一道和这题正解 90% 重合的题，然后我不知道可以代入单位根然后求和，呃呃了。

T2 找规律做的，可以大概猜到倍增然后往上面凑的，所以就懒得写了，T3 和上面那题不一样的一点就是答案求的是 $F (x)$ 下标为 $m$ 的倍数上的系数和，这等于 $\frac{1}{m} \sum_{i = 0}^{m - 1} F (ω_{m}^{i})$ ，然后就和那题做法一模一样了。

T4 看不懂，摆了。

2024.1.20

100 / 100 / 32 / 60, sum 292, rk 30/74

T3 成功推出了一般图最小点覆盖！然后下午才意识到原来是二分图。脑瘫。

T1 一开始想假了然后整了 1h 才过，呃呃。

T2 写 floyd 找环写了一年，因为点数 $2 n$ 跑不动，然后又卡了半天意识到可以把点数缩成 $n$ ，然后还 WA，手写 checker 拍了半天才过，一共麻了。

T3 没仔细看。但是仔细看了也不会，下午瞎写了个建模结果还假了。不会流阿！！！

T4 lxl。

R28 T3 deadline

还是不会。

考虑特殊性质二，相当于选择右部点每个点与左部点哪个点进行匹配，而左部点如果有一个点已经被匹配了那么右部点可以选这个点从而不增加贡献，那么我们考虑转化成左部点之间连边，然后要求每条边两个端点中至少选一个点，最小化点数，注意到新的图仍然是二分图，于是二分图最小点覆盖可以变成求最大匹配。

一般情况也是类似的考虑，新的限制相当于两个集合中至少有一个集合内有点，考虑给每个题目建一个点 $x_{i}$ ，然后将每个时间拆成两个点 $p_{i}, q_{i}$ ，让 $p_{i} \to q_{i} : 1$ ，如果 $t_{i} = 0$ 则 $S \to x_{i} : 1$ ，否则 $x_{i} \to T : 1$ ，对于每一个二元组，如果 $t_{u_{i}} = 1$ 则 $x_{u_{i}} \to p_{v_{i}} : \infty$ ，否则 $q_{v_{i}} \to x_{u_{i}} : \infty$ 。从最小割来理解，如果一个时间选择的集合内所有点已经匹配完了，那么已经无法到达这个点了，则不造成贡献；否则，就进行匹配。

唉好像大概是这么个意思，我没懂这个建模咋出来的，反正好像挺对的

感觉需要加训一下流与图匹配相关内容啊！

2024.1.21

白天摆大烂了，本来想写那个 B 题结果又没写，做了一上午加半下午的数列不等式题，感觉有一定意思，但好像也不多。晚上打 ARC，很感动的没下分。

不过好像题没有很有趣的所以就不写了。

2024.1.22

额不想写了，不知道为啥又巨累，上午基本摆了。T3 正解但是少了几种情况，调了半天也不会最后摆烂了。T2 实在不想写这种仔细卡状态大小的题了。

不知道为啥最近感觉非常累，唉直接摆烂到 THUWC & WC 吧，两个 WC 完了就放假了，也挺好的

R29 T3 哈夫曼回路

简要题意：有 $n$ 个矩形从左到右依次排列，下边界在同一条直线上，每次询问一个区间内的矩形，从某个点开始走一条最短的路径，使得这个区间内的矩形的每一条边被至少覆盖一次，输出这条最短路径的长度。

考虑每一条边至少覆盖一次是个很不好的东西，不过我们考虑一条边如果被经过了多次，我们把经过多次看作重边，这样相当于加若干条边，使得每条边恰好经过一次，这个东西显然是欧拉路径，只需要奇点个数为 0/2 即可。而仔细分析，发现每两个相邻矩形恰好会产生两个奇点，我们可以把这些奇点全部拿出来，恰好可以形成一个 $2 \times (n - 1)$ 的网格图，那么问题就是在这个网格图上选若干条边，使得度数为偶数的点为 0/2 个，最小化边的数量。显然可以考虑 DP，大致是考虑 $f_{i, 0 / 1, 0 / 1, 0 / 1 / 2}$ 表示前 $i$ 列点与之间的边确定了，然后第 $i$ 列点的两个点的度数奇偶性为 $0 / 1$ ，此时选了 $0 / 1 / 2$ 个偶数点。容易发现是一个 min-add 矩阵的转移。同时注意到当第三维为 $0 / 2$ 的时候前两维只有 $0, 0$ 和 $1, 1$ 两种情况，第三维为 $1$ 时只有 $0, 1$ 和 $1, 0$ 两种情况，那么实际上只有 $6$ 种状态，记矩阵大小 $d = 6$ 。

区间查询显然可以线段树上矩阵，建树复杂度 $O (n d^{3})$ ，朴素实现单次查询是 $O (\log n d^{3})$ 的，这里有常见 trick 是因为你要算的是一个向量乘若干矩阵，向量乘矩阵是 $O (d^{2})$ 的，于是你可以每次计算向量乘矩阵而不是把矩阵都乘起来再乘向量，这样复杂度就是 $O (\log n d^{2})$ 了，总复杂度 $O (n d^{3} + q \log n d^{2})$ 。

唉 nfls 群里有人因为开大时限让 $O (q \log n d^{3})$ 或矩阵 $d = 12$ 的做法过了，然后在群里开始阴阳。只能说水平高不代表素质高。屏蔽了。

CF1375G Tree Modification

我草 anton 还是太智慧了。

考虑以 $c$ 为根，然后观察每个点的深度变化。发现， $b$ 的子树内（除 $b$ 外）所有点的深度全部减 $2$ ， $b$ 的深度减 $1$ 。先别急着想换根 DP 或者贪心啥的，你发现只有一个点的深度的奇偶性发生了变化，我们随手给数黑白染色一波，很快啊！发现每次操作后只有一个白点变成黑点或一个黑点变成白点，那么显然我们只需要让黑点或者白点的数量变成 $1$ 即可，答案就是黑点白点的数量最小值减 $1$ 。显然黑点或白点数量为 $1$ 的情况只有一种，这个过程一定可以达到黑点或白点数量为 $1$ ，于是最后一定就是所求的情况。

2024.1.23

100 / 100 / 100? / 35, sum 335, rk 5/76

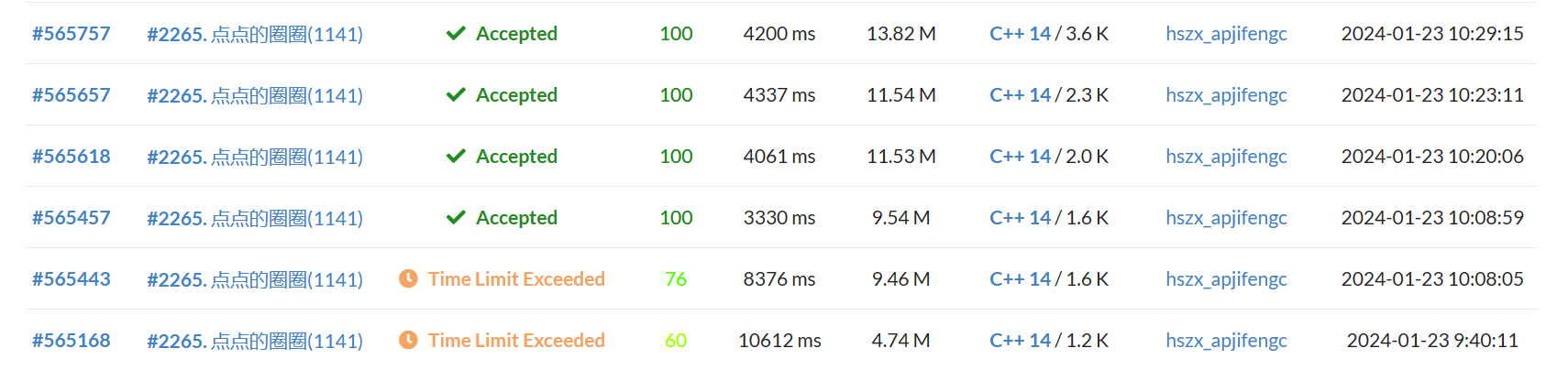
从下到上依次为：朴素 $O (n^{2})$ ，按 $x$ 扫，按 $y$ 扫（对他过了），还有若干发随机旋转。

乐。

唉感觉这个排名浮动还是挺乐的，打的各种玄幻。

R30 T3 点点的圈圈

简要题意：给 $n$ 个圆，圆之间互不相交或相切，每个圆有权值，选出互不包含的若干圆，求最大权值和。

首先发现这是一个类似于最长反链的东西，不过有一个最大权，但是本质其实还是相同的，简单推一下线性规划的对偶就发现这个问题的对偶问题是选出最少条链，使得每个点至少被覆盖 $w_{i}$ 次，原题给出的显然是一个树的限制，那么树上直接贪心即可，如果子树内向上的链已经能覆盖就不管，否则加一些链。

重点在于如何建树。

我们充分发扬人类智慧：
将所有点全部绕原点旋转同一个角度，然后按 $x$ 坐标排序
根据数学直觉，在随机旋转后，不在圆内但 $x$ 坐标与圆重合的点肯定不会太多
所以我们取相邻区间内的所有点进行 check
这样速度快得飞起，在 $n = 100000$ 时都可以在 1s 内卡过

额当然不是这么做，考虑扫描线，我们从左到右做扫描线，每与一个圆左侧相切时加入这个圆，右侧相切时删除这个圆。注意到与圆的交点之间的相对位置关系是不会改变的，那么我们可以维护所有交点，然后类似于维护一个括号序列。插入一个圆相当于在某个位置插入一对括号，然后问包含这个括号的父亲括号节点是什么。我们找出这对括号的前驱，如果这是一个左括号，那么说明这个括号就是包含它的点，直接设父亲为它，如果是右括号说明是它的兄弟，父亲设为它的父亲即可。拿个 set 维护即可，复杂度 $O (n \log n)$ 。

CF103E Buying Sets

SoyTony 跟我说半天直接建模就完了，我真的不会直接建模，不过整了好久之后得到了一个不是直接建模的做法，但是其实感觉好像比那个神秘建模想法要自然很多。

首先显然可以建二分图，题目中给的条件就是存在完美匹配。那么我们先随便找一组完美匹配，然后尝试将限制往完美匹配上凑。

注意到，如果左部点一个集合与其邻域大小相等，那么此时这个邻域恰好就是左部点所匹配的所有点。假设说邻域比左部点集合大小大，那么说明左部点一定有一个点连向了一个不是这个集合内的匹配点的点，那么此时我们可以钦定必须选上这个点在左部点中对应的匹配点。即，如果左部点集合内选 $i$ ，那么对于所有相连的右部点 $j$ ， $m a t c h_{j}$ 一定被选，容易发现满足这样的条件的集合一定是一个合法集合。那么我们直接跑最大权闭合子图即可。

posted @ 2024-01-01 19:52 APJifengc 阅读(775) 评论(5) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· NOI 2024 前做题纪要

· 2024.2 训练纪要

· 2024.4 ~ 若眨眼一瞬定能像星辰般飞向宇宙

· 2023CSP 前总结

· 2024.09 记录

阅读排行：
· 地球OL攻略 —— 某应届生求职总结
· 周边上新：园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源！
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】