5.2023.10 做题纪要 #32023-10-25

6.2023.11 做题纪要 #12023-11-06 7.2023.12 做题纪要 #12023-12-11 8.2023.12 做题纪要 #22023-12-19 9.2024.1 训练纪要2024-01-01 10.2024.2 训练纪要2024-02-15 11.2024.3 做题纪要2024-03-19 12.2024.4 做题纪要2024-04-07 13.NOI 2024 前做题纪要2024-05-25

2023.10.23

CSP。

P9755 [CSP-S 2023] 种树

考虑二分答案，设最后答案为 $p$ ，那么也就是说对于每一个 $u$ ，设其种的时刻为 $k_{u}$ ，那么有 $\sum_{i = k_{u}}^{p} max {b_{u} + c_{u} i, 1} \geq a_{u}$ ，容易发现这样的 $k_{u}$ 存在一个上界，设这个上界为 $t_{u}$ ，那么现在问题就是求是否存在一种树上拓扑序 $k_{u}$ ，满足 $k_{u} \leq t_{u}$ 。

考虑一个显然的贪心，到 $t_{u}$ 小的点肯定要尽可能早的选，如果没有树的限制那么从小往大选一定是最优的，但是这里有树的限制。有个经典 trick：设当前 $t_{u}$ 最小的点为 $x$ ，那么当 $f a_{x}$ 这个点被选择了之后，下一个选的一定是它，因为当前选它一定成为了最优解。那么我们实际上可以将这个点与父亲合并。那么就可以并查集维护每个连通块的大小 $s i z$ 和 $t_{u}$ 的上界 $v a l$ ，这样每次将 $u$ 合并到 $v$ 上时，由于 $v$ 选完之后才会选 $u$ ，那么 $u$ 的上界变成了 $v a l_{u} - s i z_{v}$ ，然后再与 $v a l_{v}$ 取 $min$ 即可。我们拿一个堆维护所有连通块，每次将 $v a l$ 最小的一个与父亲合并即可。如果最后的上界 $\geq 1$ 那么就是合法的，否则就不合法。复杂度 $O (n \log^{2} V)$ ，可以将二分的部分改成直接解方程找 $t_{u}$ ，这样就是 $O (n \log n \log V)$ 了，不过好像意义不大。

ABC304Ex Constrained Topological Sort

额。

所以上面这玩意可以直接加强到 DAG 上哈哈。

首先注意到一件事情，就是如果 $u \to v, R_{u} \geq R_{v}$ ，那么这时候 $R_{u}$ 的上界是不可能能取到的，因为一定有 $P_{u} < P_{v} \leq R_{v} \leq R_{u}$ ，所以我们可以将 $R_{u}$ 放缩到 $R_{v} - 1$ 。反向拓扑排序之后，我们可以转化成所有的 $R_{u} < R_{v}$ 的问题。

那么肯定还是要贪心的按照 $R_{u}$ 从小往大选，而注意到任意时刻下 $R_{u}$ 最小值一定是可以选的点（否则其一定是某个没选的点的后继，此时它不可能为最小值），于是如果没有 $L_{u}$ 的限制，那么就可以直接贪心了（对，这就是上一题），而加上 $L_{u}$ 的限制实际上直接贪心也可以，在决定第 $i$ 个是谁的时候找出所有 $L_{u} \leq i$ 的最小的 $R_{u}$ 即可，正确性也是显然的。

2023.10.24

好困。

内心又开始恐惧了，真心害怕这种“完全在能力范围内的题考场上做不出来”的情况再次发生。

快进到流浪街头憋屈致死。

今天才发现投计蒜客的那个题已经考完了，但是我也没号所以也看不到都打成啥样（yspm 给我投的），扔个链接在这里吧。

AGC019E Shuffle and Swap

还是比较简单的。

首先顺序肯定没有关系，那么我们假设一共有 $n$ 个 $1$ ，其中有 $m$ 个 $1$ 在另一个字符串上为 $0$ 。观察上面的操作，发现对于这 $m$ 个 $1$ 来说，它必须将这个 $1$ 放到某个需要有 $1$ 的位置上，而它要不然直接放到对应的 $B$ 的位置上，要不然可以选择让前 $n - m$ 个 $1$ 挪到一个 $B$ 的位置上，然后再让它挪到那个 $1$ 上。也就是说，实际上这 $m$ 个 $1$ 每一对都对应着一条链。我们设这些链的长度分别为 $k_{i}$ ，没有在链上的有 $k_{0} = n - m - \sum k_{i}$ 个，那么答案实际上就是：

(\binom{n - m}{k_{0}, k_{1}, \dots, k_{m}}) (k_{0}!)^{2} \prod_{i = 0}^{m} k_{i}! m! (\binom{n}{k_{0}, k_{1} + 1, k_{2} + 1, \dots, k_{m} + 1})

整理一下发现答案就是：

n! m! (n - m)! \prod_{i = 1}^{m} \frac{1}{(k_{i} + 1)!}

那么我们只需要对于所有的 $\sum_{i = 1}^{m} k_{i} \leq n - m$ 的 $k_{i}$ 求出上面的和即可。直接 DP 是 $O (n^{3})$ 的，不够优秀，考虑暴力上个 GF 刻画，上面那玩意的 GF 就是 $\frac{e^{x} - 1}{x}$ ，那么要求的就是 $(\frac{e^{x} - 1}{x})^{m}$ 的前 $n - m$ 次项系数之和，等于求 $(e^{x} - 1)^{m}$ 的前 $n$ 项系数之和，直接二项式定理展开就可以得到答案等于：

\sum_{i = 0}^{m} (\binom{m}{i}) (- 1)^{m - i} \sum_{j = 0}^{n} \frac{i^{j}}{j!}

直接求就是 $O (n^{2})$ 的，然后做完了。

AGC017F Zigzag

考虑一个朴素状压：设 $f_{i, S}$ 表示从左往右已经填到第 $i$ 条线，且最后一条线为 $S$ 的方案数。直接转移是 $O (4^{n} poly (n))$ 的。

那么考虑轮廓线 DP，每次只填一个数，这样我们已经填好的这些位置的左边的线段位置就不需要记录了，我们只需要记录一下左边那条线的横坐标即可，这样复杂度就变成了 $O (2^{n} n^{3})$ ，但是还是无法接受。

考虑将记录左边线的横坐标这一部分删掉。发现如果左边那条线在当前点的左边，那么这条线其实就没有用了，因为向左一定不会到达这条线，那么我们其实可以将这条线给向右折过来，这样就一定为完整的一条线了，那么就不需要记录横坐标了，于是复杂度 $O (2^{n} n^{2})$ ，可以通过。

CF1827E Bus Routes

首先容易发现如果叶子之间连通了那么所有点就都连通了，于是我们只需要考虑叶子，也就只需要考虑所有以叶子开始的路径。

考虑随便找一个根，然后求出每个叶子经过一条路径能到达的最浅的点，记这个点为 $f_{u}$ ，那么如果存在两个叶子 $u, v$ 满足 $f_{u}, f_{v}$ 没有祖先关系，那么这两个点就一定不能互相到达。而如果全部为祖先关系的话，发现所有的 $f_{u}$ 形成了一条链，那么我们只需要找到 $f_{u}$ 最深的一个 $r$ ，然后判断是不是所有点都能到达 $r$ 即可，因为如果一个点能到达 $r$ 那么它一定能到达所有 $f_{v}$ 比 $f_{u}$ 深的点，也就一定能覆盖所有情况。那么我们以 $r$ 为根在跑一边上面的算法，看所有叶子能到达的最浅的点是不是都是 $r$ 就行了。实现上我们可以不判断第一个条件，因为第一个条件不满足那么后面的条件也一定不满足，构造只需要找到 $f_{u} = r, f_{v}^{'} \neq r$ 的两个点 $u, v$ 即可。

2023.10.25

美好的一天从美好的一天开始！

不知道应该从啥开始，放只科米吧

P8426 [JOI Open 2022] 放学路（School Road）

咱就是说没事别这么折磨自己行不。

广义串并联图方法学习笔记。

这个从部分分一步一步分析。

$m \leq 40$ ：

发现 $m$ 很小，所以可以考虑爆搜出所有可能的简单路径。经过一些分析可以发现这样的简单路径最多 $2 \times 10^{6}$ 种，所以直接搜即可。

$n \leq 18$ ：

首先我们肯定只需要找出 $1 \to n$ 的最长路是不是等于最短路，那么直接状压 DP 即可，复杂度 $O (n^{2} 2^{n})$ 。

$m - n \leq 13$ ：

这就是本文所说到的方法了，考虑直接删一度点缩二度点叠合重边，那么最后的 $m \leq 42$ ，再用上述的做法做即可。注意 $1, n$ 不能被删或被缩。

具体来讲，删一度点直接删就行，叠合重边的时候如果两条边的长度不相等，那么就将这条边的边权设为 $- 1$ ，只要存在一条经过 $- 1$ 的路径那么就一定存在长度不等于最短路的路径了。缩二度点就是如果有一个为 $- 1$ 那么它也是 $- 1$ ，否则为两条路径长度的和。

图为点双连通分量：

注意到如果上述算法最后仅剩下一条边且不为 $- 1$ ，那么答案就一定为不存在，那么我们大胆猜测，如果最后不只剩下两个点一条边答案就为存在。

虽然这个结论并不在一般图上成立，但是可以证明它在点双上是成立的。~~或者由于它给出了点双的部分分，你猜测它在点双上是成立的。~~

证明

考虑如果最后剩下若干个点，那么这些点除了 $1, n$ 外，所有点的度数均 $\geq 3$ 。

我们首先给这张图定向，方向为最短路的方向，即 $dis (1, u) + w + dis (v, n) = dis (1, n)$ 的方向。如果不能这么定向那么答案肯定就是存在了。

如果一个点入度小于出度，我们称其为红点，否则称其为蓝点。

考虑 $1 \to n$ 中经过边数最多的一条路径，那么对于这条路径上的第一个点，其入度一定为 $1$ ，否则一定可以从 $1$ 经过若干个点再到这个点上，所经过的边数会更多。那么，这个点一定是一个红点。同理，路径上最后一个点一定是一个蓝点。

那么在这条路径上，一定存在一条边 $u \to v$ 满足 $u$ 为红点且 $v$ 为蓝点。那么一定存在 $u \to x$ 与 $v \to y$ 两条边，那么考虑 $1 \to y \to v \to u \to x \to n$ 这样一条路径，可以发现这样一条路径一定是简单路径，否则说明 $1 \to y$ 与 $x \to n$ 的路径上有重合点 $z$ ，这样 $1 \to x \to z \to y \to n$ 这条路径经过的边数更长，与假设矛盾。而这条路径的长度显然是比最短路要长的，于是答案一定为存在。

那么我们只需要跑上述算法就能很轻松的判定答案了。

正解：

实际上正解就很简单了， $1 \to n$ 的路径上经过了若干个点双，那么只需要分别判定这几个点双之间是否存在大于最短路的路径即可。为了便于实现，可以加一条 $(1, n, dis (1, n))$ 的边，这样 $1, n$ 就一定在同一个点双内了，这样就可以直接跑上述算法了。

P6790 [SNOI2020] 生成树

求一个仙人掌图上加一条边的图的生成树个数。

可以发现，这张图是广义串并联图，那么也就是说最后可以缩成一个点。

那么仍然考虑上述做法，设 $(f, g)$ 表示连通与不连通的方案数，那么：

删一度点：那么这条边一定是要选的，把 $f$ 乘到答案上；
缩二度点：
- $f^{'} = f_{1} f_{2}$ ；
- $g^{'} = g_{1} f_{2} + g_{2} f_{1}$ ，没有 $g_{1} g_{2}$ 的原因是中间的点必须得和左右两个点其中一个连通。
叠合重边：
- $f^{'} = f_{1} g_{2} + f_{2} g_{1}$ ；
- $g^{'} = g_{1} g_{2}$ 。

直接做即可。

P9333 [JOISC 2023 Day2] Council

首先过程实际上是将两个人的选择删除。

直接令 $p = ⌊ \frac{n}{2} ⌋$ ，那么删除后能影响到的提案仅有和为 $p, p + 1$ ，大于 $p + 1$ 的一定通过，小于 $p$ 的一定不通过。

那么只考虑这两者，如果一个 $p$ 两个人中有一个人选择的它，那么它就会被减去，如果一个 $p + 1$ 两个人都选它也就会被减去，也就是说，我们设 $a_{i}$ 为 $i$ 选择的 $p + 1$ 的集合， $b_{i}$ 为 $i$ 选择的 $p$ 的集合，那么问题相当于对于每一个 $i$ ，求 $min_{j \neq i} {popcount (a_{i} and a_{j}) + popcount (b_{i} or b_{j})}$ 。

改下式子，有 $popcount (a_{i} and a_{j}) + popcount (b_{i} or b_{j}) = popcount (a_{i} and a_{j}) + popcount ((\neg b_{i}) and b_{j}) + popcount (b_{i})$ ，即 $popcount ((a_{i} + (\neg b_{i})) and (a_{j} + b_{j})) + popcount (b_{i})$ ，令前者 $x_{i}$ 后者 $y_{j}$ ，则现在问题变成了求 $min_{j \neq i} popcount (x_{i} and y_{j})$ 。 $min$ 仍然不好求，再反一下改成 $max$ ，即 $min_{j \neq i} popcount (x_{i} and y_{j}) = popcount (x_{i}) - max_{j \neq i} popcount (x_{i} and (\neg y_{j}))$ ，那这样我们问题就变成了，给定一个序列 $a_{i}$ ，多次询问求 $max_{j \neq i} popcount (x and a_{i})$ 。

考虑一个类 FWT 的过程，首先对于每个 $a_{i}$ ，将其所有子集标记，因为最后的答案一定是某个 $a_{i}$ 的子集，然后再将现在所有标记的了的值的超集与它取 $max$ 。由于这里取的是 $max$ ，所以最后贡献到的一定是 $and$ 的值，如果求 $min$ 那么比 $and$ 小的集合也会贡献，于是就错了。那么直接高位前后缀 $max$ 即可。由于还有 $i \neq j$ 的限制，所以维护一个最大一个次大就行了。复杂度 $O (m 2^{m} + n m)$ 。

2023.10.26

想起之前谁发的犇犇：

看到有人说“必须要努力了，于是开始了一天三道题的高强度训练”，虽然感觉他确实是认真说的但是还是忍不住想笑。

被攻击到了 /kk。但是我觉得一天做三道题真的很困难了啊，为什么会有卷怪能一天卷完一整个 ≥ *3000 的题单啊？？？？

P9330 [JOISC 2023 Day1] Festivals in JOI Kingdom 2

首先正确的贪心方法肯定是按照右端点从小往大选。

我们考虑先计算出所有最后答案正确的方案数，再容斥一步就是答案。总方案数为 $1$ 到 $2 n$ 内所有奇数的乘积，证明考虑倒序给每一个 $a_{i}$ 匹配一个 $b_{i}$ ，这样每个 $b_{i}$ 能插入的位置有 $1, 3, 5, 7, \dots$ 种。

然后考虑如何统计两种方法答案相同的方案。首先假贪心的答案在任意一个前缀内肯定答案不会超过真贪心，而且如果某一时刻假贪心答案小于真贪心且假贪心选的右边界比真贪心靠右，那么之后假贪心答案一定不可能等于真贪心，进一步发现当两个答案差大于等于 $2$ 之后也一定不可能。这意味着，从左往右依次加入后，两者答案差永远不超过 $1$ ，也就是说两者的区间一定是交替出现的。

那么按照这种思想，我们可以设计出一个弱智 DP，考虑 $f_{i, S, p, q}$ 表示当前填到 $i$ ，有集合 $S$ 中的左端点没有匹配右端点，且假贪心最后一个右端点为 $p$ ，真贪心右端点为 $q$ ，合法方案数。转移要不然加入 $S$ ，要不然从 $S$ 中选一个匹配，然后多讨论一下即可。

发现记录集合 $S$ 显然是弱智的，可以发现上述过程仅需要知道三个区间内的左端点各有多少，所以改成记录三个数即可做到 $O (n^{4})$ ，状态为 $f_{i, p, q, r, 0 / 1}$ ，表示由最右的两个端点分成的三个区间内左端点各有 $p, q, r$ 个且最后一个区间为假贪心 / 真贪心。

再仔细分析一下这个做法的转移可以优化到 $O (n^{3})$ ，可以拿 51 分，不过到这里就优化不下去了。发现重点在于这里提前决策了哪些地方要放左端点，导致记录这些左端点是非常麻烦的。我们考虑按照右端点依次填入，每次将一个右端点对应的左端点插入，也就是每次直接插入一个区间。

我们将真贪心选中的区间称为红区间，假贪心选中的区间称为蓝区间，若两者重合则称其为紫区间，其它的区间称为黑区间。那么，如果将所有区间右端点从小到大排序，那么一定是红蓝交替再加上若干黑区间。

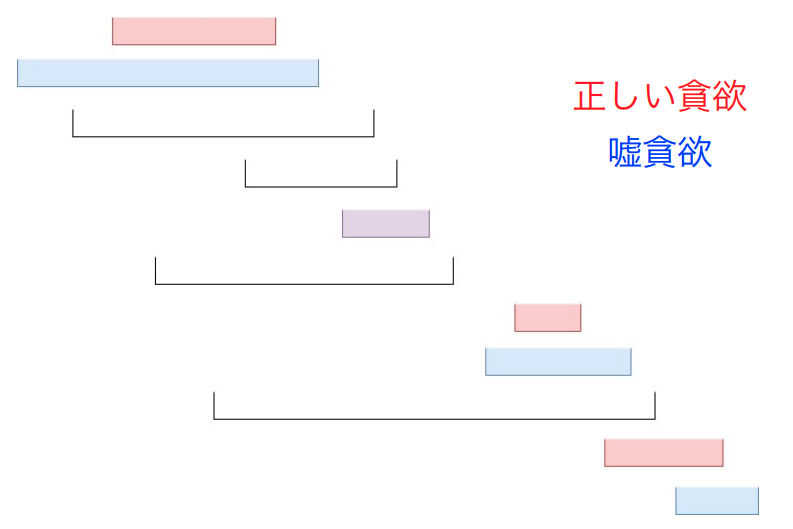
考虑再刻画一下合法的选择方案，对于红区间，两个相邻的红区间的右端点内不存在一个完整区间；对于蓝区间，两个相邻的蓝区间内不存在某个区间的左端点。

考虑这样一个插入顺序：每次插入一对区间与红区间到上一个红区间内的所有黑区间。对于所有黑区间，它们的左端点不能在某两个蓝区间的间隔内，这可以记录一下之前有多少非蓝区间内的间隔，然后用一个上升幂来计算。然后再计算一下黑区间与红蓝区间之间的顺序。这样就可以直接得到一个 $O (n^{3})$ 的做法了，状态 $O (n^{2})$ 转移 $O (n)$ 。需要对紫区间等单独讨论，具体需要记录一下最后一对区间是不是紫区间，然后根据两个区间的类别讨论转移。

继续优化就得考虑压缩状态了。注意到这里我们还单独记录了之前这些区间内有多少位置不是在蓝区间间隔内，这样的原因是左端点的选取限制很大。那么我们考虑倒着插入，这样左端点是枚举的而不是计数的。发现，此时右端点是可以插入到之前区间的任意一个间隙之间的。那么我们就只需要记录区间数，不需要再记录有哪些位置能插入了。

拿两端都不是紫区间的情况来举例子，假设当前考虑到 $f_{i, 0}$ ，枚举了有 $j$ 个黑区间，转移到 $f_{i + j + 2, 0}$ ，那么就有：

f_{i + j + 2, 0} \leftarrow f_{i + j + 2} + f_{i, 0} (j + 2) (j + 1) (2 i - 2)^{\overset{―}{j}}

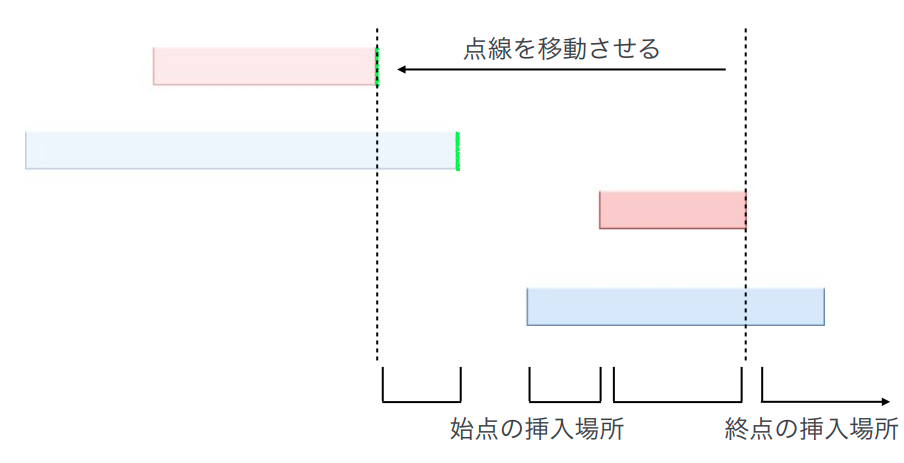
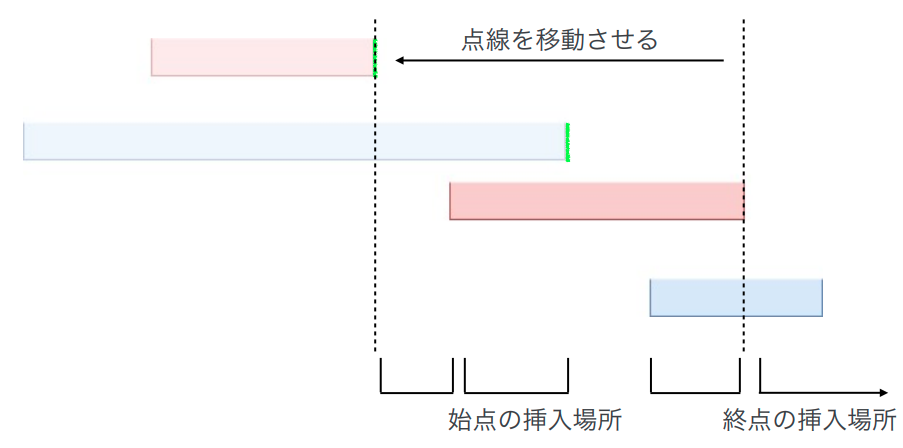
其中 $(j + 2) (j + 1)$ 是将黑区间左端点与蓝右端点、红左端点、蓝左端点混合的方案数，由于两个蓝端点中间不能有黑端点所以可以把这俩看做一个点，有 $j + 1$ 个空隙，所以方案数就是 $(j + 1)^{\overset{―}{2}}$ 。 $(2 i - 2)^{\overset{―}{j}}$ 就是在后面的空隙中选 $j$ 个。

那么直接这样转移即可做到 $O (n^{2})$ ，这样状态数是 $O (n)$ 的。

进一步分析，可以将上面的式子化简一下，发现是一个差卷积的形式，实际上是一个半在线差卷积，分治 NTT 即可，但是是任意模所以还得 MTT，但是你也可以跑 Karatsuba，但是狗都不写这些玩意，直接 $O (n^{2})$ 卡常就过了。

AGC020D Min Max Repetition

哇，我又啥都不会了！！！！！

首先考虑最大值最小是啥，肯定是让较少的一个作为较大的分隔符，假设 $a \geq b$ ，那么只需要满足 $⌈ \frac{b}{v} ⌉ \leq a + 1$ ，即 $v \geq ⌈ \frac{a}{b + 1} ⌉$ ，也就是说 $v$ 最小应该为 $⌊ \frac{a + b}{min (a, b) + 1} ⌋$ 。

考虑最优状态下，肯定是对于一个前缀为连续的 $v$ 个 $a$ 与一个 $b$ 更替，然后后缀为连续的 $v$ 个 $b$ 与一个 $a$ 更替，那么只需要找到这个分割点即可。

假设前面选了 $x$ 段 $a$ ，那么说明前面使用了 $x - 1$ 个 $b$ 用来分隔，且至少需要用 $(x - 1) v + 1$ 个 $a$ ，那么对于后缀来说就有 $a - (x - 1) v - 1$ 个 $a$ 与 $b - x + 1$ 个 $b$ ，设两者为 $p, q$ 。那么对于右面， $p$ 个 $a$ 最多可以分隔 $(p + 1) v$ 个 $b$ ，也就是说必须满足 $q \leq (p + 1) v$ 。首先如果 $v = 1$ 可以得知 $x$ 要不然是 $a$ 要不然是 $0$ ，因为最后的字符串一定是 $abababa$ 或 $bababab$ ，即要不然全是前缀要不然全是后缀。否则，整理不等式，可以得到 $x \leq \frac{v (a + v) - b - 1}{v^{2} - 1}$ ，而为了字典序最小，我们应该让 $a$ 的段数最大，那么 $x = ⌊ \frac{v (a + v) - b - 1}{v^{2} - 1} ⌋$ 。那么有了这点，我们就可以直接计算分割点了，有 $b$ 的数量为 $b - x + 1$ ，需要 $⌊ \frac{b - x}{v} ⌋$ 个 $a$ 隔开，于是分割点就是 $a + b - (b - x + 1) - ⌊ \frac{b - x}{v} ⌋$ ，然后输出方案是容易的，因为对于前缀来说等于 $b$ 的位置 $mod (v + 1) = 0$ ，后缀同理。

2023.10.27

哇，我昨天只做了两道题！！！！我效率太高了！！！！恼。

joisc 题都太可怕。

我宣布，perl 是强大语言！！！

print reverse($a=$/.<>)eq$a?Yes:No

P9339 [JOISC 2023 Day3] Cookies

假如箱子都固定了，那么我们有一个显然的贪心策略：按照箱子从大往小，每次填入个数最多的若干种曲奇，如果某一时刻没有这么多种曲奇就不合法，否则合法。

那么我们可以将题目的抽象为，令 $s = \sum a_{i}$ ，找到一个箱子大小序列 $d_{i}$ 满足 $\sum d_{i} = s, d_{i} \in B$ ，使得按照上述贪心策略不会出现曲奇不够的情况，最小化序列长度。

但是上述贪心仍然还是比较抽象，我们需要找到是否有解的充要条件来快速判断。设 $d_{i}$ 的序列长度为 $m$ ，根据 Gale-Ryser 定理，假设 $d_{i}$ 降序排序，那么上述问题的充要条件是 $\forall k \in [0, m], \sum_{i = 1}^{k} d_{i} \leq \sum_{i = 1}^{n} min {a_{i}, k}$ 。

证明

考虑上述问题可以建出一个网络流图，源点向左部点连 $d_{i}$ ，右部点向汇点连 $a_{i}$ ，左部点与右部点每一个点连 $1$ ，那么问题实际就是判断最大流是否等于 $s$ 。

由最小割最大流定理，我们要证即为最小割 $= s$ ，可以放缩一步改成证明最小割 $\geq s$ 。

考虑左部点不割 $S$ ，右部点不割 $T$ ，那么中间需要割的边的数量就是 $| S | | T |$ ，总花费就是 $2 s - \sum_{i \in S} d_{i} - \sum_{i \in T} a_{i} + | S | | T | = 2 s - \sum_{i \in S} d_{i} - \sum_{i \in T} (a_{i} - | S |)$ 。如果固定了 $S$ ，那么 $T$ 中的元素容易贪心选出最大值，即答案为 $2 s - \sum_{i \in S} d_{i} - \sum_{i = 1}^{n} max {a_{i} - | S |, 0}$ ，同时后面只跟 $| S |$ 有关系，所以前面肯定贪心选前 $| S |$ 大的点，设 $| S | = k$ ，那么最小割就是 ${min}_{p = 0}^{k} 2 s - \sum_{i = 1}^{k} d_{i} - \sum_{i = 1}^{n} max {a_{i} - k, 0}$ 。

如果最小割 $\geq s$ ，那么 $2 s - \sum_{i = 1}^{k} d_{i} - \sum_{i = 1}^{n} max {a_{i} - k, 0} \geq s$ ，即 $\sum_{i = 1}^{k} d_{i} \leq s - \sum_{i = 1}^{n} max {a_{i} - k, 0}$ ，由于 $\sum a_{i} = s$ ，那么 $\sum_{i = 1}^{k} d_{i} \leq - \sum_{i = 1}^{n} max {a_{i} - k - a_{i}, - a_{i}}$ ，即 $\forall k \in [0, m], \sum_{i = 1}^{k} d_{i} \leq \sum_{i = 1}^{n} min {a_{i}, k}$ ，这便是原问题的充要条件。

那么令 $c_{i} = \sum_{j = 1}^{n} min {a_{j}, i}$ ，我们就可以很简单的判定了，考虑直接设 DP $f_{k, i, s}$ 表示考虑了前 $k$ 大的 $b_{i}$ ，已经填入了 $i$ 个数，和是否能等于 $s$ ，那么有转移 $f_{k, i, s} \to f_{k + 1, i, s}$ 与 $f_{k, i, s} \to f_{k, i + 1, s + b_{k}} (s + b_{k} \leq c_{i + 1})$ 。直接转移即可 $O (n^{3})$ 。

考虑优化，首先发现由于当前选的数的最小值为 $b_{k}$ ，那么一定满足 $b_{k} i \leq s$ ，于是 $i \leq \frac{s}{b_{k}}$ ，调和级数总状态数实际上只有 $O (n^{2} \log n)$ 个，而显然这个 DP 是可以 bitset 优化的，所以上个 bitset 即可做到 $O (\frac{n^{2} \log n}{w})$ 了。

P9135 [THUPC 2023 初赛] 快速 LCM 变换

首先考虑进行这样的操作后整体的 LCM 会怎么变化。

先只考虑一个质因子，那么删除了两个数后，可以发现剩下的最大值一定是原来的最大值、次大值或次次大值，然后再与新的 $x + y$ 取 $max$ 。但是这看起来还是不是很可做。

注意到，如果 $p^{a} | x, p^{b} | y$ ，那么一定有 $p^{min (a, b)} | x + y$ ，也就是说，两者加入之后的幂一定大于等于其中幂的较小值，也就是说删除两个数之后最后的值仅有可能变成最大值、次大值或 $x + y$ 的幂，并且成为次大值一定是删除了最大值。实际上，我们还可以得到这还是充分条件，因为如果最大值有两个，那么最大值与次大值相等，我们不考虑这种情况，此时最大值仅有一个，那么有 $a \neq b$ ，可以证明， $x + y$ 的最大次幂一定等于 $p^{min (a, b)}$ ，假设 $a < b$ ，那么设 $x = p^{a} c, y = p^{b} d$ ，则 $x + y = p^{a} (c + p^{b - a} d)$ ，括号内的东西模 $p$ 不等于 $0$ ，所以 $p^{a}$ 就是最大次幂。也就是说如果删除的一个数是最大值，最后的最大值一定是原来的次大值，那么对于这种情况，我们的贡献就是：如果选择的两个数中有一个数为 $x$ ，那么给答案乘上一个常数。

如果删除的不是最大值，那么最后的最大值一定是原来的最大值与 $x + y$ 取 $max$ ，注意到此时贡献只与 $x + y$ 有关，那么我们可以把所有 $x + y$ 相等的对放在一起考虑，这样贡献就是一个常数了。那么我们只需要考虑所有 $x + y = d$ 的 $(x, y)$ 对与它们各自的贡献的乘积，这显然是可以一次卷积求得的，于是直接卷积即可。

2023.10.28

哇，我昨天又只做了两道题！！！！

CF1817E Half-sum

首先排序后，显然会选一个前缀为较小值，一个后缀为较大值。

然后就是怎么合并，前缀肯定要尽可能小，后缀肯定要尽可能大。把操作看成一棵树，那么实际上每个点的贡献系数就是 $\frac{1}{2^{d e p}}$ ，而一种合法的方案只需要满足贡献系数和为 $1$ 即可，证明可以归纳。那么考虑到找最小值，那么我们肯定是要让较大的值的系数较小，那么我们可以从小到大依次赋上 $\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \dots, \frac{1}{2^{n - 2}}, \frac{1}{2^{n - 2}}$ 。可以证明这样赋是最优的。

那么现在问题就变成了，找到一个分界点 $p$ ，最大化 $\sum_{i = p + 1}^{n} \frac{a_{i} - a_{i + 1}}{2^{n - i + 1}} - \sum_{i = 1}^{p} \frac{a_{i} - a_{i - 1}}{2^{i - 1}}$ 。

设 $b_{i} = a_{i} - a_{i - 1}$ ，显然有 $b_{i} \geq 0$ ，考虑当 $p \to p + 1$ 时，该式子的变化量 $Δ_{p} = \frac{b_{p + 2}}{2^{n - p - 1}} - \frac{b_{p + 1}}{2^{p}}$ 。显然，当 $b_{p + 1} = 0$ 时， $Δ_{p} \geq 0, Δ_{p - 1} \leq 0$ ，那么说明此时选 $p$ 一定不如选 $p + 1$ 或 $p - 1$ 优，也就是说当 $a_{p} = a_{p + 1}$ 时选 $p$ 为分界点一定是不优的。所以我们选择的点一定满足 $a_{p} \neq a_{p + 1}$ 。

考虑 $p \to q$ 的变化量 $Δ = \sum_{i = p}^{q - 1} Δ_{i}$ ，可以得到：

Δ = - \frac{b_{p + 1}}{2^{p}} + \sum_{i = p + 1}^{q - 1} (\frac{1}{2^{n - i}} - \frac{1}{2^{i}}) b_{i + 1} + \frac{b_{q + 1}}{2^{n - q}}

假设 $p < q \leq \frac{n}{2}$ ，那么发现此时 $(\frac{1}{2^{n - i}} - \frac{1}{2^{i}})$ 一定恒小于 $0$ ，那么如果此时 $\frac{b_{p + 1}}{2^{p}} > \frac{b_{q + 1}}{2^{n - q}}$ ，那么此时 $Δ < 0$ ，即将 $p$ 换成 $q$ 是不优的。注意到，由于 $b_{p + 1} > 0$ ，那么如果 $n - q - p \geq 30$ 时，这个不等式一定成立，因为 $b_{i} \leq 10^{9}$ ，于是若 $p \leq \frac{n}{2} - 30$ ，那么就一定有 $n - q - p \geq 30$ ，也就是说任意 $q$ 都不会比 $p$ 更优。那么我们只需要找到第一个 $b_{p + 1} > 0$ 的位置 $p$ ，如果 $p \leq \frac{n}{2}$ ，那么此时 $p$ 就是左半部分的最优决策点。否则，左半部分最优决策点仅出现在 $(\frac{n}{2} - 30, \frac{n}{2}]$ 区间内，这部分的点数也是很少的，所以可以直接把所有可能的决策点拿出来跑一遍。右半部分同理，于是这样我们仅有 $O (\log V)$ 个可能的决策点，只需要对这些点均 check 一遍即可。check 需要高精，所以总复杂度 $O (n \log V)$ 。

有另外一种做法：考虑到对于两个决策点 $p, q$ ，孰优孰劣仅取决于 $[p, q]$ 内的 $a_{i}$ 值，外面的值的系数是完全相等的。于是，我们可以求出在一个区间内的最优决策点，那么我们可以分治，每次找出左右两个区间内的最优决策点后，判断两个决策点哪个更优，复杂度 $O (n \log n)$ 。维护大数需要使用 Trygub Number。

P8424 [JOI Open 2022] 跷跷板（Seesaw）

首先有一个显然的性质：删左边会使重心右移，删右边会使重心左移。

给出一个区间，判定合法是容易的，只需要能往哪走就往哪走即可，容易证明这种做法是对的。而由此我们可以推出更简洁的结论：只要对于每一个长度，存在一个区间的重心在给定区间内，那么这个区间就一定是合法的。这个也是容易证明的。

那么，我们的问题就变成了，选择一个区间，使得区间包含每一个点集中的至少一个点。注意到这个区间必须包含最一开始的重心，那么意味着对于每一个点集内，只有一开始重心左边的第一个与右边的第一个点是有用的，如果包含了更靠左或更靠右的点那么一定包含这个点，所以我们只需要考虑这些点即可。

那么就是个很简单的问题了，找出一个最小的区间使得满足 $n$ 个条件，要不然包含 $a$ 要不然包含 $b$ ，直接按照 $a$ 排序然后对每一种选择方案扫一遍即可。

AGC017E Jigsaw

发现一定是一个 $d = 0$ 的与一个 $c \neq 0$ 或一个 $d \neq 0$ 与 $c = 0$ 的相连，那么考虑建一张图，分为黑点和白点，黑点为 $c = 0 / d \neq 0$ ，白点为 $d = 0 / c \neq 0$ ，那么每一个拼图就可以看做这张图上的一条边，一种连接方案可以看做一条连续的链。这样问题就转化成了在这张图上找若干条从黑点到白点的路径覆盖，这可以看做是连若干条从白点到黑点的边，使得整张图有一条从黑点到白点的欧拉路径，那么令点的权值等于出度减入度，每次操作相当于会使得一个黑点权值 $- 1$ ，白点权值 $+ 1$ ，那么只需要满足黑点权值没有负数，白点权值没有正数即可。注意不能存在一个连通块内权值全为 $0$ ，否则这时候得到的是欧拉回路，无法变成从黑点到白点的路径。

2023.10.29

再次宣告 perl 胜利！！！

$_=<>;print-/(.)/+s/$1//g

AGC018F Two Trees

哦哦哦哦哦哦。

首先注意到一个点所填的数的奇偶性一定与其儿子个数相反，那么说明如果两个点的儿子个数奇偶性不相等则一定无解。

考虑一个神秘的转化：将点权变成给边定向，定义入度为正出度为负，发现，如果令每个点的出度入度之和为 $0$ ，那么一个点向父亲的连边的方向恰好就是子树和。那么我们就可以考虑构造一张欧拉图，将两个树的根连向一个超级根，然后将所有度数为奇数的点之间连一条边。这样，令偶数度数点的权值为 $0$ ，奇数度数的点的权值与连的边的方向一致（ $\pm 1$ ），显然这张图是有欧拉回路的，那么随便找一条欧拉回路，就能构造出一种方案了。

UOJ821 【UR #26】石子合并

人生中打的第一场 UR，因为 T1 预处理少了阶乘喜提 30 分，成功掉分，哦哦哦哦哦哦哦哦哦哦哦。

考虑这样一件事情：如果一个数后面有严格比他小的数，那么这些严格比他小的数一定和这个数在同一个序列中相邻出现，因为如果某一时刻选择了这一段的开头，那么说明这一段的开头是比另一个数组的开头元素小的，而后面的数均严格比它小，也就是说接下来一定会把后面严格比他小的数全部选上。于是我们可以将所有严格比前面小的数删去，显然答案是不变的。

这样我们就只考虑 $a_{i} \leq a_{i + 1}$ 的情况了。发现，如果数字互不相同，我们等价于将 $m$ 个数划分成 $n$ 个集合，发现这就是个斯特林数。但是如果你直接写了会发现第三个样例就 WA 了，因为存在相同的数的时候这几个数并不能随意放到集合内。具体来讲，你发现这几个数之间是没有相对顺序关系的，而直接任意放集合会给它们加上一个顺序关系，所以就多算了。那么考虑类似于斯特林数的求法，直接二项式反演求至多放了多少个集合的方案数，那么就可以直接组合数计算了，大概是一个 $\sum_{i = 0}^{n} (- 1)^{n - i} (\binom{n}{i}) \prod_{j = 1}^{t} (\binom{c_{j} + i - 1}{i - 1})$ ，其中 $t$ 为不同的数的个数， $c_{j}$ 为每个数的出现次数。直接实现就是 $O (n m)$ 的。

考虑快速计算出后面那个式子。首先比较无脑的做法就是发现后面是关于 $i$ 的 $m$ 次多项式，暴力分治乘出来然后跑多点求值。当然我不会写多点求值所以我们肯定不写这个。注意到， $\sum c_{i} = m$ ，所以我们可以考虑根号分治，对于 $\leq B$ 的 $c_{i}$ 我们统计各出现了多少次，然后枚举值域快速幂计算，对于 $> B$ 的 $c_{i}$ 不会超过 $\frac{n}{B}$ 个，这些数直接暴力计算，于是我们就有了一个显然的 $O (n \sqrt{m \log m})$ 的做法。

实际上你发现前面快速幂的 $\log$ 感觉上根本卡不满，事实上精细的分析可以得到前面一部分的复杂度是 $O (B)$ 的，具体证明看官方题解。所以我们就以 $O (n \sqrt{m})$ 或 $O (m \log^{2} m)$ 的复杂度内解决了本题。

2023.10.30

恼了，这下彻底不可能完成 10 月 to-do list 了。最后写两天，11 月开始打模拟赛了。

CF1148F Foo Fighters

题目给的限制很诡异，我们转化一下。出现奇数次可以让我们联想到异或，假如我们令 $S_{i}$ 为二进制位有第 $i$ 位的集合，不难发现如果选择的某个数 $s$ ，实际上就是让对应的若干个 $S_{i}$ 的集合的对称差全部取负。那么，我们现在的问题变成，选择若干个集合，使得这些集合的对称差的和大于等于总和的一半。

考虑从前往后求出每一个数的第一次出现位置。接下来倒着扫一遍，注意到，当扫到某个数为这个数的第一次出现位置后，这个数在后面就永远不会出现了，那么我们可以对每一个这样的第一次出现的数的集合考虑，如果当前选中的集合中的数不超过一半，那么就选择当前的集合，这样会使得第一次出现的集合取反，就一定超过一半了，直接这样构造即可使得总和超过一半。

P9069 [Ynoi Easy Round 2022] 堕天作战 TEST_98

倍增值域分块板子。

发现如果小于 $x$ 的数被减完后就小于 $0$ 了，之后任意操作都会影响到这些数，所以可以直接单独一个线段树维护它。然后就是一个经典问题，区间 $> x$ 的数 $- x$ 。考虑倍增值域分块，将值域划分成 $[b^{i}, b^{i + 1})$ 的 $\log_{b} V$ 个区间，对每个区间维护线段树。注意到，如果 $x < b_{i}$ ，那么会对整个区间内的所有数减 $x$ ，可以维护最小值并找到所有 $< b^{i}$ 了值，将它们放到值域更小的线段树内去。如果 $x \in [b^{i}, b^{i + 1})$ ，可以发现，如果这里面的数减少了 $x$ ，那么这个数在 $O (b)$ 次操作后就一定会到值域更小的区间内，于是发现每个数实际上只会被减 $O (b \log_{b} V)$ 次，那么上述算法复杂度就是均摊 $O (n b \log n \log b)$ 的。理论上取 $b = 2 / 4$ 最优，实际上把 $b$ 开的很大，大约到 $16$ 才能跑过去。

哦这玩意其实就是 P7447 [Ynoi2007] rgxsxrs，lxl 讲课的时候讲的这个，但是这题好像还需要 $O (n)$ 空间，所以摆了。

P9597 [JOI Open 2018] 猫或狗

设 $f_{u, 0 / 1 / 2}$ 表示 $u$ 子树内， $u$ 所在连通块没有出现宠物 / 出现猫 / 出现狗，那么有转移：

{\begin{cases} f_{u, 0} = \sum f_{v, 0} \\ f_{u, 1} = \sum min {f_{v, 1}, f_{v, 0}, f_{v, 2} + 1} \\ f_{u, 2} = \sum min {f_{v, 2}, f_{v, 0}, f_{v, 1} + 1} \end{cases}

然后直接套个动态 DP 就完了。

P7564 [JOISC 2021 Day3] ボディーガード

~~传统艺能：还没写题解但是先口胡一下并且把题解放在这里以显示自己看起来一天做了挺多道题的假象。~~

首先可以将题目画到一个二维平面上，横坐标为位置纵坐标为时间，那么每个人就是平面上一段斜率为 $\pm 1$ 的线段，询问变为每次给定一个点，询问从这个点向左上或右上移动，路径与所有线段重合的距离乘权值之和。

发现所有过程都是斜着的，我们把坐标系旋转一下，这样就变成了每次向右或向上移动，有若干条横纵线段。发现，这些线段组成的格点共 $O (n^{2})$ 个，我们可以先 DP 一遍求出从每个格点出发的最大权值。

那么现在考虑如何查询。对于任意一个点，它的路径肯定是到达某个格点然后再加上格点的权值，容易发现肯定是先一直往上走，然后在某个格线往右走到格点，或先向右走然后沿格线向上。两者取 $max$ 即可，我们现在仅考虑向上走。

我们将所有在同一个竖列中的询问拿出来考虑，发现，每一条格线的贡献是一个关于询问点的横坐标到格线右端点的距离的一次函数，设这个距离为 $x$ ，那么贡献显然为 $c_{i} x + v a l$ 。每次询问时考虑的是一个前缀的一次函数，那么直接拿李超树维护就能 $O (n^{2} \log n + q \log n)$ 了。不是特别优秀，我们继续优化。

注意到，从上往下的 $v a l$ 值肯定是单调递增的，也就是说一次函数的截距是单调递增的，那么如果之前有一个一次函数斜率小于它那么它肯定是不优的，于是可以单调栈维护出这个函数，然后查询二分即可，复杂度 $O (n^{2} + q \log n)$ 。

2023.10.31

恼了，十月做不完十月 to-do list 了。摆烂了，就这样了，明天开始打模拟赛了，要不然 NOIP 再打不好就真退役了。

CF1491F Magnets

妈了我真傻逼。想了一堆无意义东西，然后正解极其简单。

考虑从前往后扫，每次查询 $i$ 与 $[1, i)$ 之间的贡献。容易发现，第一次贡献不等于 $0$ 的时候就是出现第二块磁铁的时候，我们知道一块磁铁之后后面哪些是磁铁就容易确定了，第一块二分一下即可。

CF1427F Boring Card Game

首先考虑如果不管交替的限制，任意顺序加入，那么显然可以用一个栈来维护。

那么，用栈求出一组方案后，我们可以将栈的限制建成一个森林，在选一个点之前必须把其子树全部选完。同时每个点用颜色表示这个点应该先手还是后手选择，先手白点后手黑点。那么现在问题就是，对于给定的一个森林，能否按照拓扑序交替选择黑白点选完所有点。

注意到，白点黑点数量相同，且最后一个点选取的点一定是黑点。那么也就是说，至少有一棵树的根为黑点。于是我们有一个贪心：

先手任意选一个叶子；
后手优先选一个非根的叶子，若没有非根叶子则选取一个根。

可以证明上述过程一定可以将所有点选完。具体考虑：

由于一定存在一棵树的根为黑点，那么考虑如果所有叶子都是黑点，那么每个白点一定有一个儿子为黑点，说明白点数一定小于黑点数，而存在一个黑根不与一个白点对应，说明黑点一定大于白点，与黑白点数量相同矛盾；
后手选择的时候，黑点数等于白点数加一，可以用类似的方法证明一定存在一个黑叶子，且不可能仅有一个叶子为最后一个黑根。

于是直接做即可。

2023.10 完结 🎉

Happy Halloween!

posted @ 2023-10-25 21:36 APJifengc 阅读(445) 评论(3) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 2024.1 训练纪要

· NOI 2024 前做题纪要

· Before NOIP2021

· 2023 年 7 月训练记录

· 2024.12.12 近期练习

阅读排行：
· 10年+ .NET Coder 心语 ── 封装的思维：从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源！
· 周边上新：园子的第一款马克杯温暖上架

apjifengc's blog

2023.10 做题纪要 #3