2023.9 做题纪要 #2
2023.9.14
哇哦,居然出现了第二篇博客。
前两天 whk,顺便感了个冒,所以 whk 也没咋看。今天还没完全恢复,浅更一下吧。
先把 AGC 优先级调低点,天天做 AGC 好像也不是很好。
做点数据结构吧,ds 好啊(
P3920 [WC2014] 紫荆花之恋
其实是待办事项放了好久的东西。简单练练码力。
我们每次加入一个点,所以只需要考虑这个点与其它哪些点能够造成贡献即可。题目要求点对贡献且与距离有关,这显然是点分树能够解决的问题,设 \(dis(u)\) 为 \(u\) 到分治中心的距离,那么条件就是 \(dis(u) + dis(v) \ge r_u + r_v\),即 \(r_v - dis(v) \le dis(u) - r_u\)。那么我们只需要用平衡树维护 \(r_v - dis(v)\),查询只需要知道有多少数小于等于 \(dis(u) - r_u\) 即可。
难点在于题目强制在线,我们不能直接建点分树。可以每次直接在点分树下拓展,然后类似于替罪羊树的方法进行大力重构即可。
难点在实现。
CF1408H Rainbow Triples
假如我们将最后选择的方案看做若干个区间,那么是存在一种方案使得所有区间都有交的,因为如果两个区间无交交换两个端点一定是合法的。而这样我们可以使得所有选择的区间全部尽量靠左和靠右,于是一定存在一种方案使得选择的 \(0\) 是一个前缀加一个后缀。
设一共有 \(m\) 个 \(0\),那么每个区间的左端点一定在 \([1, \lfloor m/2 \rfloor]\) 个 \(0\) 中,右端点一定在 \([\lceil m/2 \rceil, m]\) 中。考虑从中间划分开这个序列,那么对于左边的数,我们只需要考虑左边能否匹配上一个 \(0\),因为右边无论如何都能找到一个进行匹配。同理右边的数只需要考虑在右边找一个 \(0\) 进行匹配。于是,我们将问题转化成了一个类似于二分图的问题,每个颜色可以选择一个数,从一个前缀或一个后缀中选择一个数进行匹配。这非常网络流,所以我们可以建一个网络流模型出来。
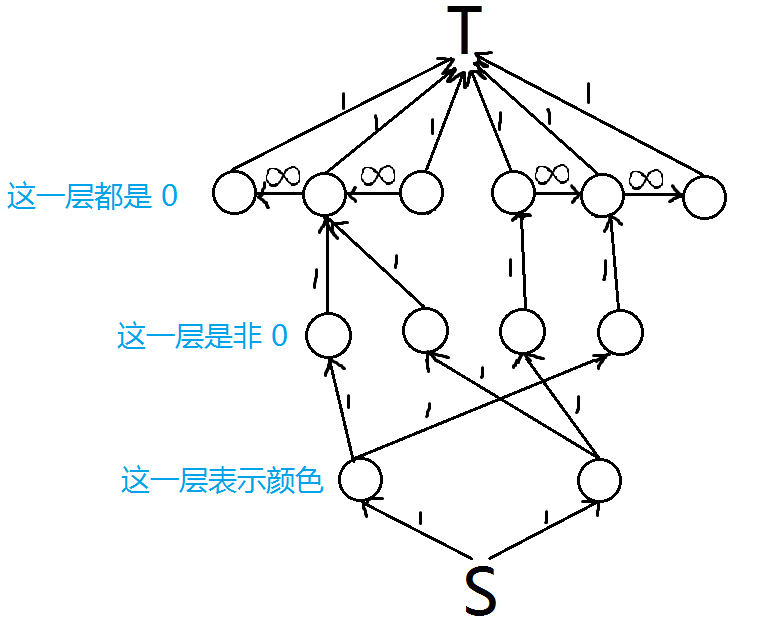
(复制了一张图)
考虑最大流等于最小割,每个颜色要不然将上面的前缀后缀边全部割掉,要不然割源点向颜色点连的一条边。考虑枚举割的前缀后缀的边,那么如果某个颜色没有全部被割那么就要割下面的边。这个过程是容易线段树维护的。
2023.9.15
昨天有点摆。虽然今天应该不会有任何改进。
嗓子还是疼,感冒真 nm 难受。寄。
上午一直在水,哈哈。看了眼初赛,SoyTony 将不定积分的总习题课做完了,膜拜。我只会积最简单的,我好弱。
然后下午更水了。算了我水吧。
CF1534G A New Beginning
挺简单的题其实是,不过我把贡献函数看成曼哈顿距离了然后想了半天不会,非常弱智。
考虑到贡献是一个形如正方形的东西,那么我们在正方形的左上角或右下角进行操作一定不劣,也就是在斜率 \(-1\) 的直线上进行操作。按照截距排序后,问题变为:
每次可以将 \(x\) 加 \([0, a]\) 中的任意数,并将 \(|x-b|\) 贡献到答案上。
这个显然是可以 DP 的,而且贡献函数是绝对值函数,直接上 Slope Trick。前面的操作可以看做一个区间取 \(\min\),凸函数进行这个操作发现就相当于从斜率为 \(0\) 处断开,右半部分向右平移一段距离。那么我们分开维护左右两部分即可,打一个 tag 维护。
CF1696G Fishingprince Plays With Array Again
好题啊好题啊好题啊好题啊好题啊好题啊好题,一开始想线性规划了但是感觉应该不会有太大关系,然后想贪心去了,然后结果还真就线性规划。
以下默认 \(X < Y\)。
题目给出的限制很容易写成线性规划的形式。设 \(x_i\) 为在 \(i\) 处操作 \((+X, +Y)\) 的次数,\(y_i\) 为在 \(i\) 处操作 \((+Y, +X)\) 的次数,那么容易写出线性规划的问题:
欲最小化 \(\sum_{i=1}^{n - 1} x_i + y_i\),满足:
- \(X(x_i + y_{i-1}) + Y(x_{i-1}+y_i) \ge a_i\);
- \(x_i, y_i \ge 0\)。
考虑其对偶问题,可以画一个系数矩阵出来,容易发现其对偶为:
欲最大化 \(\sum_{i=1}^n a_i z_i\),满足:
- \(X z_i + Y z_{i+1} \le 1\);
- \(Y z_i + X z_{i+1} \le 1\);
- \(z_i \ge 0\)
发现这个问题的形式优美了极多,而且变量之间的限制也少了很多。此时我们若直接记录上一个 \(z_i\) 选的什么,那么就可以直接 DP 了。但是显然没法直接记录。
众所周知线性规划可能取到的点一定是某个交点,那么考虑将上述问题画在二位坐标系上考虑。发现三个交点分别是 \((0, \frac{1}{Y}), (\frac{1}{X+Y}, \frac{1}{X+Y}), (\frac{1}{Y}, 0)\)。发现所有交点实际上只会出现三个坐标 \(0, \frac{1}{X+Y}, \frac{1}{Y}\)。这样我们就将值域减少到了 \(3\)。然后就很容易直接 \(O(n)\) 进行 DP 求解了。
考虑区间查询,这个东西容易写成 max-add 矩阵的形式,直接线段树维护矩阵即可。
2023.9.16
今天下午初赛,名正言顺摆了。
ABC320G Slot Strategy 2 (Hard)
好像摆一整天也不合适,所以晚上 ABC 看了个 G。
有一个很直接的想法:直接枚举最后的数是啥,然后二分答案,这样实际上就是一个二分图匹配的问题,暴力跑。但是这样复杂度太高了,而且答案并不能给出一个合理的上界。
考虑减少一些。可以发现,如果每个点连出的边足够多了,那么剩下的可以直接不考虑。二分答案实际上在找有没有完美匹配,考虑 Hall 定理,只要邻居大小大于等于左部点集合大小就好,而左部点集合大小最大也就是 \(n\),那么我们对于每个点,只连前 \(n\) 条边就一定存在完美匹配了。这样待选的最后答案就只有 \(O(n^2)\) 个了,直接暴力跑网络流或者匈牙利复杂度就是 \(O(\omega n^3 \log n)\) 的(\(\omega = 10\)),可以通过。
2023.9.17
今天下午放假,名正言顺摆了。
CF1726G A Certain Magical Party
考虑分析一些性质。首先设最后得到的数为 \(T\),那么显然 \(T\) 是大于等于最大值的。那么考虑每个数能够得到的快乐值。如果这个数属性为 \(0\),那么发现他能增加的就是有多少小于它的数出现在它后面,因为出现在前面会使得它变成 \(T\),一定大于它。同理,属性为 \(1\) 增加的就是有多少数大于它,或小于等于它,且出现在它前面。
首先可以证明,如果有解,不可能存在两个 \((x, 1)\)(\(x < T\))。如果有的话,较前的一个一定会大于较后的一个值,使得较后的一个值增长的数比他大,则不可能相等。
我们首先将最大值等于最小值的情况特判掉。那么设最小值为 \(m\),发现,最小值 \(m\) 的属性肯定不能是 \(0\),否则一定无解,而如果是 \(1\),由于没有与它相同的数,那么它增加的一定是 \(n-1\),于是可以得知 \(T = m + n - 1\)。
然后我们就可以计算方案数了。首先所有 \((T, 1)\) 是可以随意排列的,然后从小到大考虑每个 \((x, 0), (x, 1)\)。对于一个 \((x, 0)\),小于它的数中需要恰好有 \(T - x\) 个数在它后面,对于一个 \((x, 1)\),小于等于它的数中需要恰好有 \(x - m\) 个数在它后面。那么发现每个数能填的位置就固定住了,只有多个 \((x, 0)\) 之间的顺序可以改变,所以只需要将这些阶乘乘起来就是方案数。
2023.9.18
即使放假做题纪要也不断更,这就是衡中带给我的自信!!111
昨天下午放假今天下午返校,开心。
但是好像今天确实啥都没做。
CF1491H Yuezheng Ling and Dynamic Tree
好像是很简单的,但是没想到分块也没想到分块维护啥,我好弱。想到维护啥之后好像这题就做完了。
考虑一个类似于 P3203 [HNOI2010]弹飞绵羊 的做法,维护每个块能够到达的下一个块的最靠后的节点 \(b_i\)。那么发现求 LCA 可以类似于树剖 LCA 的做法每次跳一整个块,能够到达的下一个块的位置相同后再暴力跳父亲,复杂度就是 \(O(\sqrt{n})\) 的。考虑维护,散块直接暴力重构,但是整块似乎不好维护。但是发现一个整块进行 \(O(\sqrt{n})\) 次操作后所有的 \(b_i\) 一定都小于 \(i\) 所在块的左端点,也就是之后的所有操作对 \(b_i\) 的操作一定是区间减,那么前 \(\sqrt{n}\) 次整块操作暴力,然后维护一个 tag 即可,总复杂度 \(O(n \sqrt{n})\)。
2023.9.19
困困困困困困困困困困困困困困困困困困困困困困困困。
急需一个能够晚上抱着睡觉的东西,有没有好心人 v 我一个(
CF1801G A task for substrings
然而我还是不会串。感觉要加训串了。
感觉好尴尬啊,到现在为止这个做题纪要里面没有一道题是我自己想出来的,呃呃。
首先这个问题就很 AC 自动机,实际上就是在求 AC 自动机上一条路径的权值和。
考虑差分,用 \([1, r]\) 减去 \([1, l - 1]\) 再减去所有左端点在 \([1, l - 1]\),右端点在 \([l, r]\) 中的串。前两个是很容易求的,扫一遍就能预处理出答案,重点在后者。
后者实际上是在找经过一个分割点的串有多少,可以将经过的串看做一个前缀加一个后缀拼成的,那么相当于对于 \(T[1, l - 1]\) 的所有后缀与 \(T[l, r]\) 中的所有前缀,有多少对能够拼成一个子串。首先这样的合法串对是 \(O(\sum |s_i|)\) 的,然后前缀后缀关系可以通过建失配树转化成树上关系,然后就变成了一个矩形加单点求值的问题了。所以我们可以对 \(|s_i|\) 建一个正 AC 自动机与反 AC 自动机(分别对应所有的前缀与所有的后缀),然后找 \(T[l, r]\) 对应的节点可以倍增。
CF1458F Range Diameter Sum
感觉非常强大啊。只知道直径能合并,没见过还能这样合并。
首先介绍“树上邻域理论”或“树上圆理论”。类比平面上的圆,我们可以将树上一个点集用其“最小覆盖圆”表示,即用其重心与半径(直径的一半)来表示。
为了防止存在两个重心的情况,我们将每条边的中间加一个点,这样所有的重心一定在某个点上。我们记一个邻域为 \(C = (c, r)\),其中 \(c\) 为重心,\(r\) 为半径。
发现,这个东西与圆的很多性质是相同的,其中包括两个圆的合并。
具体来讲,如果 \(C_1 \subseteq C_2\),则并为 \(C_2\),\(C_2 \subseteq C_1\) 并为 \(C_1\),否则并为 \((\mathrm{go}(c_1, c_2, \frac{1}{2}(\mathrm{dis}(c_1, c_2) - r_1 + r_2)), \frac{1}{2}(\mathrm{dis}(c_1, c_2) + r_1 + r_2))\)。原因画个图易知。(\(\mathrm{go}(u, v, d)\) 表示 \(u\) 向 \(v\) 走 \(d\) 距离的位置)
若 \(C_1 \subseteq C_2\),则有 \(\mathrm{dis}(c_1, c_2) + r_1 \le r_2\),这样我们就很容易判定两个邻域是否有包含关系了,也很容易计算两个邻域的并。
以上所有具体证明咕了。
于是发现两个直径合并可以用式子表示了,而不是传统合并的直接枚举两个端点。
回到这题,容易想到分治计算,然后发现此时问题就是要求两个集合中所有邻域对的并的半径和。(因为中间加个个点,所以原来的直径等于现在的半径)
直接固定左边选的邻域 \(C_1\),考虑右边的所有邻域与左边的关系。发现,一定是先有一部分 \(C_2 \subseteq C_1\),然后是互不包含,然后是 \(C_1 \subseteq C_2\)。原因是右边的邻域只会扩大,每一个邻域都是包含前一个邻域的,所以存在单调性。同时,如果左边选的圆扩大,右边的圆的两个分界点都会单调向右移动。
那么,我们直接指针维护两个分界点,然后就能方便计算答案了。其中第二种情况要计算一个形如 \(\sum_{v\in S} \mathrm{dis}(u, v)\) 的东西,这个容易用点分树维护出来。由于两个指针都是单调的,所以连可持久化啥的都不用写,直接修改即可。
2023.9.20
SoyTony: 你把 Sonnety 的 fufu 抢过来。

cf 的举报机制是什么样的啊,怎么今天突然给我蹦出来一个举报按钮。


久违的比赛日。
我想上 3 Dan。我想上 3 Dan。我想上 3 Dan。算了 perf 2800 我感觉我都做不到。
CF 反正是打不动了,perf 稳定不了 2400+,是不是彩笔啊。而且熬不了夜,CF 比赛全打不了。
CF1637H Minimize Inversions Number
这题好牛。一步也想不到。
首先有一个性质:存在一种最优的选择方案,如果 \(i\) 被选中了,那么所有 \(j>i,p_j < p_i\) 的数全部也被选中。
考虑将这个东西画成图,二维平面上 \(n\) 个点 \((i, p_i)\)。假设有两个点 \(i, j\) 满足 \(j>i,p_j < p_i\),此时 \(i\) 选中而 \(j\) 未选中,那么考虑将 \(i\) 换成 \(j\) 造成的贡献。我们定义一个点的贡献为交换后它形成的逆序对的减少两,分类讨论一下可以得到下图:
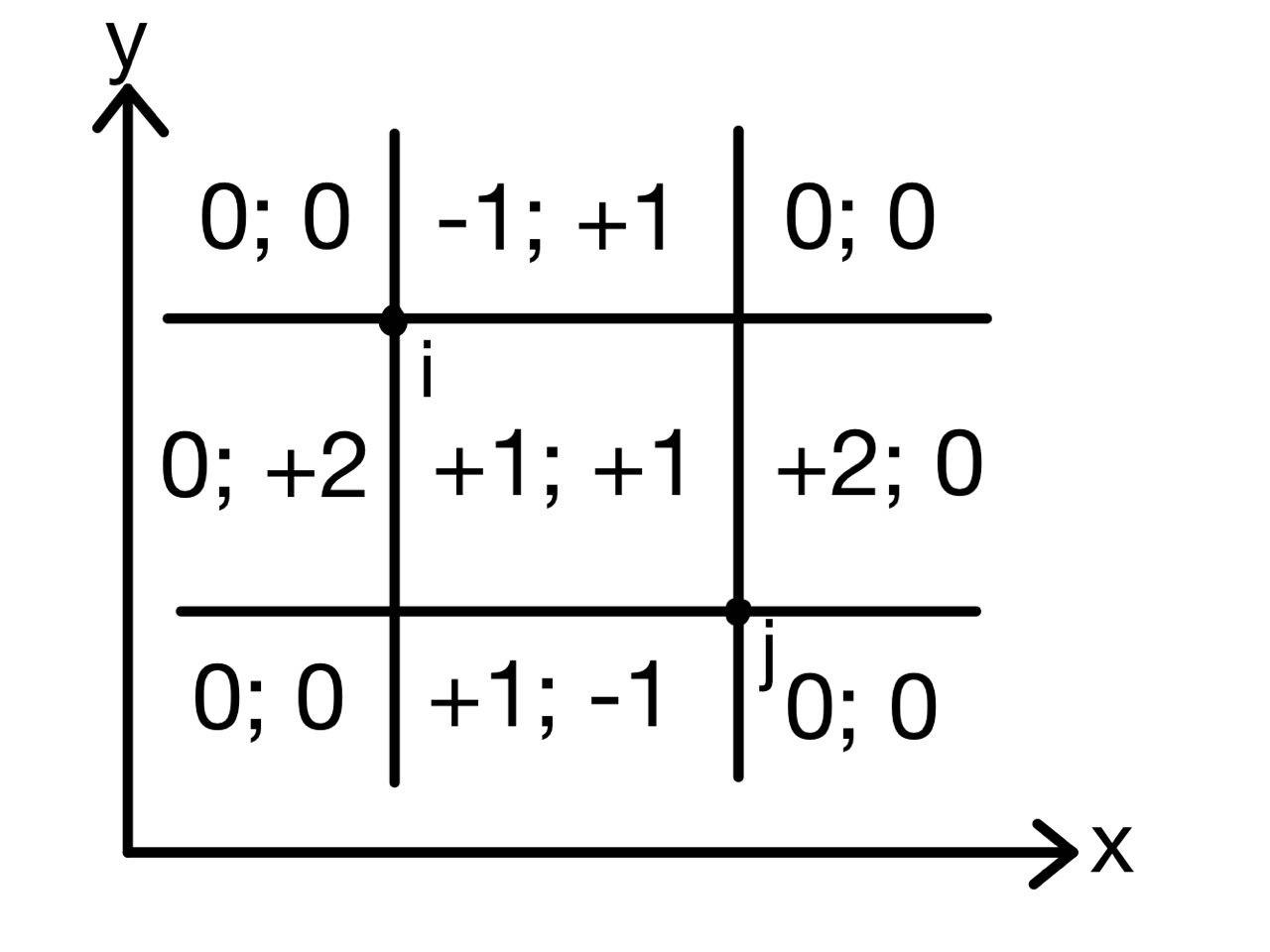
每个格子中第一个数表示选中的点的贡献,第二个表示没选中的点的贡献。
发现只有两种情况贡献是负数:在上面选中与在下面未选中。而发现如果存在这两种情况之一,我们可以选择这个数得到一对新的 \((i, j)\),重复这个过程一定能找到一对 \((i, j)\) 满足不存在负贡献,那么说明如果存在这种情况一定可以通过更改选中状态使得逆序对数量不增。
接下来考虑写出选中集合 \(S\) 时逆序对数的表达式。设 \(inv\) 为原序列的逆序对数。考虑操作后逆序对减少了哪些,发现仅有 \(i < j\),\(i\) 未选择且 \(j\) 选择了的点对造成贡献,那么具体而言就是:
(记号有点混乱,反正 \(\#\{[1, i) \not \in S < p_i\}\) 就是 \([1, i)\) 中不属于 \(S\) 的值中 \(< p_i\) 的数量,其它的类比一下)
\(\#\{[1, i) \not \in S < p_i\} = \#\{[1, n] \not \in S < p_i\}\):因为 \(\#\{(i, n] \not \in S < p_i\} = 0\),这是根据最优解下不存在 \(i < j, p_i >p_j, i \in S, j \not \in S\) 得出的。
反正最后能够得到一个非常优美的形式:设 \(c_i = 2p_i - i - 1\),那么答案就等于 \(inv + \sum_{i \in S} c_i - \frac{|S| (|S| - 1)}{2}\)。而又注意到,如果有 \(i < j, p_i > p_j\),那么 \(c_i > c_j\),这意味着我们按照 \(c_i\) 的值从小往大选就能够满足最一开始推的最优解的限制,而这同时也是逆序对最小值,于是我们只需要给 \(c_i\) 排个序就做完了。代码极短。
CF1750G Doping
大力组合意义加暴力优化,赢!
不过最开始我推的方向都是错的,傻逼了,没想到最后一起容斥。
考虑没有字典序的限制怎么做。显然是一个容斥的状物,考虑钦定划分了哪些段,然后再钦定一些段是连续的进行容斥。
但是每次计算都容斥一遍非常不优,考虑和到一起最后容斥。具体的,设 \(g_k\) 表示将序列划分成 \(k\) 段的方案数(不需要是最少),那么容易有 \(g_k = \sum_{i=1}^k\binom{n - i}{k - i} f_i\),计算出 \(g_k\) 后容易 \(O(n^2)\) 还原出 \(f_k\)。
那么 \(g_k\) 是容易的,大致就是一个 \(\binom{n - 1}{k - 1} \times k!\)。
考虑带限制怎么整。考虑直接枚举 LCP,有 \(O(n^2)\) 种情况,钦定一个后缀然后再计算后面的东西。前面钦定的若干个数将原来的整个区间划分成了若干个区间,不过计算方法仍然是相同的。注意到前面枚举的 LCP 也需要计算划分的方案数,这样整就变成 \(O(n^4)\) 了。
考虑优化,首先最后枚举 LCP 的划分方案数可以优化掉,因为最后大致是要造成一个形如 \(ans_{i + j} \gets ans_{i + j} + v \binom{k}{j}\) 的贡献,那么我们可以转成格路计数,变成一个 \(O(n^2)\) 的 DP,这样最后一步就优化掉了。而注意到每个 LCP 进行的贡献可以写成一个四元组,而在枚举 LCP 最后一位是什么的时候产生的不同的四元组是 \(O(1)\) 级别的,于是我们可以先计算这样的二元组都有多少,然后在合在一起计算,这样就优化到 \(O(n^2)\) 了。
感觉这个十分体现了 步步为营 的优越性了。写了两份 \(O(n^4)\),一个 \(O(n^3)\),一个 \(O(n^2)\)。
2023.9.21
呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃。
感觉这 b 题单给我做恶心了,一天做两道题是不是挺傻逼的啊,但是这阴间难度题真的有点做不下去。
CF1696H Maximum Product?
首先考虑给定一个集合如何计算最大成绩。显然优先选绝对值最大的。如果前 \(k\) 大的乘积为正那么就是答案,如果为负那么可以将绝对值最小的一个负数换成绝对值最大的正数,或将绝对值最小的正数换为绝对值最大的负数。注意如果集合中只有负数且乘积为负,那么应当选绝对值最小的。
然后考虑 DP。首先按照绝对值从大到小排序,这样我们可以先 DP 枚举选择了 \(k\) 个数后,最小的负数为 \(i\),最小的正数为 \(j\) 的总权值。直接暴力 DP 是 \(O(n^4)\) 的,前缀和优化可以优化至 \(O(n^3)\)。
如果乘积为正数,那么后面的随便选即可。如果乘积为负数,考虑枚举后面选的绝对值最大的正数和负数 \(p, q\)。那么容易计算出最大值是多少,然后对于其它数的选择,\(p, q\) 之间的正数或负数可以任意选,\(q\) 后的所有数都可以任意选。然后就是若干个 \(2\) 的幂。暴力做就是 \(O(n^4)\) 的。然后发现如果枚举了 \(p\),首先 \(\max\) 可以拆开,\(q\) 的区间是单调的,容易发现分界点也是单调的,所以可以直接维护指针。然后幂也可以拆开,前缀和优化一下,就可以将所有 \(q\) 的答案 \(O(1)\) 得出了。然后注意一大堆情况,比如后面只选负数,只选正数,啥都不选,还有前面是否选了正数(一定选了负数,所以不用考虑这个),等等。
代码极其难写,最好的办法应该是写一个 \(O(n^4)\) 代码出来之后再一点一点优化。\(O(n^4)\) 的各种分类讨论就很恶心了,写了一上午,呃呃了。然后还被卡常,呃呃呃呃呃。
似乎有更好写的做法,麻了咕了,恶心死我了这题。
P7907 [Ynoi2005] rmscne
哈哈其实是模拟赛考过的,今天 SoyTony 发现是 Ynoi 的,来水一题,当今天多过了一题。
考虑扫描线维护答案。对于一个左端点,维护以它为左端点的最小右端点。考虑每次向右拓展时,对于 \((lst_i, i]\) 中的所有左端点,它们必须要包含当前这个节点,所以将它们所有的右端点全部设为 \(i\)。考虑如何查询,首先左端点必须在一段区间内,因为如果太短则不能覆盖所有值。考虑再记录一下每个点的区间内有多少数,那么取出现的数最多的区间就一定覆盖了所有的数,这样就很容易在线段树上维护了。
CF1098F Ж-function
先口胡一下,真的不想写代码了,先咕一咕。
首先答案等于 \(\sum_{i=l}^r \min(r-i+1, \mathrm{lcp}(i, l))\)。
把字符串翻转一下,然后建个 SAM,然后现在相当于要求 \(\sum_{i=l}^r \min(i - l + 1, \mathrm{len}(\mathrm{lca}(p_i, p_r)))\)。
这样我们把问题转化成了树上问题。
发现这个东西与 P4211 [LNOI2014] LCA 很像,只是少了一个限制。
然后有两种做法:(有若干种做法,写了两个我看懂了的)
可以先按照上面那题的树剖线段树的思路来做。考虑将贡献拆到 \(\mathrm{lca}\) 到根的路径上。考虑如何限制 \(\min\),可以将对边的贡献改成一个多重集,在查询时只考虑其中 \(\ge l\) 的所有数有多少个,具体的考虑将 \(u\) 向父亲的边的边权设为 \(i - \mathrm{len}(u) + 1\),这样所有 \(i - \mathrm{len}(u) + 1 \ge l\) 的值就有 \(\mathrm{len}(u) \le i - l + 1\) 个。
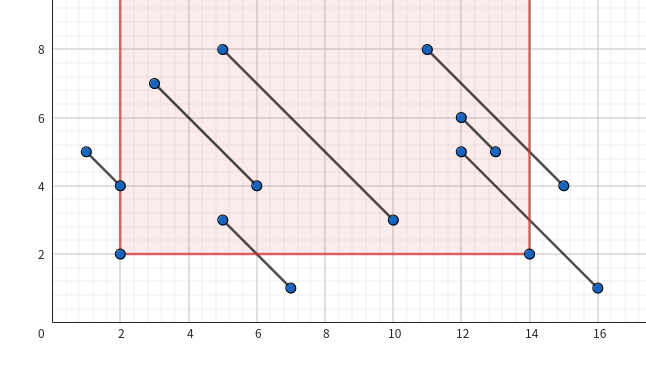
考虑树剖之后,我们的操作相当于在二维平面上插入 \(\log\) 条斜率为 \(-1\) 的线段,每次查询相当于查询一个矩形与这些线段的交的长度和。
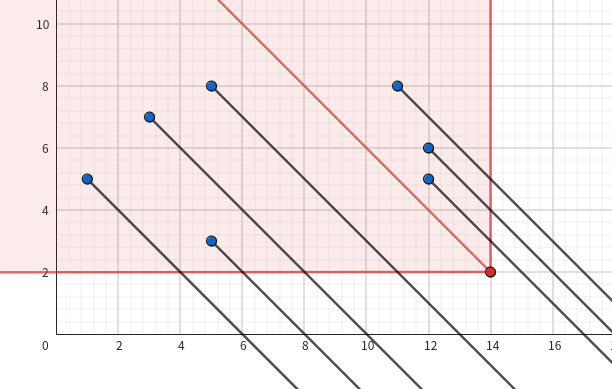
考虑将线段差分成射线,然后查询射线与矩形的长度即可。查询区域同样可以差分成一个点左上角的所有区域。我们按照交下边界与交右边界分类,然后发现我们其实就是在查询两个三角形区域内的所有点的横坐标 / 纵坐标 / 点数之和了,这个容易写成二维偏序的形式,加上查询点的限制就是一个三维偏序,复杂度 \(O(n \log^3 n)\)。我不知道能不能过。好像精细点讨论就能 \(O(n \log^2 n)\) 了,但是题解看着太长了不想看。
感觉应当是优秀多了的做法,但是还是不想写。
考虑两个点的 \(\mathrm{lca}\) 实际上是两个点的路径上深度最小的点,所以 \(\mathrm{lca}\) 相关的问题也可以用点分治解决。我们设当前分治中心为 \(x\),那么考虑 \(p_r\) 与 \(p_i\) 的位置关系:
- 若 \(p_r, p_i\) 均在 \(x\) 的子树内:那么它们的 \(\mathrm{lca}\) 就固定是 \(x\),只需要讨论 \(\min\) 取哪边即可,范围很容易得出,只需要求子树内一个区间内的点数与编号和即可;
- 若 \(p_r\) 在子树外,\(p_i\) 在子树内:那么它们的 \(\mathrm{lca}\) 在子树外,且对每个 \(p_r\) 是固定的,可以在建点分树的时候预处理出来,然后做法就和上一个情况一样了;
- 若 \(p_r\) 在子树内,\(p_i\) 在子树外:那么它们的 \(\mathrm{lca}\) 只取决于 \(p_i\) 是什么,那么还是考虑 \(\min\) 取哪边,如果 \(i - l + 1 < \mathrm{len}(\mathrm{lca}(p_i, p_r))\),则 \(i - \mathrm{len}(\mathrm{lca}(p_i, p_r)) < l - 1\),加上 \(l \le i \le r\),这是一个二维偏序的形式,直接维护即可。
这样总复杂度就是 \(O(n \log^2 n)\)。
2023.9.22
一天两道 *3500 做破防了,换点轻松的题做做。呃呃。
下面 QOJ 的题基本都来源于 The 1st Universal Cup. Stage 2: Hong Kong。
QOJ5457 Painting Grid
首先如果 \(n > 2^m\) 或 \(m > 2^n\) 那么一定无解,若 \(n, m\) 均为奇数显然也一定无解,那么以下默认 \(n\) 为偶数。
那么我们考虑将整个矩形划分成上下两半,下半部分由上半部分翻转得来,那么出现次数的限制显然能够满足。那么我们现在得到了一个 \(\frac{n}{2} \times m\) 的网格,这里分两种情况:
-
\(m \ge 2^{\frac{n}{2}}\):那么发现,此时我们可以简单的每一列分别填入 \(0,1,2,3,\cdots2^\frac{n}{2} - 1\) 的二进制表示,循环填入。此时我们一定有不超过 \(2^\frac{n}{2}\) 次 \([0, 2^{\frac{n}{2}})\) 的循环(因为有 \(m \le 2^n\)),且可以保证每一行均不相同。
而由于上下两部分是翻转得来的,所以相当于下半部分也有不超过 \(2^\frac{n}{2}\) 次 \([0, 2^{\frac{n}{2}})\) 的循环。而这 \(2^{\frac{n}{2}}\) 个数可以构成 \(2^n \ge m\) 个二元组,于是我们可以按照这样的二元组填入每一列,就能保证每一列互不相同了。
具体构造就是将前几个整循环每次循环移位一个,剩下的散块不动即可。
例如:
\[\begin{aligned} \texttt{01230123012}\\ \texttt{12302301012} \end{aligned} \] -
\(m < 2^{\frac{n}{2}}\):此时按照上面的构造方式可能出现两行均为 \(0\) 的情况,但是此时我们一定可以构造出一个矩形满足每行每列不相等。具体方法是先填入一个对角线,然后剩下的依次填入没有填入过的二进制数。可以证明,这样的构造一定能满足矩形与直接翻转后的矩形的每一行均不相等,证明大概就是对于 \(m\ge 3\) 对角线所在的行翻转后不相等(\(m=2\) 需要特判一下,因为对此时翻转后可能相等,实际上只有 \(n=4,m=2\) 需要特判),若 \(m \le \frac{n}{2}\) 则除对角线以外最高位一定都等于 \(0\),翻转后都等于 \(1\),所以也是互不相等的。
QOJ5458 Shortest Path Query
DAG 上最短路是很经典的问题,拓扑排序 DP 即可。
但是本题的边权并不一定,不过我们仍然能够记录所有到 \(u\) 点的路径,将一条路径记为 \((x, y)\),表示经过了 \(x\) 条白边,\(y\) 条黑边,那么这条路径的真正长度就是 \(ax+by\)。
容易发现,\(ax+by\) 的最小值一定取在一个凸包上的点,于是我们只需要维护 \((x, y)\) 的凸包即可。
可是凸包大小似乎还是 \(O(n)\) 的,看起来仍然无法通过。注意到这个凸包是一个整点凸包,且横纵坐标之和不超过 \(n\),于是可以分析出凸包上点数的最大值为 \(O(n^\frac{2}{3})\)。
证明:考虑凸包是由若干条向量组成的,这些向量必定互不相等,设所有向量的 \((x_i, y_i)\) 满足 \(x_i, y_i \le m\),那么这样的向量最多有 \(O(m^2)\) 个,且向量横纵坐标总和为 \(O(m^3)\) 级别的,于是点数的数量级就是 \(O(n^\frac{2}{3})\) 的。
那么每次直接归并合并凸包,查询时凸包上二分,复杂度就是 \(O(m n^\frac{2}{3} + q \log n)\)。
QOJ5464 Dice Game
其中 \(d_{i,j}\) 表示 \(i\) 的第 \(j\) 位,\(c_j\) 表示 \([0, n)\) 中第 \(j\) 位为 \(1\) 的数的个数。
设 \(v_i = c_i 2^i\),那么后面就是给 \(v_i\) 加若干正负号的和。发现 \(v_i\) 与 \(v_{i - 1}\) 的差距应当是很大的,所以低位对正负性影响应当是较小的。打表可以发现,符号相同的段大致是有 \(O(\log n)\) 段,于是我们如果能找出这些段就可以将 \(\max\) 拆掉了。
考虑二分找每一段的端点,那么我们需要判断一段内符号是否相等,这可以通过数位 DP 找出区间内的最小值 / 最大值实现。同样求和也可以通过数位 DP 求出答案,总复杂度 \(O(T \log^3 n)\)。
2023.9.23
早上搜索 Rick Astley,然后电脑死机了。好好好。



你们波兰人出比赛这么放飞自我吗??
P9062 [Ynoi2002] Adaptive Hsearch&Lsearch
考虑朴素平面最近点对的做法。平面最近点对的做法基本都基于“若当前点集中最近点对为 \(d\),那么每个 \(d \times d\) 的区域内的点数一定是 \(O(1)\) 的”。比如分治法计算跨中心点对时,只需要枚举 \(d \times d\) 的区域内的点对,非分治法每次加入一个点,同样只枚举 \(d \times d\) 的区域内的点对,随机增量法也是一样的做法,随机打乱后,每次按照 \(d \times d\) 划分成若干个网格,每次加入一个点只查询周围的几个格子,若 \(d\) 减小则重构。
注意到一个重点:上述算法中,将 \(d \times d\) 改成一个 \(kd \times kd\)(\(k\) 为一个小常数),点数仍然是 \(O(1)\) 的。那么考虑用有限个网格来满足所有查询的需求,我们令 \(d\) 分别等于 \(2^0, 2^1, 2^2, \cdots, 2^{\lceil\log_2 V \rceil}\),进行 \(O(\log V)\) 次划分网格,这样就不需要随机化重构了。这个做法看起来更有前途,所以考虑拓展。
本题要求区间查询,而容易发现很多点对是没有用的,若 \(i_1 \le i_2 < j_2 \le j_1\) 且 \(\mathrm{dis}(i_1, j_1) > \mathrm{dis}(i_2, j_2)\),那么 \((i_1, j_1)\) 一定是不可能作为答案的。那么我们可以考虑找出有用的支配对,可以猜测这样的支配对数是 \(O(n \log n)\) 的。
具体而言,我们假设最后的答案 \(d \in [2^{k - 1}, 2^k)\),那么发现,如果我们将点按照 \(2^k \times 2^k\) 划分网格,那么最后的点对要不然在相邻的两个格子内,要不然在同一个格子内。但是考虑这样的点对仍然会很多,但是我们注意到,同一个格子内两两距离均大于 \(2^{k - 1}\) 的点的个数是 \(O(1)\) 的,那么我们可以只考虑同一个格子内编号相差 \(O(1)\) 的点对,如果编号相差再多那么必定存在距离 \(< d\) 的点对,此时就一定不会造成贡献了。相邻格子同理。因此,一共能找到 \(O(n)\) 个支配对。对于每一个 \([2^{k - 1}, 2^k)\) 都找出这些支配对,就得到了 \(O(n \log n)\) 个支配对。
那么现在问题就变成了简单的区间内点对 \(\max\),注意到点对很多而查询较少,所以可以使用 \(O(1) - O(\sqrt{n})\) 的分块来平衡一下复杂度,这样总复杂度就是 \(O(n \log V + q \sqrt{n})\)。
QOJ5511 Minor Evil
首先容易发现,如果 \(b_i\) 不在 \(S\) 中,那么这个操作一定不会进行。那么也就是说,最后所有 \(S\) 的球都是黑色,其它的都是白色。
正着考虑不好考虑,可以反过来做。先将 \(S\) 中的所有球看做黑色,将操作看做是:若 \(a_i\) 是白色的,\(b_i\) 是黑色的,则将 \(b_i\) 变成白色,问能不能使得最后所有球全部是白色。发现这样每次操作肯定能操作就操作会更优,于是直接贪心做即可。
QOJ5507 Investors
很简单,但是我脑瘫了。
首先发现,进行的操作一定会对一个后缀进行。因为如果某次操作不是后缀,那么将右端点扩展为最右一定不会更劣,原因显然。
而容易发现,如果每次操作都是后缀,那么显然令加的数极大最优,这样将序列划分成了若干块,每块之间不存在逆序对。这样就变成了将区间划分成 \(k+1\) 段,使得每段逆序对和最小。众所周知区间逆序对数满足四边形不等式,直接决策单调性优化即可。
2023.9.24
这几天做的题是不是都有点无意义。
当摆会了,哈哈。
新叶喵:
.:+??-_~l^
. ."I,'
. . '<}]_+><_]]+:. '`^,;I!I^'.
. `-1]--____-]{1?;. '";i_][}[?~_}>`^'.
. '-(}[]]]]r\}[}1(|]:. .. ...'.'''...':>?{(\\|(){[[-?{_`^^`.. .
..!\)1{{{}xQQj1((((\|_^..'`^""",,,,",,I<?1\\\\|||(((tuf){(i'``^`. .
...... .'[\)))))tLU)<+)\(|||\)i,:;lll!!!!l>_}(\\\||||||\)}?uCt)():'``^'.. .
.'.. . ^)\(((((xr]<<<~)\(|||\\\1]-______-}(\\||||((\/)]~<<(J/(/_`'`^`. ..
... .. .. .^1\|||||f{<~~~<+uv|(|||j]<~<<<<<<<<<?1|\|/rcr[~<<~<)v(\)l^^'. . .
. ...'``^`. ...'_t|||||\]<~~~~<]mwx|||\-<<~~~~~~~~~<~_]{cdn+<<~~~<)/|/<",::^. .. .
. ..""""",,.. .. ")/||||\1<~~~~~in#hv(|?<<<~~~~~~~~~~<~+<_t]<<<<>>]/xv_,""",::"' . ..
..'^""",^ lt/((((|}<><<<+z0Lr}--??_+~<<<<~~<~?1|{~>+-++?(umqX+",,,,,"",:,` .
. ..'''''''''''.+QYfruvvr}+_[(t)-~<_\\\\|({[?~<<_1||(\{<<<~nqkoL[;,:,,,,,,,"",:"' ..
. '^",""","",",{J0qpkkkpX\\1_<<<>_\||||||||)]_))1)(|f[]]?{m0\-~:::;:,,",,,,"",:"...
. . .","""""""""":>>!cmZmpkhJ]_<<+-?])ft//\(()111)111|jJmZYjj?{[<i]I::::,,,,,,",,""::` .. .
. ...,,"""""""""";_!,,_X000qX_<~{)|/fQpqZJcnr){{{}}}{{tJ*qzoY/(+{>1?::::;:,,,",,",,""";". .
. . ':^"""""""""^>];I!!~)xv{><~~)\tfkW&&bUkYnf{}}[[}}}|Q@%omv<|~/v|!I;:::;:,,","",,,,"":,.
. `>" ... ..:""""^"""""^;}(()}_><+~<~~<+)\\bh@$@8bO-(1}[[]]]][upbJz{i1>tr]?_-l::::","",,,,",""";:..
. '>?+". .. ',",:;;,""^":!-1tff)-+~~~~~<+)?vXOdbQzr;(\1{}}}{{{f/(/1<-~<(f)]<l::::;,,,,,"",",,""";,.
I_Il>i;'..^:<++_--__~i;!_+<~-]}tx]<<~~~<+??/f/\\|<!?][}}{(trf1?++<~<<+)~[<:::::::,",,,,,,,","""";^
.....~>I;;!+_+?[}?~~<~<~~+___>!!~?{1}{_~~~<<<<~+++-__+_?][}{1)(jvf{{}[]]][xZt])l::::::",,,,,,,,,,,""",;. .
.'^^^^^_+!!!!!>~~~<<~~~~~~~~<<~_-~l?~-}1)jzXYr)-__--]}{)(||\||||cUv\(((|(|j?!{n|-;::::;,,,,,,",,",,,"""";`.. .
."^^```!{_>>>><<<~~~~~~~~<<<~~~~<_]-?)?-[11)\fLufjxnnrf\\|(((|((rj|fnvnt|tx~":~i:::::::,,",,,",,",,""""";^ .
.""^^^^^<({?_~<<<<<~<<<<<~~~<<<<<+][-?+_1rXLZmkJf\/xcvJZpdbdpmOmmwbQCUnf/\\<::,:::::::,,,,","",,",,""""";^ .
..`^"^^^'I{\())1{[?_-[\xvzXzcnf|[-~<<<~~<<<+[rQhkmCcxrncY0pkbh#kbm0fjxrttr{;:::::::::,,",",,,",,",,""""";`..
..... `<)\\tjxxxncYJCQQ0ZmbL?<<~~~~~~<<~<>~{xLdhwYccccccULQr_]czzzXJLx!::::::::,,",,,,,,,",,,"""""",;. ..
. .^>{|/fxucXXYYUJJJJX-<~~~~~~<+)]<~~~<><]xmZccccczccccrczvXQXx(i::::;::,,,,,",,,,,,,,,""""",";`
... .,i-}|ncYYYcxt\r-<~~~~~~~>|L{<~~~~}rYQ0OO0QC0dwzcczcLw0Un|[<;::::,",",,,",",,,,""""""""";^
i(|xt[+i>[([<~<~~~~<<(zt+<><<<<+])/xczznrxJZXccYOc?~!;::,,,"",,,",,,,,,",""""""""",;^...
....<t{:;_--]?+<~~<<<<<}xUUUzf){}{\\<>>>~_{jfftuCzCZCul",,,,,,"",,,,",,,,,,""""""""",:,'...
";<}_<<~<~~~~++?(uJCJYn1_{\jncYf_<<~<<|xrnuXJJYUY<",,,,,",,,,,,,,,,"""""""""""::^. ..
..'"i-]-~+__--?]]?{rucnt)_!"`^^",;i_{/{?+~<+}}xJYYUUXn[:"",,,,,,""","""""""""""",:,^. ...
.. :{[-_--_}?__+<I,"::,"^^^^"^"""""^^^;<-]-_~<<-fJJv\?~?+,""""""""""""""""""",::,^'..
..':lll,`.`"`'.'`"""^^^^^^""^""""""""^^",;>?]+<<{u{~<<<]<""""""""""",,,,:,","`.. ..
..'`^""""^""^^""^""^"^^^`''"i]_>!_}-+~<~?<;,,,,,:,,,"""^`'..
.. ..'``^^^^^^^^``'... `l<<<l,i+_<i<?l''''..... ..
.`' .`;i>>!^
..... .

QOJ5500 Bars
考虑一个简单 DP:设 \(f_i\) 为选中 \(i\) 为关键点的贡献,那么考虑中间的数的贡献,就有:
看起来像是斜率优化的形式,但是拆开之后发现斜率优化并做不了。
首先发现第一个点与最后一个点选上一定不劣,那么贡献相当于就是 \(\sum_{i=2}^m(w_i - w_{i - 1})(p_{w_i} + p_{w_{i - 1}})\)。后者发现是与梯形面积公式是很像的,我们如果先全部除以一个 \(2\),发现贡献就变成了若干个点形成的封闭图形的面积。那么这就是个很显然的问题了,选若干个点使得封闭图形面积最大,肯定是选一个凸包最优,那么直接求凸包即可。
QOJ5510 Line Replacements
首先考虑什么状态下是合法的。
首先发现,如果一条路径跨过了一个关键点,那么我们可以将这个路径拆成两条路径,那么相当于我们可以在关键点的地方将树分开,看做几个子问题。每个子问题相当于路径两个端点必须是叶子(若存在一个叶子不是关键点显然是无解)。直接考虑路径不好考虑,我们直接考虑穿过某个点的所有路径。由于我们知道每条边有多少路径,那么对于某个点来说,问题可以看做将若干路径两两配对,是否能够全部匹配。这是一个经典问题,若存在一个子树路径数大于总数一半那么一定不可能全部匹配,否则如果为偶数则能够全部匹配。容易发现,如果对于每一个点都满足这样的条件,那么一定是合法的。
考虑原问题。每次删边不好考虑,反过来变成加边。那么我们先把所有边删掉,看剩下的每个连通块是否满足条件,如果不满足那就直接无解。然后考虑按照什么顺序加边。我们加边肯定是要尽可能满足条件。发现限制条件有两个:最大值不超过总数的一半,不能是奇数。如果某条要加的边的边权是奇数,那么直接就一定无解了,否则后面的条件一定可以满足。最大值不超过总数一半,那么肯定是让最大值尽可能小,那么我们按照边权从小到大的顺序加边即可。如果出现不合法装填就是无解。
QOJ5503 Euclidean Algorithm
可以发现,\(2a-b\) 就是 \(a\) 关于 \(b\) 的对称点,那么也就容易发现,这种算法能够得到的最小的数为 \(x \bmod (y-x)\)(或等于 \(x\))。
那么也就是令 \(d = \gcd(x, y), k \ge 1, p \ge 0\),则所有合法数对必须形如 \((pk+d, (p+1)k+d)\) 且满足 \(\gcd(pk+d, (p+1)k+d) = d\)。
容易发现这等价于 \(\gcd(k, d) = d\),即 \(d | k\),那么合法数对就一定形如 \((pkd+d, (p+1)kd+d)\),满足 \(k \ge 1, p \ge 0, d \ge 1\)。
计数就很容易了,这实际上就是要求 \((pk+1)d \le n\) 的正整数 \((p, k, d)\) 对数(这里令 \(p \gets p + 1\) 了),直接枚举 \(d, p\) 计算合法 \(k\),答案就是:
直接整除分块套整除分块就能做到 \(O(n^\frac{3}{4})\),由于时限 30 秒,可以通过。好像枚举 \(p, k, d\) 中最小值然后再做就是 \(O(n^\frac{2}{3})\) 了,咕了。
最小值一定是 \(O(n^\frac{1}{3})\) 级别的,于是就有:
2023.9.25
事实证明我已经不知道这个做题纪要要多长时间开一个新博了。感觉快变成每放假一次开一次新博了。
做没有题解的题还挺痛苦的。呃呃。
做一个题想了一下午,题解写完了然后发现我把这题当 MO 题做了,能构造方案但是没法维护,傻逼了。
然后写这题题解死机了一次,写代码写一半又死机了一次。我他妈。
QOJ5506 Hyperloop
做法其实很简单,这就是个很直接的最短路问题,路径字典序最大容易拿主席树维护哈希实现,与 CF464E The Classic Problem 做法类似,不过这个题不用处理进位问题,直接维护哈希即可。
稍微恶心点的是空间限制,如果直接在每次尝试松弛的时候都进行一次线段树操作,空间复杂度是 \(O(m \log \max\{c_i\})\) 的,由于线段树空间大致是 \(16\) 个字节的常数(记录左右儿子与哈希值),空间正好是开不下的。但是实际上,我们并不需要每次松弛的时候都进行线段树操作,在二分哈希的过程中我们是可以直接计算出加入一个数后的哈希值的,所以我们只需要在每个点的最优决策确定后再修改当前节点的线段树,这样空间复杂度就是 \(O(n \log \max\{c_i\})\) 的了,可以通过。
QOJ5504 Flower Garden
发现题目给的限制很像一个 2-sat 问题。
考虑转化一下第一条限制,\([a_i, b_i]\) 内的所有数全是 \(\texttt{0}\) 或者 \([c_i, d_i]\) 内的所有数全是 \(\texttt{1}\),意味着如果 \([a_i, b_i]\) 中任意一个数为 \(1\),那么 \([c_i, d_i]\) 中的所有数就都必须为 \(1\),那么我们建一张图,让 \([a_i, b_i]\) 中的所有点全部连向 \([c_i, d_i]\) 中的每一个点,那么一种 \(\texttt{01}\) 序列合法当且仅当 \(\texttt{1}\) 对应的点在这张图上为一个闭合子图。
第二个限制相当于这个闭合子图的大小 \(\in [n, 2n]\)。发现选中一个点后这个点所在的强连通分量一定都选,那么缩点得到一张 DAG,在 DAG 上选一个闭合子图使得权值和在 \([n, 2n]\) 内。那么我们分两种情况:
- 选择的点中权值全部在 \([1, n)\) 内:那么容易发现可以随意选直到权值和落到 \([n, 2n]\) 内,如果可以选那么一定可以选到这个区间内;
- 选择的点中权值有 \([n, 2n]\) 内的:那么权值和一定 \(\ge n\),那么我们需要选尽可能少的点使得其能够进入 \([n, 2n]\) 的范围内,于是只选这个点的后继节点即可。这样的点不超过 \(3\) 个,所以直接暴力即可。
2023.9.26
哈哈,Stage 3 做完了,然后要干啥啊。
QOJ5508 Job for a Hobbit
首先判断无解,考虑每个颜色的个数 \(c_i\),那么如果 \(\sum \lceil\frac{c_i}{k}\rceil > n + 2\) 那么显然无解,否则一定可以构造解。
最终状态一定会有若干柱子上不是满的,但是如果不是满的会导致固定完一行之后后面的空位减少,可能构造会很困难。所以我们先考虑构造出一种满的方案,然后再将这个满的方案变成最终状态。容易发现,如果我们按照从左往右,从下往上的顺序依次将颜色相同的环填入,这样我们就可以从右往左,从上往下将每个环放到最靠右的位置,就能构造出最后的方案了。
那么我们现在的问题变成了,要将 \(n\) 个柱子上的环重排列成给定的方案。发现每次构造完一个柱子后,空柱子仍然是 \(2\) 个,于是我们就可以这样递归去构造,那么我们只考虑如何构造一个柱子。考虑将所有柱子全部移动到最右边,将左边第一个柱子作为要构造的位置,第二个柱子为空。那么每次我们找到一个需要移动的环,我们将这个环移动到第一个柱子上,这样就能构造出来了。
具体来说,我们可以先将第二个空柱子移动到需要移动的环的前一个柱子,然后将这个环的上面所有环(包括这个环)全部移动到空柱子上,然后将左边的柱子上的所有环全部移动到右边(显然一定能移动空),这样就将所需移动的柱子和空柱子向左移动了一位,一直重复即可。有一种特殊情况,就是当柱子是满的且所需环在最底下时,移动完之后左边的柱子没法移动到右边,但是由于没有移动完,左边必定存在一个柱子不满,那么可以将顶元素整体向左移一位,将这个柱子变成非满,然后按照上面的做法做就可以了,最后把顶元素再右移回去。
P9482 [NOI2023] 字符串
两个月了,还是决定来直面梦魇了。
再去看这道题,好像 72 分真的是极其平凡的,甚至 100 分也是十分容易的,真的不懂当时考场上为啥就没想到特殊性质 B 怎么做。看字典序大小没有去想后缀数组...考前确实也复习 SA 了,鉴定为写 SAM 不写 SA 导致的,大致状态也是真的不好吧,可能过完 T1 就想直接求稳开始打纯暴力了,但是不知道为啥我内心完全认为 T2 可做却仍然没想到怎么做。而且好像说暴力枚举回文串能拿大量分来着?并不知道了,待会写写看看吧。
那其实理想分数分布就是 5+100+100+70+36+100+72+30=513 或者 5+100+50+36+100+100+30=521 了。理论可行分好像能达到 5+100+100+70+52+100+100+30=557 了?确实可行性极大,只能说还是我弱智。算是解了个心结?或者算是觉得自己更加弱智了?我不好说。
感觉还是时间掌握不行了。D1T2 如果写暴力写的早些的话试着去发现性质也很容易发现答案是可以找规律的,试这个应该是很容易想到的。这个 72 分和正解也不知道为啥想不到了,真的不好说了。
算了还是看题。
- 暴力:\(O(n^2)\),枚举中心然后向左右拓展就能直接预处理出所有答案,考场上打了的就不说了;
- 特殊性质 A:随机字符串说明两个串的 LCP 不会很长(打表大致得到有 \(100\) 左右来着),于是小于等于 \(100\) 可以暴力判断,大于 \(100\) 的可以规约到特殊性质 B。跑个 SA 就能 \(O(1)\) 判断。
- 特殊性质 B:注意到比较两个子串大致是可以用两个后缀大小关系来刻画的(正串加反串一起跑 SA),仅有两个子串相等的时候会判断错误,而特殊性质 B 满足相邻字符不相等,说明不存在子串相等的情况,那么 SA 是可以直接判断正确的。那么直接跑 SA,问题变成了求 \(j \in [i, r], rk_i < rk'_j, (j - i)\text{ is odd}\) 的 \(j\) 的个数,这就是一个显然的二维数点问题,容易 \(O((n + q) \log n)\) 解决。
额,72 分拿到了。真的不知道考场上咋想的。这个特殊性质 B 应该是很直接会有思路的,但是并不知道我为啥啥都没想到。感觉状态确实还是太差。
考虑特殊性质 B 做法的问题在于,如果两个子串相等,有可能会多算一些答案。注意到,如果两个子串相等,那么这个串一定是一个回文串,那么我们就是要考虑将回文串导致的多算的贡献去掉。据说由于数据里的字符串回文串数量不多,直接暴力枚举所有回文串去重就能过了。
跑一个 manacher,求出以每个中心 \(i\) 的最长回文半径 \(c_i\),那么一个 \(l\) 对应的是回文串等价于 \(l \ge c_{i + l}\),令回文中心 \(j = i + l\),就有 \(j - i \ge c_j\),即 \(j - c_j \ge i\),同样再加上 \(j \in [i + 1, i + \frac{r - i + 1}{2}]\) 的限制,就能统计出区间内有多少回文串了。(或者直接大力 PAM 也容易统计)但是并不是所有回文串都会额外统计,我们只考虑那些 \(rk_i < rk'_j\) 的回文串,而容易发现这两个串的 LCP 后一位一定等于以当前点为中心的最长回文的左右两个字符,这两个字符是固定的,所以可以直接确定哪些 \(j\) 是会被多算的,只统计这些 \(j\) 的贡献即可。这又是一个二位数点问题,直接做即可。总复杂度 \(O(n + q) \log n\)。
额,一点障碍没有的把这题想完了,也可能是因为我已经知道了这题要用什么算法所以很容易想吧。但是确实不懂为啥当时我就想不到了。感觉这题想到 SA 就做完了。感觉跟 D1T2 想到能打表找规律就 70 分了一样。呃呃了。算了,就这样吧。
CF1495E Qingshan and Daniel
不太懂是个什么神秘题。
总之首先肯定能确定哪个队伍会先出光牌,那么这个队伍的出牌数显然是确定的了,那么考虑另一个队伍的出牌。
首先发现可以将出牌序列看做若干个连续段,那么出牌顺序一定是交错的。如果第一个队伍不是输的队伍,可以先模拟出一张,然后就是一对一的关系了。
然后这个问题就类似于一个环上的匹配的东西了,可以感性理解发现此时顺序并不重要,因为无论怎么发牌,每次取得一定是最近的,不会有更远的被匹配到,于是可以把所有牌拿起来一起匹配,直接拿个计数器维护一下即可。
2023.9.27
whk,摆了,十月再见。
兔子:




