2023.9 做题纪要 #1

1.2023.9 做题纪要 #12023-08-31

2.2023.9 做题纪要 #22023-09-15 3.2023.10 做题纪要 #12023-10-03 4.2023.10 做题纪要 #22023-10-16 5.2023.10 做题纪要 #32023-10-25 6.2023.11 做题纪要 #12023-11-06 7.2023.12 做题纪要 #12023-12-11 8.2023.12 做题纪要 #22023-12-19 9.2024.1 训练纪要2024-01-01 10.2024.2 训练纪要2024-02-15 11.2024.3 做题纪要2024-03-19 12.2024.4 做题纪要2024-04-07 13.NOI 2024 前做题纪要2024-05-25

2023.8.31
2023.9.1
2023.9.2
2023.9.3
2023.9.4
2023.9.5
2023.9.6
2023.9.7
2023.9.8
2023.9.9
2023.9.10
2023.9.11

2023.8.31

虽然不是九月吧，但是马上就九月了所以直接并到九月了。

开始板刷 AtCoder 紫题，~~提高紫题通过量~~提高过简单题的速度，就当熟悉下新机房了。

ABC134F Permutation Oddness

排列很难考虑，把它看作一张图，那么怪异度就是所有线段长度之和，考虑对这个图进行 DP，从左到右确定连边，记录有多少边往右连有多少边往左连，当前点一定有一个入边一个出边，然后讨论一下当前点怎么连就行了。发现当前向右连的边数一定等于向左连的边数，所以可以只记录一个。

ABC135F Strings of Eternity

如果 $s$ 长度小于 $m$ 肯定先补成大于等于 $m$ 。然后其实只需要知道哪些位置能匹配上，这个跑遍 KMP 就可以了。然后我们直接将 $i$ 连向 $(i + m) mod n$ ，得到一张图，如果有环显然就是无穷，否则看最长的链是多长就行了。

2023.9.1

本来打算打下模拟赛的，T4 做过，遂咕之。前三道题口胡完了，懒得写了。

CSP模拟32

T1: 考虑把传播的过程直接拆开，每次走一层，这样一共转移 $d$ 次，时间复杂度 $O (d (n + m))$ 。

T2: 考虑一种构造：

          ·····
     
     ·····

·····


          ·····
     
     ·····

·····

类似的东西。

T3: 图是内向基环树，直接每次贪心地从叶子覆盖然后删点，最后环上枚举断开位置，复杂度 $O (k \times \frac{n}{k}) = O (n)$ 。

T4：可以证明答案在下标模 $12$ 的等价类内是凸的，大致就是发现任意一个和为 $24$ ，所有数不超过 $4$ 的集合都能划分成两个和为 $12$ 的集合，于是 $i, i + 12, i + 24$ 一定满足差分递增，所以大力闵可夫斯基和即可。

继续水题。

ABC137F Polynomial Construction

直接拉插就能 $O (n^{2})$ 了其实。

弱智做法：考虑零点处容易构造，其它的点值全部 $p - 1$ 次方就都是 $1$ 了，所以多项式等于 ${(\prod_{a_{i} = 1} (x - i))}^{p - 1}$ ，快速幂即可。

另外做法：我们能构造出一个函数 $g (x) = 1 - (x - i)^{p - 1}$ ，容易发现这个作用与拉格朗日插值那个作用相同，所以可以用同样的方法去做。这个容易二项式拆开，所以算系数很好算。

ABC138F Coincidence

首先发现如果两个数最高位不相同一定不合法，因为异或得 $1$ 取模得 $0$ ，然后发现如果首位相同那么 $y < 2 x$ ，那么 $y mod x = y - x$ ，即 $y \oplus x = y - x$ ，那么说明就是 $y$ 包含 $x$ ，直接数位 DP 即可。

写一下式子，把没用的常数都去掉，可以得到最后大概等于一个 $w (S) = 2 (D \sum_{i \in S} i + (X - D) | S |) + C$ 。枚举 $| S |$ ，容易得到 $\sum_{i \in S} i$ 的取值范围 $[\sum_{i = 1}^{| S |} i, \sum_{i = n - | S | + 1}^{n} i]$ ，把后面那个常数写成 $p D + q$ 的形式，然后对每一个 $q$ 维护区间并的长度即可。

ABC155F Perils in Parallel

区间异或直接变成差分，这样相当于每次可以将两个数反转，问能否使得最后为 $0$ 。考虑建图，对于每一个连通块，如果其中 $1$ 的个数为偶数那么一定可行，否则一定不可行。随便搜一棵 dfs 树然后贪心做即可。

ABC157F Yakiniku Optimization Problem

首先显然二分答案 $T$ ，然后发现条件变为了有若干个半径为 $\frac{T}{c_{i}}$ 的圆，问是否存在一个点，满足它被 $k$ 个圆包含。不难得出，这个点一定是某两个圆的交点（或某个圆的圆心）。那么我们找出所有的这样的点，然后依次 check 即可。复杂度 $O (n^{3} \log V)$ 。

关于求两个圆的交点：

设两圆心之间的距离为 $d$ ，根据余弦定理容易得出 $\cos α$ ，然后我们可以得到 $D F, E F$ 的长度（注意不要使用反三角函数，精度误差会很大），进而我们可以通过向量加减得到两个交点的位置。

2023.9.2

美好的一天从水题开始。

其实我很困。

ABC163F path pass i

这是不是某场模拟赛的 T1 来着。水提交了。就直接统计不经过一个点的路径数，就是每个连通块任意选两个数，咋做都行。Kaguya 是不是大力推崇 DFS 一遍就完了来着。

不做 ABC 紫了，太有病了。

AGC001E BBQ Hard

no comments.

AGC001D Arrays and Palindrome

酷炫构造，虽然考过。still no comments.

AGC002F Leftmost Ball

$k = 1$ 特判掉。发现白球的颜色是个很难处理的东西，于是我们采取一个优秀的处理方式：~~不处理~~。

考虑我们一开始不管颜色是什么，我们只在一个颜色第二次出现（即第一次出现且没被染色）的时候再考虑这个球是什么颜色。而我们发现一件事情，就是当这个球出现了第二次之后，剩下的出现就可以任意填了，如果我们知道后面还剩下多少空位那就可以直接计算出方案数了。那么我们考虑不记录颜色，最后再乘一个 $n!$ 。这样我们只需要记录当前有多少白球，且有多少个白球对应的颜色还没有出现第二次，那么我们每次要不然是新加入一个白球，要不然就是加入一个白球对应的第二个颜色球，直接转移即可。

AGC002E Candy Piles

很容易把博弈写成在一个阶梯状的形状上博弈的形式。直接写一个博弈 DP。画个图出来，很容易发现规律，直接按规律求值即可。

2023.9.3

上午机房网没了。然后看了一遍化学必修一，看不下去了然后去隔壁交换机把网线拔了重插了一次，网好了。😓

然后 SoyTony 就开始卷 whk 了，我继续颓 AGC。

AGC003D Anticube

考虑到如果我们能把所有数质因数分解了，那么只要把所有指数模 $3$ ，那么只有指数集合加和正好为 $0$ 的两个数不能同时选，这样两个集合选一个最大的即可。

~~那么我们写一个 Pollard-Rho 即可~~考虑到我们很难直接大整数质因数分解，那么可以阈值分治一下。首席按我们可以把指数模 $3$ 的过程手动做一下，直接枚举所有 $p^{3} \leq m$ （以下令 $m = 10^{10}$ ）的质数然后试除即可。这部分复杂度是 $O (n π (m^{\frac{1}{3}}))$ 的。那么我们考虑质因数分解的时候也只分解 $π (m^{\frac{1}{3}})$ 个质因子，那么剩下的质因子就都是 $> m^{\frac{1}{3}}$ 的了，而这样的质因子最多只有两个。假如有两个相同的质因子，我们可以直接判断是不是一个完全平方数。如果不是，那么我们看起来就不好分解了，这怎么办？很简单，~~我们不分解。~~考虑到如果两个质因数都只能出现一次，而其对应的集合就必须出现两次，而两个 $m^{\frac{1}{3}}$ 的质数乘积的平方一定会大于 $m$ ，那么一定不可能会有数和这个数冲突了。那么我们可以直接不处理这个数，直接扔进去了。

AGC003E Sequential operations on Sequence

首先我们可以将所有最小值拿出来，显然只有这些是有用的。然后我们就得到了一个上升序列。我们设 $f (k, l)$ 表示在 $k$ 次操作后前 $l$ 个数的出现次数序列，那么有 $f (k, l) = ⌊ \frac{l}{s_{k - 1}} ⌋ f (k - 1, s_{k - 1}) + f (k - 1, l mod s_{k - 1})$ 。由于一个数每次模完一个数之后至少减半（不变则 $f (k, l) = f (k - 1, l)$ ，于是 $f (k, l)$ 没有意义），所以对于每一个 $f (k, s_{k})$ 来说，后者仅会进行 $O (\log V)$ 次，那么所有有用的 $f (k, l)$ 就仅有 $O (n \log V)$ 个。但是我们直接维护这个序列是不可行的，不过由于我们仅需要查询 $f (m, s_{m})$ ，那么我们可以把这个过程反过来跑一个拓扑排序，记录每个 $f (k, l)$ 被统计了多少次，这样就能得出答案了。

AGC003F Fraction of Fractal

首先我们考虑相邻的两个形状是否能联通。有可能上下联通，左右联通。如果两者同时联通，那么任意一个状态都是只有一个连通块，否则任意情况下都是 $c^{k}$ （ $c$ 是形状里面的方块数）。那么我们只需要考虑一边联通一边不连通的情况，发现这时候每进行一次操作后所有连通块都是每行之间独立的，不可能联通，也就是说形成了若干条链。而链的连通块数有经典的点减边容斥，点显然是 $c^{k}$ ，边有两种来源，一种是新增加的块之间的边，一种是原来就有的边。容易写出矩阵转移，矩阵快速幂即可。

2023.9.4

摆烂。

AGC004E Salvage Robots

贺了。

考虑移动出口而不是移动机器人，每次移动会使得边界缩小。然后就不会了。

发现移动一定会将当前形成的矩形全部覆盖到，那么我们就可以直接记录当前已经访问的矩形 $(l, r, d, u)$ ，通过这个可以计算出当前的边界，然后直接枚举往哪里拓展即可。

AGC004F Namori

弱智了，不会做。

考虑进行一步转换，将图黑白染色，此时操作就变成了将两个不同颜色的点交换顺序。先考虑树的情况，这时候容易得出合法条件是黑点与白点点数相同。考虑每条边被经过的次数，只需要知道子树内有多少点需要更改即可。那么我们给一个黑点设权值 $1$ ，黑点权值 $- 1$ ，那么总操作次数就是所有子树内的权值和的绝对值和，即设子树权值和为 $a_{i}$ ，那么答案等于 $\sum | a_{i} |$ 。

考虑基环树的情况。如果环长为偶数，那么仍然是可以黑白染色的。我们可以先任意找一条边断开，然后做上面的过程。那么考虑这条边的贡献，我们设这条边交换了 $x$ 次，那么就相当于一些点增加了 $x$ ，一些点减少了 $x$ ，相当于贡献变成了 $\sum | a_{i} - x | / | - a_{i} - x |$ ，这是经典最小化问题， $x$ 取中位数即可。

如果环长为奇数，那么发现黑白染色之后会存在一条边两边同色，操作这条边意味着同时修改两点颜色。那么我们可以考虑当前黑白点的差值 $s u m = a_{1}$ ，那么这条边就会进行 $\frac{| s u m |}{2}$ 次操作，那么我们可以直接将这些操作先加上，然后按树做即可。

AGC005E Sugigma: The Showdown

高水平博弈论。只想到了第一步。我菜。

首先考虑什么情况下是永远也抓不到的。容易想到一种情况就是 A 一直在两个节点间反复横跳，这时候需要满足 B 树上两个节点之间的长度大于等于 $3$ 。那么也就是说，当 A 到达一个节点，满足这个节点所在的一条边在另一棵树中长度大于等于 $3$ 时，那么答案就是 $- 1$ 了。我们将所有的这样的点设为关键点。

那么考虑以 $y$ 为根的 B 树上，有若干关键点与若干距离为 $1 / 2$ 的 A 树边。我们可以将博弈问题转化成，A 要通过这些 A 树边到达一个关键点，或尽可能走最多回合，而 B 从根开始追他。

注意到一点，就是 A 是无法穿过 B 的，因为 A 最多只能走两格，而如果 A 通过走两格穿过了 B，B 一定可以回头把他抓住。那么此时 A 一定在 B 的子树内，那么 B 的最优策略也就显然是一直往 A 的子树内走了。那么我们就可以很容易确定 A 能够走到哪些点上了，只需要满足 A 在路径上每个点都不被 B 抓住即可，这个简单模拟即可。那么我们就可以 DFS 一遍知道 A 都能到达哪些点，如果能够到达关键点则答案 $- 1$ ，否则答案为能到达的点的最大深度乘 $2$ 。

AGC005F Many Easy Problems

我做法太弱智了，简单写下。

首先点集连通块大小可以用寻宝游戏的做法去做，按照 dfs 序排序后将两两距离加和除以二就是生成树的边数，加一就是答案。那么大致就是一个 $a n s_{k} = \sum_{S} \frac{dis (s_{1}, s_{k}) + \sum dis (s_{i}, s_{i + 1})}{2} + 1$ 。

拆式子，后面那个 $1$ 显然是 $(\binom{n}{k})$ ，前者考虑枚举每个点对 $dis (i, j)$ 的贡献，发现要不然作为前者要不然作为后者贡献，作为前者就是剩下的数都选在两个数中间，作为后者就是剩下的 $k - 2$ 个数都选在两个数两边，那么就是 $a n s_{k} = \sum_{i = 1}^{n} \sum_{j = i + 1}^{n} dis (i, j) ((\binom{n - (j - i + 1)}{k - 2}) + (\binom{j - i - 1}{k - 2})) + (\binom{n}{k})$ 。

考虑生成函数，中间组合数的生成函数显然是 $(1 + x)^{n - (j - i + 1)}$ （先把 $k - 2$ 看作 $k$ ），这个东西与 $j - i$ 有关系，我们先考虑换元，令 $u = x + 1$ ，那么我们考虑求出 $F (x) = \sum_{i = 1}^{n} \sum_{j = i + 1}^{n} dis (i, j) u^{j - i}$ ，然后通过多项式平移即可得出原答案。

直接把 $dis (i, j)$ 拆成树上差分的形式，然后我们重点考虑怎么求 $dep (lca (i, j))$ 。考虑拆贡献，若一个点能对此造成贡献，那么这两个点的 dfs 序都在这个点子树的区间内。那么我们只需要考虑有多少点对在这个区间内即可，这个是一个二阶后缀和就能解决的事情。剩下的 $dep (i)$ 和 $dep (j)$ 也是前缀加 $1$ 的形式，一阶后缀和即可。

我做法是不是所有题解中最复杂的做法。

2023.9.5

快过去一周了！来看看我都干了些什么吧！啥都没干吧。

早上看了眼 22 高考数学，貌似还好，虽然好像解析几何占大量，我没学过。

为啥我不看 23 高考数学啊。

AGC006C Rabbit Exercise

貌似之前胡策搬过，忘了哪场了。

考虑过一个点对称就是 $2 y - x$ ，那么期望变成 $a_{i} \leftarrow \frac{(2 a_{i + 1} - a_{i}) + (2 a_{i - 1} - a_{i})}{2} = a_{i + 1} + a i - 1 - a_{i}$ ，这个形式非常熟悉，实际上就是将差分数组两个数交换。那么我们的操作就是将差分数组交换若干次，置换快速幂即可。

AGC006E Rotate 3x3

我觉得这个题比前面的那几个紫题都简单吧？？

首先考虑操作本质，发现一列之间的数是不会变的，而且只有正序和倒序两种状态，那么我们先判断是不是这样的，如果不是直接判无解。然后我们把正序看作正数，反序看作负数，那么我们的操作就是将连续三个数取反，并将前后两个数交换。问从初始状态能否变成 $1, 2, 3, 4, \dots, n$ 。

继续观察，发现一次操作会使得奇数位置 / 偶数位置的两个数交换，那么说明奇数位置和偶数位置不可能进行交换，可以再判一下无解。然后我们考虑奇偶的负数个数的奇偶性与逆序对数的奇偶性。进行一次操作后，奇数逆序对数奇偶性改变，偶数负数数量奇偶改变，或反过来。那么我们就必须满足奇数逆序对奇偶性等于偶数负数数量奇偶性与其反过来。

而可以证明，除了以上几种情况外，一定有解。考虑构造使得任意两个位置奇偶性相等的数符号取反的操作。可以先构造两个相邻的数取反，若两个数不在边缘，那么可以通过 $x, y, x, y, x, y$ 六次操作使得 $x, y$ 两个数取反；若两个数有一个数在边缘，设两个数中间的那个数为 $z$ ，那么可以通过 $x, z, x, z$ 使得相邻的四个数取反，再用前面的方法把两个数取反即可将边缘上两个数取反。而剩下的东西容易全部构造出来。那么就容易构造出整个操作序列了。这个自己写一个简单的模拟就很容易发现这样的策略了。

AGC006F Blackout

我不会做。

aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa

首先容易转化成图论模型。首先每个连通块肯定分开计算答案。然后不会了，摆烂了。

考虑对图进行三染色。如果不能够三染色，那么可以构造使得这张图变成一个完全图。证明咕了。

如果能够三染色，但是只有两种颜色，即不存在 $x \to y \to z$ 的边，那么直接输出原边数。

否则每两个颜色不同的点之间都能连边。证明也咕了。

所以直接 dfs 即可。

AGC007C Pushing Balls

高级期望题。单独开篇博写了。

link。

AGC007D Shik and Game

但是这个 D 突然就变得非常平凡了。

首先我们肯定是碰到小熊立刻给糖，这样我们的路线应该是会在中途折返若干次收集金币。注意到，若在某一时刻折返回去拿所有金币，在回来的路上一定也能够将所有的金币收集到。因为相邻两个给糖果的时间差与相邻两个给金币时间差是相等的。那么我们只需要计算什么时候能够拿到折返后的第一个糖果即可。那么可以列出 DP 式子：

f_{i} = min_{j = 1} {f_{j - 1} + (d_{j} - d_{j - 1}) + (d_{i} - d_{j}) + max {T, 2 (d_{i} - d_{j})}}

这个式子很容易数据结构维护，后面的那个 $max$ 可以通过讨论哪个大直接拆开，比较平凡。根据分割点单调还可以使用单调队列优化做到线性复杂度。

2023.9.6

摆大烂。

AGC008F Black Radius

考虑用一个唯一的二元组 $(u, d)$ 表达一个点集。发现，若某一个节点 $u$ 的一个子树完全包含于这个点集，那么这个子树内的所有点都可以表示这个点集，而这说明表示这个子集的所有点一定形成一个连通块，那么我们可以只考虑这其中 $d$ 最小的一个。那么我们只需要考虑什么情况下 $(u, d)$ 表示的子集是 $d$ 最小的。这相当于需要满足 $u$ 的所有子树 $v$ 都满足 $(v, d - 1)$ 与 $(u, d)$ 不相同即可。

同时，我们先不考虑全集，所以钦定所有子集都不能是全集。那么我们考虑什么情况下才会满足这样的条件。

$(u, d)$ 不能是全集：那么只需要满足距离 $u$ 最远的点的距离大于 $d$ ，设这个数为 $m x (u)$ ，那么 $d < m x (u)$ ；
$(u, d)$ 没有出边 $v$ 满足 $(v, d - 1) = (u, d)$ ：首先显然 $(v, d - 1) \subseteq (u, d)$ ，那么我们只需要令每一个 $v$ 都存在一个点 $z$ 使得 $z \notin (v, d - 1), z \in (u, d)$ ，即 $dis (z, v) > d - 1, dis (z, u) \leq d$ 。首先 $z$ 不能在 $v$ 子树内，那么其实后者就不重要了，因为只要存在一个 $dis (z, v) > d - 1$ ，那么一定能找到一个点满足上述条件。那么我们就只需要知道 $dis (z, v)$ 最大的值是否 $> d - 1$ 即可，即不在 $v$ 子树内最大的 $dis (z, u)$ 是否 $> d - 2$ 。而由于我们是对每一个 $y$ 都要求，那么我们只需要满足所有子树中次大的距离 $> d - 2$ ，我们记它为 $s e (u)$ ，那么只需要满足 $d - 2 < s e (u)$ 。

发现，由上面两个条件可以得出 $d$ 的一个上界，那么满足这个上界的所有 $d$ 就都符合条件。

考虑关键点，容易发现加上关键点的限制之后相当于增加了一个下界的限制。因为上述的“若某一个节点 $u$ 的一个子树完全包含于这个点集，那么这个子树内的所有点都可以表示这个点集”，那么也就是说我们只需要找到存在关键点的深度最小的一个子树，那么这个子树就是下界了。这样，我们知道每个点的上下界，容易计算出答案。

AGC010C Cleaning

相对简单的多，感觉到不了紫。

首先容易发现叶子上的数代表往上的路径数。考虑剥叶子，计算某一个节点的子树内一共有多少条叶子往上的路径经过他。根据当前节点的数，可以得知有多少条路径会从这里汇聚，剩下的路径继续往上。我们只需要知道最多有多少条路径可以汇聚在这一点即可。这是一个经典问题，答案就是若最大值不超过总数一半，则能够全部匹配；否则，用所有的值去匹配最大值。根节点剩下的路径数为 $0$ 即合法。

AGC010D Decrementing

有趣博弈论，不是很难。

考虑如果没有第二步操作，那么这就是一个弱智题，容易发现我们的答案只与和的奇偶性有关。但是此时有了第二步操作就不一定了。

不过我们同样可以用同样的思路去考虑。我们首先有一个重要结论：只有除以 $2$ 是会影响结果的。因为除以任何其他的质因子都不会改变和的奇偶性。那么如果我们能够一直保证不会除以 $2$ ，那么和的奇偶性就不改变，那么上述结果就仍然成立。

接下来我们分情况讨论。若 $n$ 为偶数时，总和为奇数先手必胜。那么如果当前和为奇数，说明一定有奇数个 $1$ ，此时先手可以一直能选 $0$ 就选 $0$ ，这样后手永远无法使得所有数都变成 $0$ ，也就无法改变结果，此时先手必胜。而如果总和为偶数，说明一定有大于等于 $2$ 个 $1$ ，此时先手无论怎么操作都会落到和为奇数的情况，此时后手必胜。同理， $n$ 为奇数时，总和为偶数先手必胜，若总和就是偶数那么先手一定必胜，不过此时如果和为奇数不太一样。如果和为奇数，且仅有一个数为奇数时，先手可以选择将这个数减 $1$ 并使得所有数除以至少 $2$ 。这时候原来的和的规律被打破了，不过我们可以递归下去继续做，因为这个过程最多进行 $\log$ 次。

AGC009C Division into Two

直接 DP，设 $f_{i}$ 表示第一个集合最后一个球放 $i$ 的方案数。枚举转移点 $j$ ，那么这个点必定需要满足 $s_{i} - s_{j} \geq a$ ，且中间的所有 $s_{k} - s_{k - 1} \geq b$ 。容易发现满足这样条件的 $j$ 是一个区间。那么前缀和优化即可。

但是这样会出错。因为这样并没有保证 $j$ 前后的第二个集合之间的数距离 $\geq b$ 。我们发现这意味着存在 $s_{i} - s_{i - 2} < b$ ，那么这相邻的三个数之间一定存在两个数在相同集合内且距离 $< b$ 。如果我们钦定 $a > b$ ，那么如果有这种情况一定是无解的，所以我们可以先判掉这种情况，再做就行了。

AGC010F Tree Game

之前模拟赛考过的，炒冷饭了属于是。

考虑到我们肯定不会往比自己权值大的方向走，因为这样对手可以再走回来，走到最后一定是你死，那么我们就只会往大的边走。然后就是个简单博弈了。

AGC009D Uninity

高级题目。想不到怎么转化问题。

问题相当于要建一棵点分树，使得深度最小。我们考虑将每个点的最深深度写在这个点上，考虑这样的深度序列有什么性质。

发现：若有两个点 $c_{x} = c_{y}$ ，那么在 $x - y$ 的路径上一定存在一个点的深度大于 $c_{x}$ 。根据点分树的性质容易得出这点成立。而发现这是一个充要条件，因为这样我们可以每次找到深度最大的那个点作为点分树的分割点，显然能够得到一棵合法的树。

那么我们考虑贪心构造这个东西。我们采取能填就填的策略。那么我们记 $s_{u}$ 为子树 $u$ 中还没有出现大于其深度的点的深度集合。那么容易发现：

$\forall v \in s o n_{u}, c_{u} \notin s_{v}$ ；
$\forall v_{1}, v_{2} \in s o n_{u}, c_{u} > max {s_{v_{1}} \cap s_{v_{2}}}$ 。

那么只需要贪心的去维护即可。根据点分树的知识，容易知道深度不会超过 $\log$ ，那么这个集合我们可以状压维护。然后直接贪心做即可。

求得 $c_{u}$ 之后， $s_{u}$ 就是所有集合的并，删去所有小于 $c_{u}$ 的数，并加入 $c_{u}$ 。

AGC011C Squared Graph

AGC 好多这种构造图的题。

题目看着很抽象，我们这么去考虑：任意选两个点，让这两个点沿着图同时移动，问最少选多少点对进行这样的移动能够访问到所有点对。

那么我们先把原图按照连通块拆开。这样我们考虑所有的连通块对，不同的连通块对之间显然是互不影响的。考虑对每个连通块进行黑白染色。我们称一个连通块能黑白染色为好块。如果选择的两个点都在好块内，那么一次移动两个点所在的颜色同时改变，则两个颜色相等关系是不变的。同时，也容易构造出方案遍历所有的点对，于是这样的情况就需要两对点。而如果选择的期中一个点不在好块内，那么我们找到一个奇环一直绕，就能将黑白两个连通块连接了，于是就只需要一对点。需要注意一个点的连通块，这时候它哪里也移动不了，所以就是点数大小个点对了。

把所有 AGC 的 $\geq$ 紫的题全部加题单了，虽然我肯定也做不完，目标一个月做两个题单之类的吧。

link

想了想，这个做题纪要以周为单位吧，一周开一个博，好像不错的。要不要引流？好像本来也没人看，是不是没啥意义。

2023.9.7

不知道有没有啥可记的，接着 AGC 了。

AGC011D Half Reflector

事实证明还是得手模，好像手模发现一点性质这题就做完了。

我们发现，如果开头是 $A$ ，那么开头直接返回。否则，我们发现，这个球是可以一直到最后的。具体我们考虑球下一个是什么：

若为 $AA$ ，那么我们会在这两个装置上各反弹一次，变为 $BA$ ；
若为 $AB$ ，那么会直接过去，变为 $AA$ 。

发现，经过之后前一个字符永远都是 $A$ ，于是一定是往右走的。同时，发现每走一次，前一个字符会变成后一个字符的翻转，那么这个操作实际上就是整体移位加翻转。这个是很容易模拟的。

继续手模，发现一直进行这个操作后会变成 $BABA \dots BABA$ 或者 $ABABA \dots BABA$ 的形式，前者进行操作后不变，后者操作后只会更改第一个字符。那么我们可以暴力模拟前 $O (n)$ 次操作，然后剩下的操作次数直接模 $2$ 即可。

AGC011E Increasing Numbers

感觉有点诡异。

考虑贪心，每次选一个最长的上升序列 $X$ ，然后减去一个 $(X - 1) 999 \dots 99$ 的东西，这样会使得这个上升序列被删除，且后面的数加 $1$ 。正确性感性理解就是，如果进行调整，那么相当于给剩下的数增加一个上升序列，发现这样进行调整不能使得下一次选择的上升序列长度增加，所以后面全填 $9$ 是更优的。严谨证明不会。

加 $1$ 的过程就暴力加，加法器众所周知均摊 $O (1)$ 。需要特别注意一下连续的相同的数的情况，这时候虽然是上升但是不一定全选（减 $1$ 后可能不再上升）。

比较优美的做法：

一个上升数可以表示成 $9$ 个 $1111 \dots 111$ 的和（包括长度为 $0$ 的数），而这种数可以表示成 $\frac{10^{l e n} - 1}{9}$ ，那么如果这个数能够被表示成 $k$ 个上升数相加，那么就意味着这个数能够表示成 $9 k$ 个 $\frac{10^{l e n} - 1}{9}$ 的和，即 $n = \sum_{i = 1}^{9 k} \frac{10^{p_{i}} - 1}{9}$ ，即 $9 n + 9 k = \sum_{i = 1}^{9 k} 10^{p_{i}}$ ，那么我们就只需要判断 $9 n + 9 k$ 能否表示成 $9 k$ 个 $10^{p}$ 的和即可。

首先有显然的必要条件，就是各数位和不超过 $9 k$ ，而又因为和必须是 $9$ 的倍数（因为整个数是 $9$ 的倍数），于是发现这能够构成充分条件，具体就是我们可以用 $10$ 个 $10^{p - 1}$ 形成一个 $10^{p}$ ，这样能够用 $9 k$ 个数得到任意一个数位和为 $9 (k - 1)$ 的数，更小的同理。那么我们只需要判断数位和是否小于等于 $9 k$ 即可，直接暴力加法维护即可。

AGC011F Train Service Planning

首先我们发现，令第一辆车不停是不劣的。两辆车同时走不好考虑，我们考虑变换一下坐标系，让第一辆车不动，然后第二辆车的速度从 $1$ 变成 $2$ 。我们再将 $a_{i}$ 全部乘 $2$ ，就变成了第二辆车斜率为 $1$ 进行走。这样，我们要走的就是判断第二辆车如何走，能够使得不会在两站中间与第一辆车相遇，这也就是说 $0$ 坐标不会出现在第二辆车的行走路线中。设 $a_{i}$ 的前缀和为 $A_{i}$ ，且令当前停的总时长为 $x$ ，那么我们只需要满足 $0 \notin (a_{i} + x, a_{i + 1} + x)$ ，即 $x \in (- a_{i + 1}, - a_{i})$ 。我们要做的，就是选择一个合适的起点，使得 $x$ 增长的最少。那么我们可以维护从每个位置开始走所花费的最少时间，如果一个区间不能经过，那么就只能是这个区间的上一个位置往下走的，发现这相当于是一个区间覆盖等差数列，珂朵莉树维护即可。

AGC012C Tautonym Puzzle

简单构造。

考虑将整个数列分成两半，只允许出现左边与右面子序列相等的情况。

这种题很常见的去构造 $\times 2$ 与 $+ 1$ 。发现在左右两个序列后同时加一个数就会使方案数 $\times 2$ ，在开头结尾各放一个数就会使方案数 $+ 1$ ，然后就没了。

今天摆的有点严重了。寄。

2023.9.8

困困困困困困困困困困困困

发现 tetr.io 还是很好玩的。上 10 级了，可以挑战 tetra league 了哈哈。

中午尝试打打 WTF 玩。rating 下限 2000 分，这题是不是难度会巨大高啊。感觉会掉大分。（事实证明啥都不会，直接摆烂）

AGC012D Colorful Balls

我们将能进行交换的两个球连边，这样每个连通块内的球可以任意交换顺序。那么显然我们只需要知道联通情况就行了，然后计算就是简单的多重组合数。

考虑快速建图。发现我们只需要将每个球与其能相连的最小重量的球相连即可（同颜色间最小的与不同颜色最小的），连最小的肯定不劣。

AGC013C Ants on a Circle

应该说是挺套路的题。

首先有重要观察：蚂蚁之间的相对位置关系显然不会改变。

但是反弹这件事情并不好考虑，我们考虑将其转化为：蚂蚁之间不反弹，而是交换他们的编号。这样我们容易发现每一只蚂蚁的最终位置是极其容易计算的，只需要知道他最后的编号是什么即可。

而又由于相对位置关系不会改变，那么当两只蚂蚁交换编号时，这两只蚂蚁的编号一定是 $x, x + 1$ ，交换后变成 $x + 1, x$ 。那么也就是说，我们其实只需要知道每一只蚂蚁与多少只蚂蚁相交过就能推出他的标号了。

然后就是发现同时动非常难考虑，考虑让与蚂蚁反向的那些直接静止，只让它自己动，这样我们就是要找区间内有多少只蚂蚁了，这个是很容易计算的，只需要知道经过了多少个周期再二分找到分界点即可。注意参考系变换之后速度为 $2$ ，经过的区间长度为 $2 T$ 。

AGC013D Piling Up

考虑枚举最一开始的球有 $x$ 个黑球。发现每一轮都取出两个球并放入两个球，所以球的总数恒为 $n$ 。那么我们可以考虑直接对这东西做格路计数。这个东西是可以合并起来做的，所以直接做就是 $O (n m)$ 。但是这样做同一条格路可能被计算多次，为了避免重复计算钦定格路最小值必须等于 $0$ ，这个直接经典容斥，拿 $n$ 的答案减 $n - 1$ 的答案。

AGC013F Two Faced Cards

感觉非常有难度的题啊，完全不会了。想模拟费用流，但是想了想觉得啥都不对然后就扔了。果然我还是不会贪心，感觉贪心好难。

这是一个类似于二分图匹配的问题，根据 Hall 定理容易转化成以下问题：

有一个序列 $A$ ， $n$ 个二元组 $(a_{i}, b_{i})$ ，每个二元组选择两个数中的一个，使得 $A [a_{i}, \infty)$ 区间 $+ 1$ ，对于每一个 $c_{i}$ 令 $A [c_{i}, \infty)$ 区间 $- 1$ ，问最多选择多少个 $a_{i}$ ，使得任意位置 $A_{i} \geq 0$ 。

对于每次插入一个二元组，我们先直接枚举选的哪一个，那么就相当于对 $A$ 后缀 $+ 1$ ，我们不妨改条件为：

问最多选择多少个 $a_{i}$ ，使得 $A (- \infty, k) \geq 0, A [k, \infty) \geq - 1$ 。

我们先钦定全部都选 $a_{i}$ ，那么如果要将一个二元组改成 $b_{i}$ ，那么就是对 $[b_{i}, a_{i})$ 区间 $+ 1$ （若 $b_{i} \geq a_{i}$ 显然选 $b_{i}$ 没有意义），那么问题变成了：

有一个序列 $A$ ，给定 $n$ 个区间 $[b_{i}, a_{i})$ ，选择最少个区间进行 $+ 1$ ，使得 $A (- \infty, k) \geq 0, A [k, \infty) \geq - 1$ 。

接下来我们可以证明一个性质：对于最大的 $A_{i} < - 1$ ，包含 $i$ 的区间中左端点最靠左的区间 $I$ 一定在最优解中。

证明：

假设存在一组最优解中没有 $I$ ，而覆盖 $i$ 的右端点最靠左的区间为 $J$ ，那么：

若 $i < k$ ，即需要满足 $A_{i} \geq 0$ ，那么至少存在两个区间覆盖了 $i$ ，那么 $J$ 的右端点必定被两个区间覆盖，而又因为 $i$ 是最大的 $A_{i} < - 1$ 的位置，那么说明 $A (i, \infty] \geq - 1$ 的，这些位置只需要被一个区间覆盖即可，那么此时我们可以将区间 $J$ 换为 $I$ ，条件仍然能够满足。

若 $i \geq k$ ，即需要满足 $A_{i} \geq - 1$ ，那么 $i$ 往右的所有位置已经满足条件了，此时将左端点设为更小的区间肯定不劣。

那么我们就得到了一个贪心的算法：每次找到 $A_{i} < - 1$ 的最靠右的位置，然后将包含这个位置的左端点最靠左的区间选中，一直进行这个操作即可。

那么进行完这个操作之后，所有的 $A_{i} \geq - 1$ ，我们需要将某个前缀的 $- 1$ 全部覆盖，这也是可以直接贪心的，每次找到最靠左的 $- 1$ ，选择包含这个位置的右端点最靠右的区间即可。发现这个过程正好是覆盖的一个前缀，所以我们可以对所有的 $k$ 的答案直接全部处理出来。

具体维护：首先离散化，然后每次查询的端点都是单调递减的，而所有的区间都一定包含当前点，所以可以用堆来维护修改区间的左端点，可以快速计算当前点被区间加了多少次。第二部分和第一部分的操作本质是相同的。

2023.9.9

上午水哥把网关了。然后就打模拟赛完了。模拟赛题有点水了。

然后下午水哥问我怎么跟着打比赛了，我可以不跟着打的，我说我知道我可以不打，但是网关了闲的没事就打了。

~~今天当给我自己放假了。~~

下午讲了个题，然后摆了一会，去班里吃蛋糕（~~为信奥准备的送别礼~~）

把昨天那个 AGC F 写了。然后真的困了，摆烂了。

打算先把板刷 AGC #1 做完，然后把之前在南外的遗留问题解决。

2023.9.10

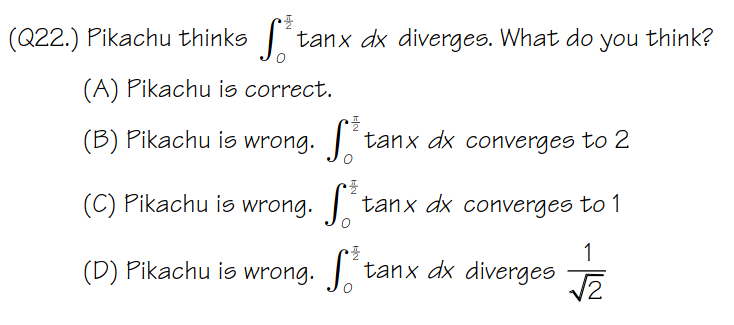
I think: Pikachu 都会高数，好可怕。

\begin{aligned} \sum_{i = 1}^{n} i^{k} & = \sum_{i = 2}^{n + 1} (n + 2 - i)^{k} \\ \equiv \sum_{i = 2}^{n + 1} (- i)^{k} & (\mod n + 2) \\ \equiv - \sum_{i = 2}^{n + 1} i^{k} \end{aligned}

假设 $\sum_{i = 1}^{n} i^{k} \equiv 0 (\mod n + 2)$ ，那么 $\sum_{i = 1}^{n} i^{k} \equiv \sum_{i = 2}^{n + 1} i^{k}$ ，即 $1^{k} \equiv (n + 1)^{k} \equiv (- 1)^{k} \equiv - 1$ ，而这个显然不成立，所以证完了。

我会做初中 MO 题了，哈哈。

今天电脑第三次假死了，不太懂原理，反正就是突然电脑黑屏然后自动注销，登录不了，开虚拟终端随机杀几个进程就好了。这次杀了半天没发现问题，杀了个 clash 好了。被 clash 刺杀了属于是。

AGC014D Black and White Tree

观察样例，可以发现：若一个点有两个儿子为叶子节点，那么先手直接操作这个，后手操作完之后一定剩下一个儿子节点不被操作，此时操作一定胜利。

这意味着，只要先手操作一个点，这个点有儿子为叶子节点，那么后手必须要操作这个叶子节点。

那么我们就可以按照这样的策略去做：每次选一个叶子，将其父亲染色，这样后手一定会把这个叶子删掉。假如对于某一个点，它的所有子树都被染色了，那么这个点就不能被染色，只要有一个子树没有被染色那么它就必须被染色。那么我们只需要知道，是否存在一个根节点 $x$ ，以他为根进行这样的过程，是否能有大于等于 $2$ 个子树没有被染色。这个容易换根 DP 做出。

AGC014E Blue and Red Tree

还是很显然的，策略就是能删就删。只要一条边仅被覆盖了一次那么就可以直接删对应的边，否则就不能删。直接树剖线段树维护覆盖次数即可。

简单的实现细节：维护这个边被哪条路径覆盖的时候，可以维护所有覆盖它的路径的异或和，这样只剩一条边的时候这个异或和就是覆盖路径的编号。

AGC014F Strange Sorting

超级大结论题。

Observation：对于一开始的序列来说，如果把数字 $1$ 删去，那么接下来的过程中剩下的数的相对位置不会发生改变。

这个是显然成立的。那么这意味着，如果我们能够知道删去 $1$ 的序列需要多少次操作，并且知道这么多次操作之后 $1$ 是否在开头的位置，我们就能够知道整个序列需要多少次操作。那么不难发现这个问题是可以通过这种方式递归解决的。

那么我们就着重来考虑这个问题：如何求出将 $[2, n]$ 排序后 $1$ 是否在开头。

设 $[2, n]$ 在进行 $T$ 次操作后有序，如果 $T = 0$ ，那么显然可以直接判断，所以我们只考虑 $T \geq 1$ 的情况。

Lemma 1：对于 $[2, n]$ 的序列，进行 $T - 1$ 次操作后，开头数字 $f > 2$ 。
Proof：若 $f = 2$ ，那么 $f$ 一定是 high 元素，进行一次操作之后一定会到后面的位置，这与 $T$ 次操作后排好序矛盾。

那么这意味着，开头的数字一定不是 $2$ ，那么此时我们考虑 $f, 1, 2$ 之间的位置关系，如果 $1$ 在 $f$ 与 $2$ 中间，那么在第 $T$ 次操作后 $1$ 就在开头，否则就不在开头。

但是我们并不能得知 $T - 1$ 次操作后 $f, 1, 2$ 的位置关系。此时我们有一个更强的结论：若 $f, 1, 2$ 在初始序列中的循环位置等于 $(f, 1, 2)$ ，那么 $T - 1$ 次操作的时候顺序一定是 $f, 1, 2$ ，即 $T$ 次操作的时候 $1$ 一定在开头。（循环顺序指这三个数的顺序与 $(f, 1, 2)$ 循环同构，即 $(f, 1, 2) / (1, 2, f) / (2, f, 1)$ ）

为了证明这一结论，我们只需要证明，进行任意一次操作之后， $f, 1, 2$ 之间的循环顺序不变。

Lemma 2：在 $[2, n]$ 的序列中， $f$ 为 high 元素，当且仅当 $f$ 在开头。
Proof：反证法，假设某一时刻 $f$ 不是开头但是成为了 high 元素，那么进行一次操作后它前面的 high 元素 $g < f$ 会与 $f$ 紧挨在一起，而只有 $g$ 成为 low， $f$ 成为 high 的情况下两者会分开。而出现这种情况的前提是 $f$ 前面还有别的数为 $h i g h$ ，所以这种情况发生后 $f$ 又会与另外一个数紧挨在一起，所以 $f$ 不可能成为第一个数。

有了这个结论，我们可以直接讨论任意时刻下 $f, 1, 2$ 的顺序了。注意到，循环顺序发生改变，当且仅当按位置关系下三个数分别是 high, low, high 或 low, high, low。

若 $1$ 在开头，那么：
- 若 $2$ 为第二个数，那么 $1, 2$ 为 high， $f$ 为 low，循环顺序不变；
- 若 $f$ 为第二个数，那么 $1, f$ 为 high， $2$ 为 $l o w$ ，循环顺序不变；
- 否则 $1$ 为 high， $2, f$ 为 $l o w$ ，循环顺序不变；
若 $2$ 在开头，那么 $2$ 为 high， $1, f$ 为 low，循环顺序不变；
若 $f$ 在开头，那么 $f$ 为 high， $1, 2$ 为 low，循环顺序不变；
否则 $1, 2, f$ 均为 low，循环顺序不变。

那么做法就很简单了，我们只需要判断最一开始 $f, 1, 2$ 的顺序是否符合 $(f, 1, 2)$ 即可。那么我们利用这一性质递归去求解即可。

AGC015D A or...or B Problem

貌似是去年省选模拟赛考过的题？当时 AT 交的代码 WA 了，我就直接咕了。

其实也是不难的。首先两个数的 LCP 肯定是没有用的，直接删掉。

首先我们知道，得到的数一定全部 $\geq l$ ，设 $r$ 的最高位为 $x$ ，那么所有数一定 $< 2^{x + 1}$ 。那么考虑哪些数能取到。设 $l$ 的最高位为 $y$ ，那么发现，对于任意 $i \in (y, x)$ ，以 $i$ 为最高位的所有数都是能够取到的，这说明最高位为 $y$ ，且 $(y, x)$ 内不为 $0$ 的所有数都是可以取到的，那么我们就仅需要考虑 $(y, x)$ 内全部为 $0$ 的数有哪些能够取到。首先发现如果 $r$ 中的第二高位 $z > y$ ，那么所有数都是可以取到的。那么如果 $z \leq y$ ，那么相当于问我们有 $[0, r - 2^{x}] \cup [l, 2^{z})$ 中的所有数能组成多少数。由于或起来一定大于本身，所以 $[l, 2^{y})$ 内的数只能形成它本身，所以只考虑 $[0, r - 2^{x}]$ ，而这个也是显然的，这些数可以形成 $[0, 2^{z})$ 中的所有数（ $z$ 即为 $r - 2^{x}$ 最高位），那么只需要判断一下这两个区间是不是有交，然后把不合法的数减掉即可。

是不是本来说这个博一周开一个的。算了发现 AGC #1 要做完了，把剩下的更完了再开新博吧。做完 AGC #1 颓会 whk。

2023.9.11

~~今天是 911。~~ 今天大概能把 AGC #1 做完了吧。打算做完剩下几道题 whk 一会。

昨天把学考报了，感觉 12 月就要考五科我完全没学的科，有点恐怖。所以我还是应该把高一 whk 补一下吧。要不然五科全过不了就比较傻逼了。

希望我能过两科！

怎么今年精英培训 50 个人。那这下子我好像还能报，把高二去掉正好 49 名，呃呃。那要报名吗。

AGC016D XOR Replace

不算很难。考虑将一个数变成全局异或和，相当于将这个数异或上除了这个数以外的所有数，这会使得全局异或和变成选择的这个数。那么发现，这个操作实际上是将某个数与全局异或和进行了交换。那么这其实就变成了一个排序问题。

我们首先将所有 $a_{i} = b_{i}$ 的地方全部删掉。假如原序列是一个排列，这是经典的问题，答案就是 $n + 置换环数量$ 。但是此时是一个任意序列，而且初始临时变量也有一个值，所以需要额外的思考。其实也并不难，因为每个数必须成对出现（除了操作前与操作后的全局异或和），表示成图相当于每个点入度出度相等，那么每个连通块都是存在欧拉回路的，所以如果不考虑初始值答案仍然是 $m + 连通块数量$ 。不过此时出现了一个初始值，那么我们可以直接把这个数也放到图里，容易发现操作前后的全局异或和一定在同一个连通块内，而这个连通块是不需要通过一次操作进入的，于是我们给答案减掉 $1$ 就是答案。

AGC015F Kenus the Ancient Greek

确实绷不住了，翻了五六篇题解终于凑出了这个证明。题蛮酷的，但是这题是真的没人证明啊我真的绷不住了。

不过还是证不出来官方题解里面那个 $F_{k + 2}$ 的上界，不过能证出来一个较松的，结论是一样的，不管了。

首先考虑如何求最大的值是多少，这个是很经典的，众所周知用斐波那契数可以将欧几里得算法次数卡到最大，所以我们只需要找出最大的 $F_{k} \leq A, F_{k + 1} \leq B$ ，那么最大的 $f (x, y)$ 就是 $k$ 。我们设 $A, B$ 内最大的 $f (x, y)$ 为 $g (x, y)$ 。

关键在于如何计数。首先减少有用的数对，我们只关心所有 $f (x, y) = g (x, y)$ 的数对，若 $f (x, y) < g (x, y)$ 那么这个数对显然永远不会被统计到。我们称这样的数对 $(x, y)$ 为对子。若 $f (x, y) = k$ ，我们称它为 $k$ 对子。容易发现，对子 $k$ 一定满足 $x \geq F_{k}, y \geq F_{k + 1}$ （假设 $x < y$ ）。

但是对子的数量仍然是很多的，例如所有 $(1, m), m \geq 2$ 都是对子。而我们发现，这些对子的形式是类似的，它们在进行一步之后都会变为 $(0, 1)$ 。那么我们将这些进行一步之后能够得到的对子叫做基对，其中令 $f (x, y) = k$ 的基对叫 $k$ 基对。可以发现，这样的基对数量是很少的。并且我们可以证明，对于所有的 $k$ 基对，都有：

$(x, y)$ 是 $k$ 对子；
$x, y \leq F_{k + 2} + F_{k - 1}$ 。

前者原因是显然的。考虑证明后者。

假设存在一个 $k + 1$ 对子 $(x, p x + y)$ ，进行一步操作后得到的 $k$ 对子 $(y, x)$ 不是一个基对，那么必定有 $x > F_{k + 2} + F_{k - 1}$ 。由于 $f (y, x) = k$ ，那么 $y \geq F_{k}$ ，这意味着 $p x + y > F_{k + 2} + F_{k - 1} + F_{k} = F_{k + 3}$ ，即 $x > F_{k + 2}, p x + y > F_{k + 3}$ ，这与 $(x, p x + y)$ 为 $k + 1$ 对子矛盾。所以任意一个 $k + 1$ 对子进行操作后一定得到一个 $k$ 基对。

那么 $k$ 基对有多少呢？事实上， $k$ 基对有恰好 $k + 1$ 个（若只算 $x < y$ 的）。接下来我们用归纳法证明这一点。

首先考虑 $k = 1$ ，基对肯定都是 $(1, m)$ 的形式，而这些基对能得到的最小的 $2$ 对子为 $(m, m + 1)$ ，若 $m \geq 3, m + 1 \geq 5$ 那么这就不是 $2$ 对子了，所以 $m$ 最大为 $3$ 。于是 $k = 1$ 的基对有 $(1, 2), (1, 3)$ 两个。（不考虑这么多直接把 $(1, 4)$ 也看做基对其实也是没有问题的，不会影响后面的证明。）

考虑由 $k$ 基对递推出 $k + 1$ 基对。由于基对也是对子，基对在操作后一定也是基对，所以我们只需要从每一个 $k$ 基对考虑能够得到哪些 $k + 1$ 对子是基对即可。也就是说，如果有一个 $k$ 基对 $(y, x)$ ，我们只需要考虑哪些 $(x, p y + x)$ 是 $k + 1$ 基对即可，即哪些 $p x + y \leq F_{k + 3} + F_{k}$ 。

首先，对于每一个 $(x, y)$ ，一定存在 $(y, x + y)$ 。 $k = 1$ 时可以验证， $k$ 更大时由于存在 $(y mod x, x)$ 的 $k - 1$ 基对，一定有 $x \leq F_{k + 1} + F_{k - 2}$ ，所以 $x + y \leq F_{k + 3} + F_{k}$ 就是显然的。

那么存不存在 $(y, x + 2 y)$ 呢？接下来我们证明，除了 $(1, 2)$ 与由 $(1, 2)$ 得来的 $k$ 基对 $(F_{k}, F_{k + 1})$ 这个基对以外，其它的所有基对都不能推出 $(y, x + 2 y)$ 的基对。

首先我们发现，除了 $(F_{k}, F_{k + 1})$ 以外，所有的 $k$ 基对 $(x, y)$ 一定都满足 $x \geq F_{k} + F_{k - 2}, y \geq F_{k + 1} + F_{k - 1}$ ，由 $(x, y) \to (y, x + y)$ 得出的新基对容易验证满足这个限制。考虑这样的基对能否生成 $(y, x + 2 y)$ 。由于 $x + 2 y \geq F_{k} + F_{k - 2} + 2 F_{k + 1} + 2 F_{k - 1} = F_{k + 3} + F_{k + 1} > F_{k + 3} + F_{k}$ ，于是显然这样生成的数对是不合法的，故得证。

而对于 $(F_{k}, F_{k + 1})$ 的基对，我们是可以通过 $(x, y) \to (y, x + 2 y)$ 得到新的基对的，即 $(F_{k}, F_{k + 1}) \to (F_{k + 1}, F_{k} + 2 F_{k + 1} = F_{k + 3})$ 。而对于这个新的 $k + 1$ 基对 $(F_{k + 1}, F_{k + 3})$ ，它也是不能得到 $(y, x + 2 y)$ 基对的（容易验证，略），而得到的新基对 $(y, x + y)$ 也是满足上述的 $x^{'} \geq F_{k^{'}} + F_{k^{'} - 2}, y^{'} \geq F_{k^{'} + 1} + F_{k^{'} - 1}$ 性质的，于是我们证明了，对于任意一个 $k$ ，仅有 $(F_{k}, F_{k + 1})$ 会生成一个新的基对 $(F_{k + 1}, F_{k + 3})$ ，所有基对均由 $(x, y) \to (y, x + y)$ 生成一个对应的基对，于是这就表明 $k$ 基对一共只有 $k + 2$ 个。

不等式证明，真你妈阴间，放缩到吐了。

那么我们就可以简单的在 $O (\log^{2} V)$ 的复杂度内找出所有的基对。询问时，我们只需要考虑枚举 $k - 1$ 基对 $(x, y)$ ，然后看有多少 $(y, x + p y)$ 即可，这个统计答案是十分简单的。注意特判 $k = 1$ 。复杂度 $O (\log^{2} V + T \log V)$ 。

AGC016F Games on DAG

个人感觉很有意思。

首先题目显然是一个组合游戏，那么两个棋子的 SG 值不相等则先手必胜。

那么我们相当于要对 SG 值进行 DP。题目中的条件很容易让我们往拓扑序的方向去想，但是如果按照拓扑序依次确定 SG 值，需要记录的东西太多，无法接受。

考虑按照 SG 值来分层 DP。我们首先确定哪些点的 SG 值是 $0$ ，然后哪些是 $1$ ，哪些是 $2$ ，依次类推。发现一个重要性质：如果当前剩余的点集中没有连向某个 SG 为 $0$ 的点的边，那么这个点的 SG 值就必定为 $0$ 。这意味着，我们可以记 $f_{S, i}$ 表示 $S$ 点集中的所有点的 SG 值全部大于等于 $i$ 的方案数，每次选出一个 SG 值为 $i$ 的点集，让剩下的点全部至少向这个点集连一条边，然后继续去做。 $1, 2$ 点的 SG 值不相等，那么枚举点集的时候钦定 $1, 2$ 不能同时出现在这个集合中即可。预处理出点集向点集连边的方案，总复杂度 $O (3^{n} n)$ 。

AGC001-016 完结撒花 🎉

这篇博到这里吧，开篇新博了。

posted @ 2023-08-31 21:37 APJifengc 阅读(449) 评论(13) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 2023.10 做题纪要 #3

· 2023.10 做题纪要 #1

· 9月杂题选做

· 2023 7 月总结

· Solution Set -「AGC 010~012」C~F

阅读排行：
· 无需6万激活码！GitHub神秘组织3小时极速复刻Manus，手把手教你使用OpenManus搭建本
· Manus爆火，是硬核还是营销？
· 终于写完轮子一部分：tcp代理了，记录一下
· 别再用vector＜bool＞了！Google高级工程师：这可能是STL最大的设计失误
· 单元测试从入门到精通