【学习笔记】万能欧几里得算法

类欧几里得算法，是一类可以通过辗转相除的方式递归解决的问题，由于其复杂度分析与欧几里得算法一致，所以称为类欧几里得算法。其中，类欧最常见的形式是直线下整点数问题，即求 $y = \left\lfloor\dfrac{px+r}{q}\right\rfloor$ 这个函数的相关问题，如 $\sum y$，$\sum y^2$，$\sum xy$。而传统的类欧推导方法多数繁琐复杂，式子长，难推导且难记。这时候，我们有一个算法，叫万能欧几里得算法，他将上述问题进行抽象化，并给出了这类问题的一个通用解法。不过，两者的思想是完全相同的，所以我们还是先介绍传统的类欧算法。

考虑最基础的问题：求 $\displaystyle \sum_{x=1}^n \left\lfloor\dfrac{px+r}{q}\right\rfloor$。

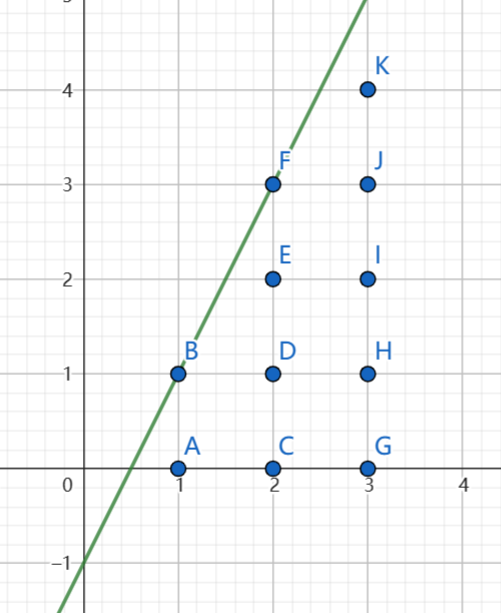
我们不去从这个式子的角度去考虑这个问题，而是从图像的角度去考虑。我们不妨画出 $y=\dfrac{px+r}{q}$ 这个图像，那么我们求的就是一个区域内的整点数。

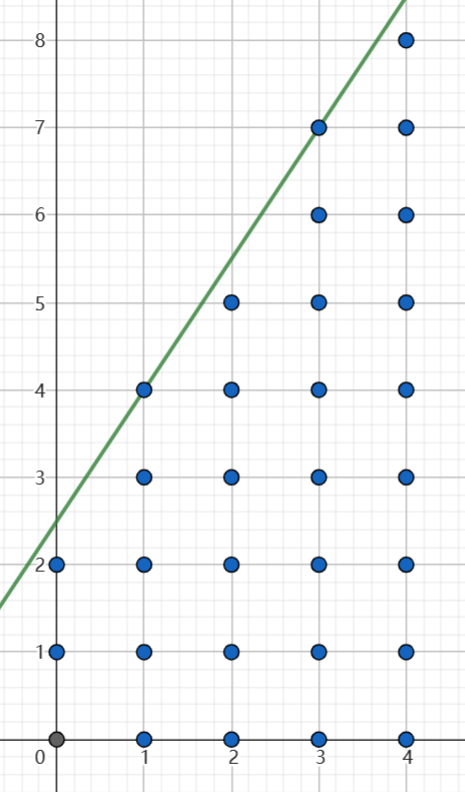
如图是 $y=\frac{3x+5}{2}$ 的情况。

我们通过两种操作来计算这些点数：

截距大于等于 $1$ 时，将下方的点的数量统计出来。
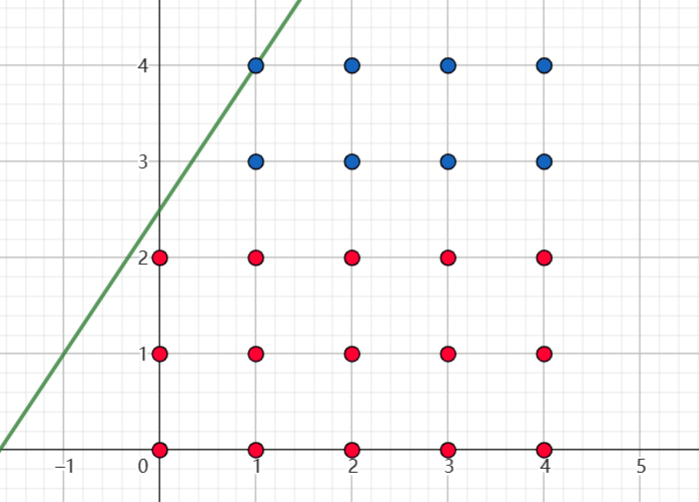
当斜率大于等于 $1$ 时，将整数斜率下的点的数量统计出来。
整数斜率下的点数是容易统计的，因为这就是一个等差数列求和。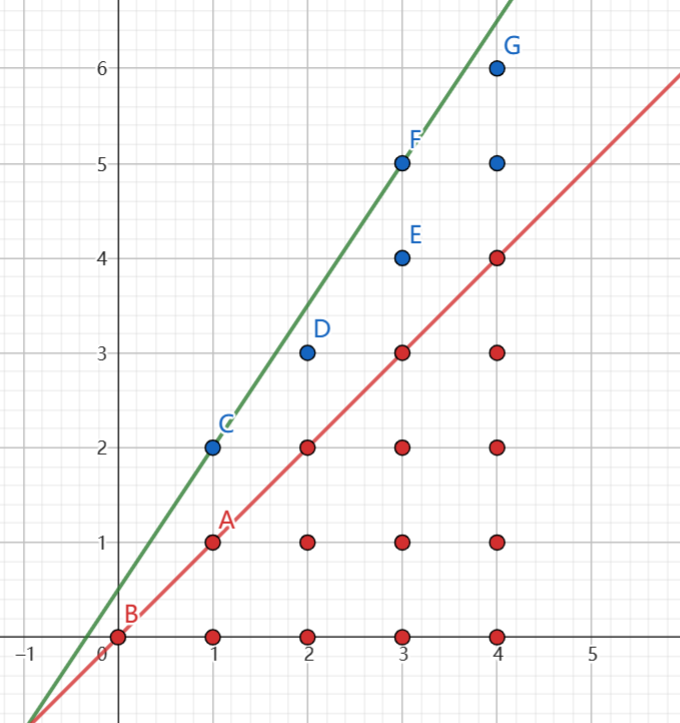
此时，截距与斜率均小于 $1$，我们将图像的 $x, y$ 轴翻转过来，这样我们又递归变成了一个求斜率小于 $1$ 的子问题。

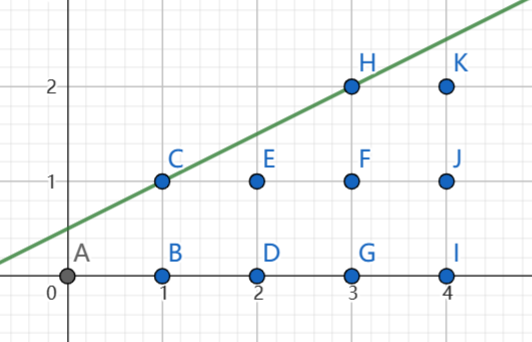
变为：

我们设斜率为 $\frac{p}{q}$，容易发现，第二步的操作实际上将 $\frac{p}{q} \to \frac{p \bmod q}{q}$。第三步的操作实际上将 $\frac{p}{q} \to \frac{q}{p}$。容易发现，这实际上是在对 $(p, q)$ 二元组做欧几里得算法。于是，这样做的递归次数就是 $O(\log \max\{a, b\})$。

万能欧几里得算法的思想与上述算法的思想是一模一样的。不过，我们用另外一种方法抽象这个问题：

给定二维坐标系上的一次函数 $y=\dfrac{px+r}{q}$。我们维护一个向量 $v$，考虑这个函数每次向右穿过网格的竖线时，给 $v$ 乘上一个矩阵 $R$；每次向上穿过网格的横线时，给 $v$ 乘上一个矩阵 $U$。若恰好经过一个整点，那么先乘 $U$ 再乘 $R$。若 $x \in [1, n]$，求最后的向量 $v$。

例如，我们要计算 $\sum y$，我们可以通过维护一个向量 $[y, \sum y, 1]$，那么每次我们向上穿过网格时，$y$ 会加 $1$，即：

\[U = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 1 & 0 & 1\\ \end{bmatrix} \]

每次向右穿过网格时，$\sum y$ 会加 $y$，即：

\[R = \begin{bmatrix} 1 & 1 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{bmatrix} \]

拿最一开始的东西举例子，我们要求的就是 $[0\ \ 0\ \ 1]\ UURUURURUURUR$。

首先，问题相当于在说，求在第 $i$ 个 $R$ 前面，有 $\left\lfloor\dfrac{px+r}{q}\right\rfloor$ 个 $U$，一共有 $n$ 个 $R$，且最后一个为 $R$ 的矩阵乘积。

那么，我们类比类欧的做法，解决这个问题。

我们先定义函数 $\mathrm{euclid}(p, q, r, n, U, R)$ 为上述问题的答案。

若 $r \ge q$，那么就先把前面的 $\left\lfloor\dfrac{r}{q}\right\rfloor$ 个 $U$ 乘起来，即：

\[\mathrm{euclid}(p, q, r, n, U, R) = U^{\lfloor\frac{r}{q}\rfloor} \mathrm{euclid}(p, q, r \bmod q, n, U, R) \]
若 $p \ge q$，那么每个 $R$ 前至少有 $\left\lfloor\dfrac{p}{q}\right\rfloor$ 个 $U$，我们可以把这些 $U$ 和 $R$ 合并起来。考虑这样之后，每个数前面剩下的数有：

\[\begin{aligned} &\left\lfloor\frac{px+r}{q}\right\rfloor - x \left\lfloor\frac{p}{q}\right\rfloor\\ =&\left\lfloor\frac{px+r}{q}\right\rfloor - \frac{x(p - p\bmod q)}{q}\\ =&\left\lfloor\frac{px+r - x(p - p\bmod q)}{q}\right\rfloor\\ =&\left\lfloor\frac{(p\bmod q) x + r}{q}\right\rfloor \end{aligned} \]
也就是说：

\[\mathrm{euclid}(p, q, r, n, U, R) = \mathrm{euclid}(p \bmod q, q, r, n, U, U ^ {\lfloor\frac{p}{q}\rfloor}R) \]
否则，我们要翻转 $x, y$ 轴。

考虑第 $y$ 个 $U$ 前面有多少 $R$，容易发现这等于满足 $y > \left\lfloor\dfrac{px+r}{q}\right\rfloor$ 的最大整数 $x$。推式子：

\[\begin{aligned} y &> \left\lfloor\dfrac{px+r}{q}\right\rfloor\\ y &\ge \left\lfloor\dfrac{px+r}{q}\right\rfloor + 1\\ y &\ge \left\lfloor\dfrac{px+r + q}{q}\right\rfloor\\ y &\ge \left\lceil\dfrac{px+r + 1}{q}\right\rceil\\ y &\ge \dfrac{px+r + 1}{q}\\ yq - r - 1 &\ge px\\ x &\le \frac{qy - r - 1}{p}\\ x &\le \left\lfloor\frac{qy - r - 1}{p}\right\rfloor \end{aligned} \]
设 $m$ 为原来 $U$ 的数量，即 $m = \left\lfloor\dfrac{pn+r}{q}\right\rfloor$。于是，我们可以得到翻转后 $(p, q, r, n) \to (q, p, -r-1, m)$。但是，首先 $r$ 为负数我们是处理不了的，其次最后一个矩阵不一定是 $R$，也不符合定义。

首先第一个问题，我们可以将第一段 $U^i R$ 去掉再往下递归。这一段的 $U$ 的数量为 $\left\lfloor\dfrac{q - r - 1}{p}\right\rfloor$。

第二个问题，我们同样把最后一段 $U^i$ 去掉再往下递归。这一段的 $U$ 的数量为 $n - \left\lfloor\dfrac{qm - r - 1}{p}\right\rfloor$。

和前面类似的推导，我们能得到现在第 $x$ 个 $R$ 前面有 $\left\lfloor\dfrac{q(x+1) - r - 1}{p}\right\rfloor - \left\lfloor\dfrac{q - r - 1}{p}\right\rfloor = \left\lfloor\dfrac{qx + (q - r - 1) \bmod p}{p}\right\rfloor$。

那么现在还剩下 $m-1$ 个 $R$，所以有：

\[\mathrm{euclid}(p, q, r, n, U, R) = R^{\lfloor\frac{q-r-1}{p}\rfloor}U\mathrm{euclid}(q, p, (q-r-1) \bmod p, n, R, U) R^{n - \lfloor\frac{qm - r - 1}{p}\rfloor} \]
当然有点边界情况，如果 $m=0$ 的时候有：

\[\mathrm{euclid}(p, q, r, n, U, R) = R^n \]

假如一次乘法的复杂度为 $T$，那么我们能得到复杂度为 $O(T \log \max(p, q))$。快速幂的部分看起来需要多一个 $\log$，但是实际上我们发现，每次 $(p, q) \to (q, p \bmod q)$ 的过程中，我们进行了三次快速幂，复杂度分别为 $O(\log \frac{p}{q}), O(\log \frac{q}{p \bmod q}), O(1)$，通过将底函数拆掉容易得到。而由于 $(p, q)$ 是辗转相除的过程，容易发现所有的 $\frac{p}{q}$ 的乘积为 $O(p)$ 的，第二个一样。所以，这样做的总复杂度为 $O(T \log \max(p, q))$。

实际上矩阵是一个例子，我们只需要设计一个元，这个元有乘法运算，且乘法运算有结合律，那么就可以用这个算法解决。具体来说，我们可以把这个过程想象成一个分治的过程，只需要按照序列分治的方法设计状态即可。

先放一下主体部分的代码：

struct Node {
    Node operator*(Node b) {
        // ...
    }
};
Node pow(Node a, long long b) {
    Node ans;
    while (b) {
        if (b & 1) ans = ans * a;
        a = a * a;
        b >>= 1;
    }
    return ans;
}
Node euclid(long long p, long long q, long long r, long long n, Node U, Node R) {
    if (!n) return Node();
    if (r >= q) return pow(U, r / q) * euclid(p, q, r % q, n, U, R);
    if (p >= q) return euclid(p % q, q, r, n, U, pow(U, p / q) * R);
    long long m = ((__int128_t) p * n + r) / q;
    if (!m) return pow(R, n);
    return pow(R, (q - r - 1) / p) * U * euclid(q, p, (q - r - 1) % p, m - 1, R, U)
         * pow(R, n - ((__int128_t) q * m - r - 1) / p);
}

那么我们用具体问题来分析怎么设计状态。

P5170 【模板】类欧几里得算法

我们要求的是 $\sum y, \sum y^2, \sum xy$。

考虑如何合并两个区间。

设 $X_ {l/r}, Y_{l/r}$ 为左/右区间的 $x / y$ 的最大值，那么：

对于 $\sum y$ 来说，有 $\sum y = \sum y_l + \sum (y_r + Y_l) = \sum y_l + \sum y_r + X_r Y_l$；

对于 $\sum y^2$ 来说，有 $\sum y^2 = \sum y_l^2 + \sum(y_r + Y_l)^2 = \sum y_l^2 + \sum y_r^2 + 2Y_l \sum y_r + X_r Y_l^2$；

对于 $\sum xy$ 来说，有 $\sum xy = \sum x_l y_l + \sum (x_r + X_l)(y_r + Y_l) = \sum x_l y_l + \sum x_r y_r + Y_l \sum x_r + X_l \sum y_r + X_r X_l Y_l$；

发现我们还要维护一个 $\sum x$，有 $\sum x = \sum x_l + \sum(x_r + X_l) = \sum x_l + \sum x_r + X_l X_r$。

那么我们根据这个，维护 $X, Y, \sum x, \sum y\ ,\sum y^2, \sum xy$ 即可。

注意万欧求的是 $[1, n]$ 的和，此题要求 $[0, n]$，所以要把 $x=0$ 的答案加上。

#include <bits/stdc++.h>
using namespace std;
const int P = 998244353;
struct Node {
    long long x, y, sumx, sumy, sumy2, sumxy;
    Node() : x(0), y(0), sumx(0), sumy(0), sumy2(0), sumxy(0) {}
    Node operator*(Node b) {
        Node a = *this, c;
        c.x = (a.x + b.x) % P;
        c.y = (a.y + b.y) % P;
        c.sumx = (a.sumx + b.sumx + a.x * b.x) % P;
        c.sumy = (a.sumy + b.sumy + a.y * b.x) % P;
        c.sumy2 = (a.sumy2 + b.sumy2 + 2 * a.y * b.sumy + b.x * a.y % P * a.y) % P;
        c.sumxy = (a.sumxy + b.sumxy + a.y * b.sumx + a.x * b.sumy + b.x * a.x % P * a.y) % P;
        return c;
    }
};
Node pow(Node a, int b) {
    Node ans;
    while (b) {
        if (b & 1) ans = ans * a;
        a = a * a;
        b >>= 1;
    }
    return ans;
}
Node euclid(long long p, long long q, long long r, long long n, Node U, Node R) {
    if (!n) return Node();
    if (r >= q) return pow(U, r / q) * euclid(p, q, r % q, n, U, R);
    if (p >= q) return euclid(p % q, q, r, n, U, pow(U, p / q) * R);
    long long m = (1ll * p * n + r) / q;
    if (!m) return pow(R, n);
    return pow(R, (q - r - 1) / p) * U * euclid(q, p, (q - r - 1) % p, m - 1, R, U) * pow(R, n - (q * m - r - 1) / p);
}
int T;
int n, a, b, c;
int main() {
    scanf("%d", &T);
    Node U, R;
    U.y = 1, R.x = 1, R.sumx = 1;
    while (T--) {
        scanf("%d%d%d%d", &n, &a, &b, &c);
        auto ans = euclid(a, c, b, n, U, R);
        ans.sumy = (ans.sumy + (b / c)) % P;
        ans.sumy2 = (ans.sumy2 + 1ll * (b / c) * (b / c)) % P;
        printf("%lld %lld %lld\n", ans.sumy, ans.sumy2, ans.sumxy);
    }
    return 0;
}

LOJ6440 万能欧几里得算法

我们要维护 $\sum A^x B^y$，考虑维护出 $A^x, B^y, \sum A^x B^y$ 即可解决。

注意矩阵乘法没有交换律，所以合并的顺序必须是 $\sum A_l^x B_l^y + A_l^x (\sum A_r^xB_r^y) B_l^y$。

#include <bits/stdc++.h>
using namespace std;
const int P = 998244353;
const int MAXN = 22;
int n;
struct Matrix {
    int a[MAXN][MAXN];
    int* operator[](int b) { return a[b]; }
    const int* operator[](const int b) const { return a[b]; }
    Matrix() { memset(a, 0, sizeof a); }
    Matrix(int n) { memset(a, 0, sizeof a); for (int i = 1; i <= n; i++) a[i][i] = 1; }
    Matrix operator*(const Matrix &b) const {
        Matrix c;
        for (int k = 1; k <= n; k++) {
            for (int i = 1; i <= n; i++) {
                for (int j = 1; j <= n; j++) {
                    c[i][j] = (c[i][j] + 1ll * a[i][k] * b[k][j]) % P;
                }
            }
        }
        return c;
    }
    Matrix operator+(const Matrix &b) const {
        Matrix c;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                c[i][j] = (a[i][j] + b[i][j]) % P;
            }
        }
        return c;
    }
};
struct Node {
    Matrix sum, x, y;
    Node() : sum(), x(n), y(n) {}
    Node operator*(Node b) {
        Node a = *this, c;
        c.sum = a.sum + a.x * b.sum * a.y;
        c.x = a.x * b.x;
        c.y = a.y * b.y;
        return c;
    }
};
Node pow(Node a, int b) {
    Node ans;
    while (b) {
        if (b & 1) ans = ans * a;
        a = a * a;
        b >>= 1;
    }
    return ans;
}
Node euclid(long long p, long long q, long long r, long long n, Node U, Node R) {
    if (!n) return Node();
    if (r >= q) return pow(U, r / q) * euclid(p, q, r % q, n, U, R);
    if (p >= q) return euclid(p % q, q, r, n, U, pow(U, p / q) * R);
    long long m = ((__int128_t) p * n + r) / q;
    if (!m) return pow(R, n);
    return pow(R, (q - r - 1) / p) * U * euclid(q, p, (q - r - 1) % p, m - 1, R, U)
         * pow(R, n - ((__int128_t) q * m - r - 1) / p);
}
long long p, q, r, l;
int main() {
    scanf("%lld%lld%lld%lld%d", &p, &q, &r, &l, &n);
    Node U, R;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            scanf("%d", &R.x[i][j]);
            R.sum[i][j] = R.x[i][j];
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            scanf("%d", &U.y[i][j]);
        }
    }
    auto ans = euclid(p, q, r, l, U, R);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            printf("%d ", ans.sum[i][j]);
        }
        printf("\n");
    }
    return 0;
}

CF868G El Toll Caves

好难啊。好难啊。好难啊。

首先容易猜到最优策略是每次选相邻的 $k$ 个，然后绕着一个环依次选。证明咕了。

那么我们设 $f_i$ 为从 $i$ 开始，找到的期望次数。那么我们有 $f_{i + k} = f_{i} + 1\ (i+k < n)$，$f_{i + k - n} = \frac{1}{2}(f_{i} + 1) + \frac{1}{2} = \frac{1}{2} f_{i} + 1$。容易想到系数递推，考虑用 $f_0$ 表示所有数，那么就是 $f_i = k_i f_0 + b_i$。

首先容易发现，如果 $\gcd(n, k) \ne 1$，让两者同时除以 $\gcd(n, k)$ 答案是不变的，那么假定 $\gcd(n, k) = 1$。这时候，容易发现 $ik \bmod n$ 是能不重不漏经过所有 $i$ 的，也就是说，一直将这些函数复合下去，这条链一定会不重不漏经过所有数，最后回到 $0$。那么我们实际上只需要沿着这条链走下去，直到回到 $f_0$，途中维护 $k_i f_0 + b_i$ 的和与 $f_0, k_0$ 的值即可。后者我们可以解出 $f_0$ 的值，前者我们可以计算答案。答案等于 $\frac{1}{n} \sum f_i$。

那么考虑如何计算这个东西。容易发现，这个函数在每次 $ \ge n$ 的时候会发生改变。那么我们构造一条直线 $y=\frac{kx}{n}$。容易发现，这个函数每次经过横向网格时，一定 $\ge n$。那么，相当于每次 $U$ 时，会先将 $f_i$ 乘上 $\frac{1}{2}$，在 $R$ 的时候，会将 $f_i$ 加 $1$，然后累计到和中。那么我们可以设一个二元组 $(f(x), g(x))$ 为两个一次函数，分别表示此时的 $k_i f_0 + b_i$ 与 $\sum k_i f_0 + b_i$。合并时，有 $(A(x), B(x)) * (C(x), D(x)) = (C(A(x)), B(x) + D(A(x)))$，于是直接合并即可。

#include <bits/stdc++.h>
using namespace std;
const int P = 1000000007;
int T, n, k;
struct Node {
    int k1, b1, k2, b2;
    Node() : k1(1), b1(0), k2(0), b2(0) {}
    Node operator*(Node b) {
        Node a = *this, c;
        c.k1 = 1ll * a.k1 * b.k1 % P;
        c.b1 = (1ll * b.k1 * a.b1 + b.b1) % P;
        c.k2 = (a.k2 + 1ll * a.k1 * b.k2) % P;
        c.b2 = (a.b2 + 1ll * a.b1 * b.k2 + b.b2) % P;
        return c;
    }
};
Node pow(Node a, int b) {
    Node ans;
    while (b) {
        if (b & 1) ans = ans * a;
        a = a * a;
        b >>= 1;
    }
    return ans;
}
Node euclid(long long p, long long q, long long r, long long n, Node U, Node R) {
    if (!n) return Node();
    if (r >= q) return pow(U, r / q) * euclid(p, q, r % q, n, U, R);
    if (p >= q) return euclid(p % q, q, r, n, U, pow(U, p / q) * R);
    long long m = ((__int128_t) p * n + r) / q;
    if (!m) return pow(R, n);
    return pow(R, (q - r - 1) / p) * U * euclid(q, p, (q - r - 1) % p, m - 1, R, U)
         * pow(R, n - ((__int128_t) q * m - r - 1) / p);
}
int qpow(int a, int b) {
    int ans = 1;
    while (b) {
        if (b & 1) ans = 1ll * ans * a % P;
        a = 1ll * a * a % P;
        b >>= 1;
    }
    return ans;
}
int main() {
    scanf("%d", &T);
    Node U, R;
    U.k1 = (P + 1) / 2;
    R.k1 = 1, R.b1 = 1, R.k2 = 1, R.b2 = 1;
    while (T--) {
        scanf("%d%d", &n, &k);
        int g = __gcd(n, k); n /= g, k /= g;
        auto ans = euclid(k, n, 0, n, U, R);
        int x = 1ll * ans.b1 * qpow(1 - ans.k1 + P, P - 2) % P;
        printf("%lld\n", (1ll * ans.k2 * x + ans.b2) % P * qpow(n, P - 2) % P);
    }
    return 0;
}

posted @ 2023-06-19 21:05 APJifengc 阅读(1209) 评论(3) 编辑收藏举报

刷新页面返回顶部

apjifengc's blog

【学习笔记】万能欧几里得算法

P5170 【模板】类欧几里得算法

LOJ6440 万能欧几里得算法

CF868G El Toll Caves