「解题报告」P9195 [JOI Open 2016] JOIRIS

发现上午高强度想题之后下午就啥都不想干了。

神秘构造题，我属实是啥也不会了。

先把下标改成从 \(0\) 开始。

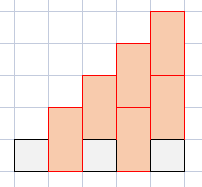
首先看到格子上的连续 \(k\) 的骨牌显然能想到将格子 \(k\) 染色。而由于有删除一行的操作，按照普通的染色方法好像并不好看，所以我们按列染色。这样我们统计每个颜色上的格子的数量\(\bmod k\)，记 \(b_i = (\sum_{i \equiv j \pmod k} a_j) \bmod k\)。那么我们发现，对于横着放的一个骨牌，会使得每个 \(b_i\) 同时加 \(1\)；对于竖着放的一个骨牌，\(b_i\) 不变；对于消除一行的操作，虽然 \(b_i\) 变化量不完全相同，但是发现对于 \(\lbrack 0, n \bmod k)\) 与 \(\lbrack n \bmod k, n)\) 这两个区间里的 \(b_i\) 的相对大小不会发生改变。所以我们可以得出一个有解必要条件：\(b_0 = b_1 = \cdots = b_{(n \bmod k) - 1}\) 且 \(b_{(n \bmod k)} = b_{(n \bmod k) + 1} = \cdots = b_{n - 1}\)。

接下来我们构造一种方案来证明这是充分条件。

1. 首先我们通过添加若干竖着的骨牌，使得骨牌数量从左到右单调不降；

   

2. 然后我们通过横着平铺，从下到上依次填满每一行；

   

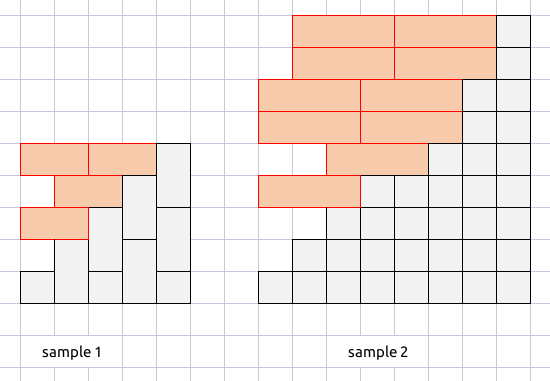
3. 容易发现，此时对于 \(\lbrack k - 1, n)\) 列，高度完全相等。那么，我们通过不断的往 \([0, k - 2]\) 内插入竖着的骨牌，使得 \(\lbrack k - 1, n)\) 全部被删除；

   

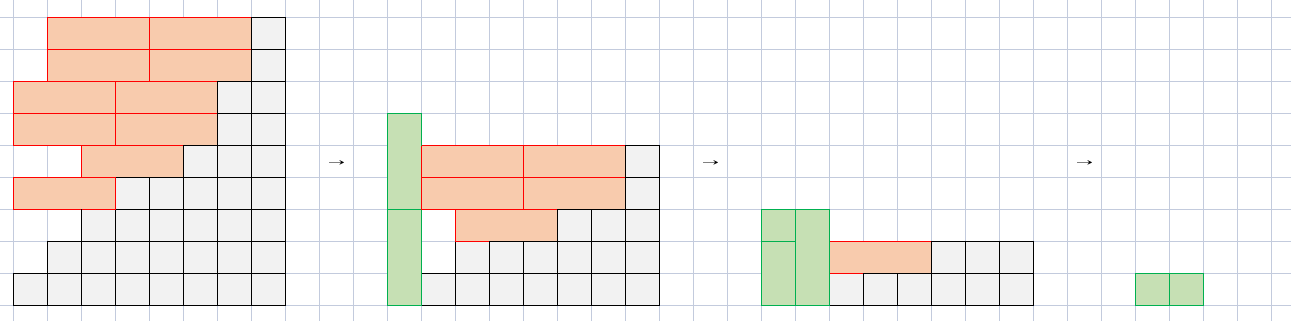
4. 此时我们一定有 \(b_{k - 1} = 0\)。由我们的条件可知，\(b_{(n \bmod k)} = b_{(n \bmod k)} = \cdots = b_{k - 1} = 0\)，那么也就是说对于这些列的 \(a_i\) 一定是 \(k\) 的整数倍，那么我们可以直接插入若干个竖骨牌将这些骨牌删除；

   

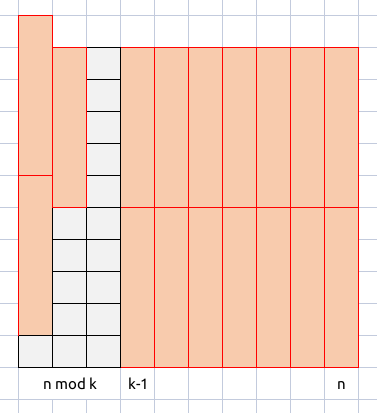
5. 此时一定仅有 \(\lbrack 0, n \bmod k)\) 内有格子了。而由于 \(b_0 = b_1 = \cdots = b_{(n \bmod k) - 1}\)，那么我们可以先将左边补齐，然后在右面横着铺满，即可全部消除。

   

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 55;
int n, k;
int a[MAXN];
int b[MAXN];
vector<pair<int, int>> ans;
void op(int x, int y) {
    ans.push_back({ x, y });
    if (x == 1) {
        a[y] += k;
    } else {
        for (int i = 0; i < k; i++) {
            a[y + i]++;
        }
    }
    int mn = INT_MAX;
    for (int i = 0; i < n; i++) {
        mn = min(mn, a[i]);
    }
    for (int i = 0; i < n; i++) {
        a[i] -= mn;
    }
}
int main() {
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
        b[i % k] = (b[i % k] + a[i]) % k;
    }
    if (k == 1) {
        int mx = 0;
        for (int i = 0; i < n; i++) {
            mx = max(mx, a[i]);
        }
        for (int i = 0; i < n; i++) {
            for (int j = a[i]; j < mx; j++) {
                ans.push_back({ 1, i });
            }
        }
        printf("%lu\n", ans.size());
        for (auto p : ans) {
            printf("%d %d\n", p.first, p.second + 1);
        }
        return 0;
    }
    for (int i = 0; i < k - 1; i++) if (i != (n % k) - 1) {
        if (b[i] != b[i + 1]) {
            printf("-1\n");
            return 0;
        }
    }
    for (int i = 1; i < n; i++) {
        while (a[i] < a[i - 1]) {
            op(1, i);
        }
    }
    for (int i = 1; i < n - 1; i++) {
        int delta = a[i + 1] - a[i];
        for (int j = i - k + 1; j >= 0; j -= k) {
            for (int t = 0; t < delta; t++) {
                op(2, j);
            }
        }
    }
    for (int l = 1; l <= k - 1; l++) {
        for (int i = 0; i < l; i++) {
            int delta = a[n - 1] - a[i];
            while (delta > 0) {
                delta -= k;
                op(1, i);
            }
        }
    }
    int mx = 0;
    for (int i = n % k; i < k; i++) {
        mx = max(mx, a[i]);
    }
    for (int i = 0; i < n; i++) {
        int delta = mx - a[i];
        while (delta > 0) {
            delta -= k;
            op(1, i);
        }
    }
    mx = 0;
    for (int i = 0; i < n % k; i++) {
        mx = max(mx, a[i]);
    }
    for (int i = 0; i < n % k; i++) {
        while (a[i] < mx) op(1, i);
    }
    for (int i = n % k; i < n; i += k) {
        for (int j = 0; j < mx; j++) {
            op(2, i);
        }
    }
    for (int i = 0; i < n; i++) {
        assert(a[i] == 0);
    }
    printf("%lu\n", ans.size());
    for (auto p : ans) {
        printf("%d %d\n", p.first, p.second + 1);
    }
    return 0;
}