「解题报告」UOJ670 [UNR #5] 获奖名单

有趣构造题，和今年省选 D2T2 类似的思路？

首先看到字符串长度为 1 或 2，可以想到建图来转换题目。但是建出图后题目的要求还是不好抽象。

我们可以将回文串的两半拆开（先假设答案恰好划分成了两半），然后对齐在一起。此时我们就发现，只有两种情况，一种是有两个相同的直接拼接在一起，一种是先有一个长为 1 的，然后长为 2 的交替，再为长为 1 的结尾。

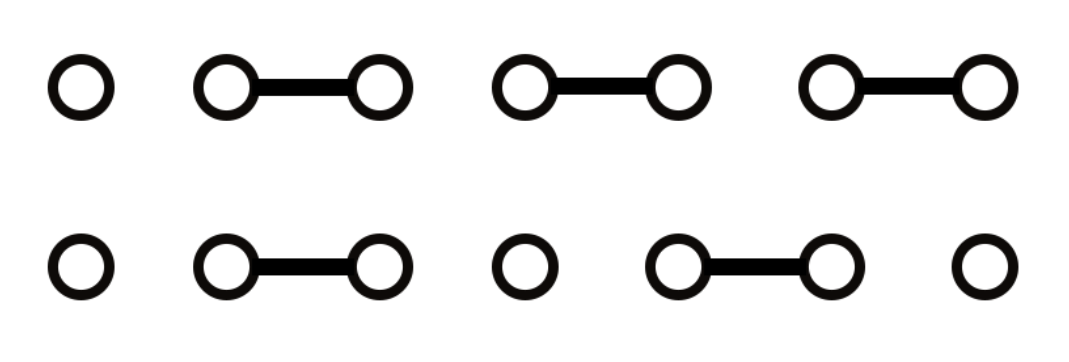
我们发现，对于后者的情况，可以看作是从两个长为 1 的作为起点和终点的一条路径。

我们考虑建立一个源点 0，然后将所有长度为 1 的点连向源点 0。这时候，我们发现，一条路径就变成了一条欧拉回路。那么，我们只需要从源点跑一遍欧拉回路，即可相应的构造出后者交替的情况。前者相同的情况是好构造的，直接放左右两端即可。

此时考虑更一般的情况。首先，对于长度为偶数的情况，有可能中间有一个长度为 2 的串，不能拆开。而由于其它的串都是成对出现的，只有这个串会出现奇数次，于是找出这个串然后放到最中间即可。

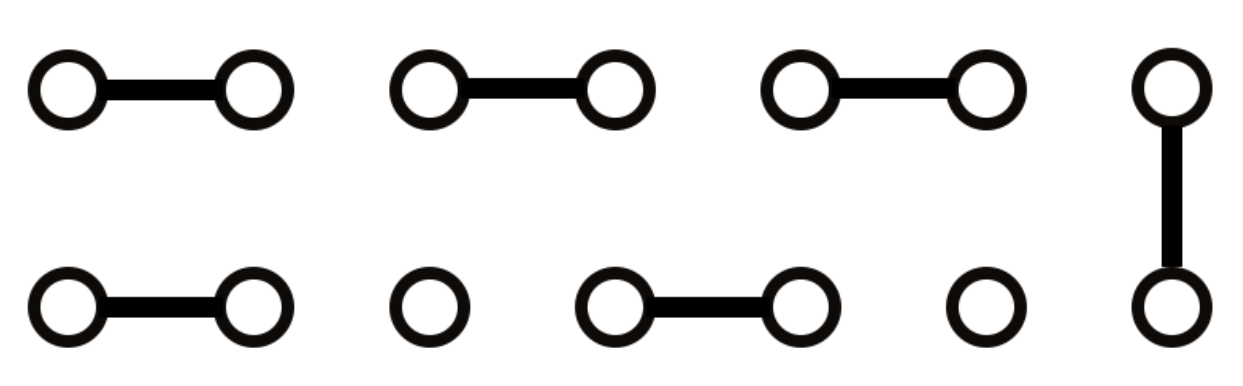
对于长度为奇数的情况，最后会多出来一块，那么此时就不是欧拉回路了，而是欧拉路径。而此时发现，恰好只有 0 点和最后多出的一个点的出现次数为奇数，所以仍然从 0 开始跑一遍欧拉路径即可。

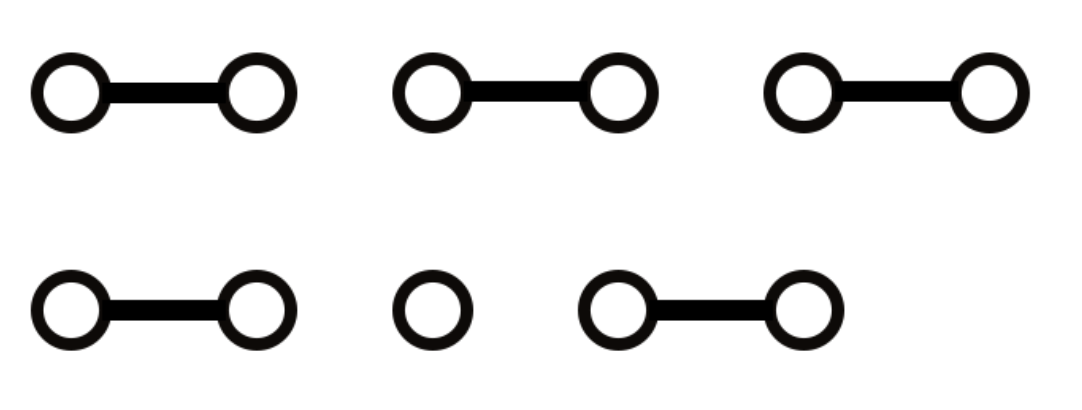
and 这是我不知道第几次忘了怎么求欧拉路径了。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 500005;
int n, m;
int c[MAXN], u[MAXN], v[MAXN];
map<pair<int, int>, vector<pair<int, int>>> mp;
struct Graph {
    int fst[MAXN], nxt[MAXN << 1], to[MAXN << 1], id[MAXN << 1], tot;
    void add(int u, int v, int i) {
        to[++tot] = v, nxt[tot] = fst[u], fst[u] = tot, id[tot] = i;
        to[++tot] = u, nxt[tot] = fst[v], fst[v] = tot, id[tot] = i;
    }
    bool vis[MAXN << 1];
    stack<pair<int, int>> s;
    void dfs(int u) {
        for (int &i = fst[u], v = to[i]; i; i = nxt[i], v = to[i]) if (!vis[id[i]]) {
            vis[id[i]] = 1;
            dfs(v);
            s.push({u, v});
        }
    }
} g;
int ans[MAXN][2];
int main() {
    // freopen("ex_namelist5.in", "r", stdin);
    // freopen("ex_namelist5.out", "w", stdout);
    scanf("%d%d", &n, &m);
    int len = 0;
    for (int i = 1; i <= n; i++) {
        scanf("%d%d", &c[i], &u[i]);
        len += c[i];
        if (c[i] == 2) {
            scanf("%d", &v[i]);
            mp[{min(u[i], v[i]), max(u[i], v[i])}].push_back({i, u[i] > v[i]});
            g.add(u[i], v[i], i);
        } else {
            g.add(0, u[i], i);
            mp[{0, u[i]}].push_back({i, 0});
        }
    }
    g.dfs(0);
    vector<pair<int, int>> a, b, c, d;
    int side = 0;
    while (!g.s.empty()) {
        int u, v; tie(u, v) = g.s.top(); g.s.pop();
        pair<int, int> i = mp[{min(u, v), max(u, v)}].back();
        mp[{min(u, v), max(u, v)}].pop_back();
        i.second ^= u > v;
        if (u == 0) side = 0;
        if (side == 0) a.push_back(i);
        else b.push_back(i);
        side ^= 1;
    }
    pair<int, int> mid;
    for (auto &p : mp) {
        if (p.second.size() & 1) {
            mid = p.second.back();
            p.second.pop_back();
        }
        while (p.second.size()) {
            auto x = p.second.back(); p.second.pop_back();
            auto y = p.second.back(); p.second.pop_back();
            c.push_back(x);
            d.push_back(y);
        }
    }
    reverse(b.begin(), b.end()), reverse(d.begin(), d.end());
    int k = 0;
    for (auto p : c)
        k++, ans[k][0] = p.first, ans[k][1] = p.second;
    for (auto p : a)
        k++, ans[k][0] = p.first, ans[k][1] = p.second;
    if (mid.first) k++, ans[k][0] = mid.first, ans[k][1] = mid.second;
    for (auto p : b)
        k++, ans[k][0] = p.first, ans[k][1] = p.second ^ 1;
    for (auto p : d)
        k++, ans[k][0] = p.first, ans[k][1] = p.second ^ 1;
    assert(k == n);
    for (int i = 1; i <= n; i++) {
        printf("%d ", ans[i][0]);
    }
    printf("\n");
    for (int i = 1; i <= n; i++) {
        printf("%d ", ans[i][1]);
    }
    printf("\n");
    return 0;
}