「解题报告」ARC128F Game against Robot

好厉害的题。震撼到了。

大部分参考 Atcoder 计数乱做 - 苹果蓝17。

我的观察能力还是太差，一点条件都观察不出来，连 \(p\) 固定怎么做都不会。

下面令 \(n \gets \frac{n}{2}\)。

首先考虑对于一个固定的 \(p\) 要怎么做。考虑对方可以选的集合的充要条件，发现只需要选的第 \(i\) 个数在前 \(2i\) 个数内即可。那么相对应的，把整个过程反过来，自己可以选的第 \(i\) 个数就在后 \(2i\) 个数内。那么我们就可以从后往前，每次往优先队列里加入两个数，每次取最大值，就是答案。

这个做法告诉我们，最后答案实际上只跟相对大小关系有关，所以我们考虑统计每个数在多少种方案中被选择。设第 \(i\) 大的数被统计的方案数为 \(f_i\)，那么答案就是 \(\sum_{i=1}^{2n} f_i a_i\)。

第 \(i\) 大还是很难统计，考虑降低值域，改为求前 \(m\) 大的数被统计的方案数 \(g_m\)。这样，我们可以将前 \(m\) 大的数设为 \(1\)，其余的数设为 \(0\)，这样我们只需要考虑每种 \(01\) 序列中被选取的 \(1\) 的数量。注意我们这时候不考虑 \(0,1\) 之间的顺序，最后我们再乘上一个 \(m!(2n-m)!\)。

考虑这个 \(01\) 序列长什么样子。我们按照每两位分组，设第 \(i\) 组有 \(c_i\) 个 \(1\)，那么有 \(\sum_{i=1}^n c_i = m\)。考虑优先队列的过程，我们设优先队列中有 \(x\) 个 \(1\)，那么根据上面的贪心策略，可以得到每一次 \(x \gets \max(0, x + c_i - 1)\)。

我们设 \(d_i = c_i - 1\)，然后把这个过程放到网格图上，看作每次向右、右上或右下走一个，如果低于了 \(x\) 轴就强行扳回 \(x\) 轴。

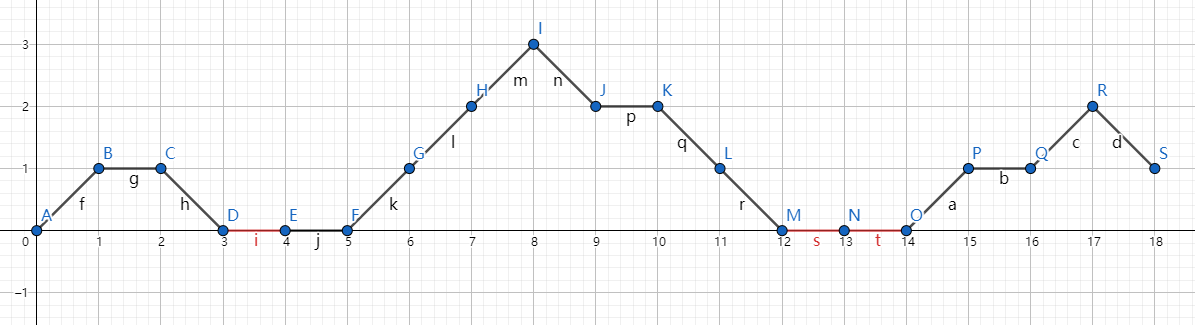
红线表示扳回 \(x\) 轴的位置，也意味着选 \(0\) 的位置。这个东西看起来很丑，我们考虑把 \(\max\) 去掉，就会变成这样：

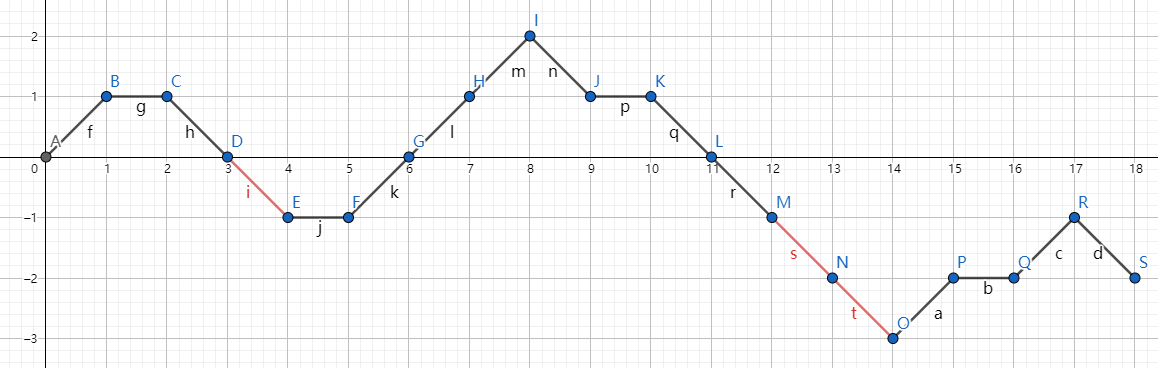
可以发现，每个红线都使得整体最小值减小了 \(1\)，那么红线的数量就等于全局最小值的绝对值。

那么假如全局最小值为 \(k\)，那么红线的数量为 \(-k\)，那么选取的 \(1\) 的数量就是 \(n + k\)。

那么我们只需要统计有多少种 \(01\) 序列使得最小值为 \(k\)。这种东西可以类似于卡特兰数的推导方式来计算。

我们先给出一个引理：

从 \((0, 0)\) 开始走，向右走（\(c_i=1\)）的方案数为 \(2\)，向右上或右下（\(c_i=0 / 2\)）的方案数为 \(1\)，那么从 \((0, 0)\) 走到 \((n, m)\) 的方案数为 \(\binom{2n}{n + m}\)。

证明：方案数实际上等于 \([x^m] (x^{-1} + 2 + x)^n\)。

\[\begin{aligned} &[x^m] (x^{-1} + 2 + x)^n\\ =&[x^m] x^{-n} (1 + 2x + x^2)^n\\ =&[x^{n+m}](x+1)^{2n}\\ =&\binom{2n}{n+m} \end{aligned} \]

那么我们就可以类似于卡特兰数的方式求解这个问题了。

我们相当于要从 \((0, 0)\) 走到 \((n, m - n)\) 的位置，求经过最低点为 \(k\) 的方案数。那么用卡特兰数的折线的方案可以得出最低点大于等于 \(k\) 的方案数，即：

\[\binom{2n}{n + m - n} - \binom{2n}{n + 2(k - 1) - (m - n)}=\binom{2n}{m} - \binom{2n}{m - 2k + 2} \]

那么恰好 \(k\) 的方案数就是：

\[\binom{2n}{m-2k} - \binom{2n}{m - 2k + 2} \]

那么统计答案：设 \(p = \max(0, n - m)\)，那么最小值的取值为 \([-n, -p]\)，那么有：

\[\begin{aligned} \frac{g_m}{m!(2n-m)!}=& \sum_{k=-n}^{-p} (n+k) \left(\binom{2n}{m - 2k} - \binom{2n}{m - 2k + 2}\right)\\ =& \sum_{k=p}^{n} (n-k) \left(\binom{2n}{m + 2k} - \binom{2n}{m + 2(k + 1)}\right)\\ =& n\sum_{k=p}^{n} \left(\binom{2n}{m + 2k} - \binom{2n}{m + 2(k + 1)}\right) - \sum_{k=p}^{n} k\binom{2n}{m + 2k} + \sum_{k=p}^{n} k\binom{2n}{m + 2(k + 1)}\\ =& n \binom{2n}{m + 2p} - \sum_{k=p} k\binom{2n}{m + 2k} + \sum_{k=p + 1} (k - 1)\binom{2n}{m + 2k}\\ =& n \binom{2n}{m + 2p} - p\binom{2n}{m + 2p} - \sum_{k=p + 1}^n \binom{2n}{m + 2k}\\ \end{aligned} \]

后面那个式子可以前缀和一下，然后就 \(O(1)\) 了。

然后最后的答案就是 \(\sum_{i=1}^{2n} a_i (g_i - g_{i - 1})\)。

你不觉得这很酷吗？我觉得这太酷了。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2000005, P = 998244353;
int n, a[MAXN];
int fac[MAXN], inv[MAXN];
int C(int n, int m) {
    if (n < 0 || m < 0 || n < m) return 0;
    return 1ll * fac[n] * inv[m] % P * inv[n - m] % P;
}
int qpow(int a, int b) {
    int ans = 1;
    while (b) {
        if (b & 1) ans = 1ll * ans * a % P;
        a = 1ll * a * a % P;
        b >>= 1;
    }
    return ans;
}
int pre[MAXN];
int f[MAXN];
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }
    sort(a + 1, a + 1 + n, greater<>());
    fac[0] = 1;
    for (int i = 1; i <= n; i++) {
        fac[i] = 1ll * fac[i - 1] * i % P;
    }
    inv[n] = qpow(fac[n], P - 2);
    for (int i = n; i >= 1; i--) {
        inv[i - 1] = 1ll * inv[i] * i % P;
    }
    assert(inv[0] == 1);
    n /= 2;
    pre[0] = C(2 * n, 0), pre[1] = C(2 * n, 1);
    for (int i = 2; i <= 4 * n; i++)
        pre[i] = (pre[i - 2] + C(2 * n, i)) % P;
    for (int m = 0; m <= 2 * n; m++) {
        int lim = max(n - m, 0);
        f[m] = (1ll * n * C(2 * n, m + 2 * lim) % P 
            - 1ll * lim * C(2 * n, m + 2 * lim) % P 
            - (pre[m + 2 * n] - pre[m + 2 * lim]) + 2 * P) % P * fac[m] % P * fac[2 * n - m] % P;
    }
    int ans = 0;
    for (int i = 1; i <= 2 * n; i++) {
        ans = (ans + 1ll * a[i] * (f[i] - f[i - 1] + P)) % P;
    }
    printf("%d\n", ans);
    return 0;
}