「解题报告」CF1444D Rectangular Polyline

这类型的题我们可以先找一些显然的必要条件，然后再去构造，很有可能就发现它是充分条件。

考虑有什么必要条件：首先 \(n=m\)，要不然无法横纵首尾相连。

其次所有横必定能划分成两个和相等的集合，纵一样。

那么我们首先跑个背包将横纵划分成两个集合，这样我们相当于有了若干向量，我们要将它们连成一个多边形。

考虑先将一个横向量和一个纵向量合成为一个斜向量。那么我们得到了 \(n\) 个斜向量。按照极角排序首尾相连，我们便能得到一个凸多边形。

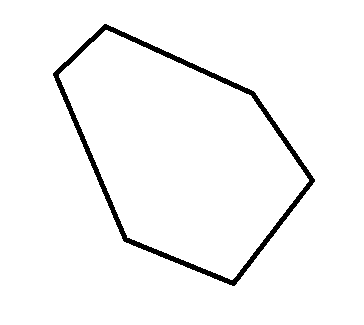
但是问题是，虽然这个凸多边形两两不交，但是形成的多边形可能有交。

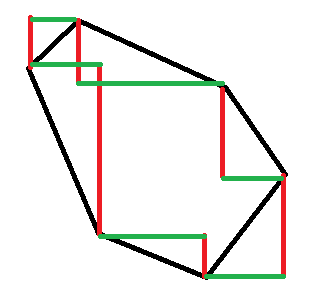
那怎么办呢？我们发现，能够发生相交的向量只有二三象限（或一四象限）。假如我们让这其中一个象限没有向量，就一定不会有交了。

事实上，当我们将横向量和纵向量相加的时候，只需要先对横纵向量进行排序，就只会得到三个象限的向量。

这个很容易发现，不举例子了。

那么我们只需要先排序，结合起来，再按照极角排序，输出答案即可。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1005;
int T;
int n, m;
int a[MAXN], b[MAXN];
bitset<2 * MAXN * MAXN> f[MAXN];
pair<int, int> c[MAXN];
bool operator<(pair<int, int> a, pair<int, int> b) {
    return atan2(a.second, a.first) < atan2(b.second, b.first);
}
int main() {
    scanf("%d", &T);
    while (T--) {
        scanf("%d", &n);
        for (int i = 1; i <= n; i++) {
            scanf("%d", &a[i]);
        }
        scanf("%d", &m);
        for (int i = 1; i <= m; i++) {
            scanf("%d", &b[i]);
        }
        if (n != m) {
            printf("No\n");
            continue;
        }
        {
            for (int i = 0; i <= n; i++) {
                f[i].reset();
            }
            f[0][MAXN * MAXN] = 1;
            for (int i = 1; i <= n; i++)
                f[i] = (f[i - 1] << a[i]) | (f[i - 1] >> a[i]);
            if (!f[n][MAXN * MAXN]) {
                printf("No\n");
                continue;
            }
            int s = MAXN * MAXN;
            for (int i = n; i >= 1; i--) {
                if (f[i - 1][s + a[i]]) {
                    s += a[i];
                    a[i] *= -1;
                } else {
                    s -= a[i];
                }
            }
        }
        {
            for (int i = 0; i <= n; i++) {
                f[i].reset();
            }
            f[0][MAXN * MAXN] = 1;
            for (int i = 1; i <= n; i++)
                f[i] = (f[i - 1] << b[i]) | (f[i - 1] >> b[i]);
            if (!f[n][MAXN * MAXN]) {
                printf("No\n");
                continue;
            }
            int s = MAXN * MAXN;
            for (int i = n; i >= 1; i--) {
                if (f[i - 1][s + b[i]]) {
                    s += b[i];
                    b[i] *= -1;
                } else {
                    s -= b[i];
                }
            }
        }
        sort(a + 1, a + 1 + n);
        sort(b + 1, b + 1 + n, greater<>());
        printf("Yes\n");
        for (int i = 1; i <= n; i++) {
            c[i] = { a[i], b[i] };
        }
        sort(c + 1, c + 1 + n);
        int x = 0, y = 0;
        for (int i = 1; i <= n; i++) {
            printf("%d %d\n", x, y);
            y += c[i].second;
            printf("%d %d\n", x, y);
            x += c[i].first;
        }
    }
    return 0;
}