3.9 听课记录
远程蹭了个课，lxl 讲的青蛙很不错。
先都口胡一下，回头再补代码，没时间写。
倍增值域分块
倍增值域分块的思想，就是将值域分块为 \([2^k, 2^{k+1})\) 的形式，这种问题很多有类似于若 \(c\ge w, c \gets c - w\) 的操作，具体看例题。
CF1515I Phoenix and Diamonds
有 \(n\) 种二元组 \((w_i, v_i)\) 和一个由这些二元组序列组成的序列，按照 \(v_i\) 为第一关键字从大到小，\(w_i\) 为第二关键字从小到大排序，初始时有第 \(i\) 种二元组 \(a_i\) 个。
接下来你要进行 \(m\) 次操作，操作有三种：
- 加入 \(k\) 个 \((w_d, v_d)\) 二元组。
- 删除 \(k\) 个 \((w_d, v_d)\) 二元组。
- 给定一个 \(c\)，从左往右依次枚举二元组，若 \(c \ge w_i\)，则令 \(c \gets c - w_i, ans \gets ans + v_i\)，求最后的 \(ans\) 等于多少。
\(n \le 2\times 10^5, m \le 10^5, c \le 10^{18}\)
我们将值域按照 \([2^k, 2^{k + 1})\) 进行分块。然后我们考虑当前的 \(c\) 所在的某一块。
考虑我们枚举到的所有可能的 \(w_i\)，有三种情况，\(w_i < 2^k, w_i \in [2^k, 2^{k - 1}), w_i \ge 2^{k + 1}\)。
第三种情况肯定是不会被统计到的，考虑前两种情况。
如果出现了 \(w_i \in [2^k, 2^{k - 1})\)，那么我们发现 \(c - w < 2^k\)，那么此时的 \(c\) 一定就会掉到更小的那一块中。那么，当 \(c\) 一直在原来这一块中时，经过的可能全部都是 \(w_i < 2^k\)，也可能经过了若干 \(w_i < 2^k\)，最后经过了一个 \(w_i \in [2^k, 2^{k - 1})\)。
那么我们可以对每一块开一颗线段树来维护这个东西。对于前者，我们在线段树上维护所有 \(w_i < 2^k\) 的值，然后每次可以在线段树上二分找到最小的使得 \(c < 2^k\) 的 \(w_i\) 的值；对于后者，我们在线段树上维护所有 \(w_i \in [2^k, 2^{k + 1})\) 的值，同样可以二分找到那个点。
这样我们只需要比较两种情况哪个先掉下 \(c\) 即可。而注意到只有 \(\log V\) 组，这就意味着只会掉下 \(\log V\) 次，于是直接暴力一直往下跳即可。这样单次询问复杂度就是 \(O(\log V \log n)\)。
修改也是容易的，发现上述两棵线段树的值都是容易维护的，直接维护即可。
LOJ3527 「IOI2021」地牢游戏
发现这题和上一题非常类似，同样可以用类似的方式进行分块。
对于 \(w_i < 2^k\) 的情况，我们会一直恰烂分，同样对于 \(w_i \ge 2^{k + 1}\)，我们会一直战败。当碰到一个 \(w_i \in [2^k, 2^{k + 1})\) 的敌人时，我们如果能够击败，那么此时的 \(c\) 一定会升高一个块，否则同样会战败。
但是这道题是类似于一个图的东西，并不好维护。我们类似于上一题的做法，考虑全部都是 \(w_i < 2^k\) 和战败的情况，那么我们可以确定每次走的道，这样就可以倍增处理这个东西了。存在 \(w_i \in [2^k, 2^{k + 1})\) 的做法一样，也可以用倍增来维护。不带修，于是就很好维护。
P4587 [FJOI2016]神秘数
一个可重复数字集合 \(S\) 的神秘数定义为最小的不能被 \(S\) 的子集的和表示的正整数。例如 \(S=\{1,1,1,4,13\}\)，有：\(1 = 1\)，\(2 = 1+1\)，\(3 = 1+1+1\)，\(4 = 4\)，\(5 = 4+1\)，\(6 = 4+1+1\)，\(7 = 4+1+1+1\)。
\(8\) 无法表示为集合 \(S\) 的子集的和，故集合 \(S\) 的神秘数为 \(8\)。
现给定长度为 \(n\) 的正整数序列 \(a\)，\(m\) 次询问，每次询问包含两个参数 \(l,r\)，你需要求出由 \(a_l,a_{l+1},\cdots,a_r\) 所组成的可重集合的神秘数。
对于 \(100\%\) 的数据点，\(1\le n,m\le {10}^5\)，\(\sum a\le {10}^9\)。
题目实际上是求所有子集和的 \(\rm mex\)。
我们维护一个所有数都能被表示出来的前缀，然后每次考虑这个前缀中新增加的数。如果 \([1, r]\) 中的所有数都能被表示，那么在这些新增加的数 \(x_1, x_2, \cdots\) 的组合下，就可以表示出 \([1, r + x_1 + x_2 + \cdots]\) 中的所有数。
我们发现，由于 \(\sum x\) 一定大于上一个前缀的长度，那么每进行这样的操作两次，一定能够使得长度翻倍。那么我们只需要一个动态二位数点，上主席树即可。复杂度 \(O(n \log^2 n)\)。
如果带修呢？
2019 ICPC 徐州 H Yuuki and a problem
同上述问题，需要支持单点修改。
如果直接套上述做法需要一个树状数组套可持久化线段树，复杂度 \(O(n \log^3 n)\)，不能接受。
上述问题的瓶颈其实在于我们需要支持一个动态的二位数点，其中两维都是动态的。
我们能不能通过对值域分块使得一种一维变成静态的？
考虑利用 \([2^k, 2^{k + 1})\) 的值域分块。我们发现，假如当前能表示的区间能够覆盖 \([2^k, 2^{k + 1})\) 中的最小的一个值，那么我们就能覆盖整个 \([2^k, 2^{k + 1})\) 区间，也就一定能覆盖到下一个块。那么这样我们每次只需要知道 \([2^k, 2^{k + 1})\) 中的最小值与和，只用线段树就可以维护了。这样复杂度就降为了 \(O(n \log^2 n)\)。
这样我们可以发现，这个 trick 的实质是将 \(O(V)\) 的值域压缩为了 \(O(\log V)\)，这样就可以暴力对值域进行维护。
P7447 [Ynoi2007] rgxsxrs
给定一个长为 \(n\) 的序列 \(a\)，需要实现 \(m\) 次操作：
1 l r x：表示将区间 \([l,r]\) 中所有 \(>x\) 的元素减去 \(x\)。
2 l r：表示询问区间 \([l,r]\) 的和，最小值，最大值。对于 \(100\%\) 的数据，\(1\le n,m\leq 5\times 10^5\)，\(1\leq a_i,x\leq 10^9\)。
强制在线，空间限制 64 MB。
考虑到每个数只增不减，所以可以类似于势能的方法去维护。但是值域太大，仍然无法接受。
我们考虑对值域分块，对整个值域中的数进行维护。那么考虑 \(x\) 所在的区间 \([2^k, 2^{k + 1})\)，对于大于这个块的数，可以直接全局减，如果小于 \(0\) 则将这个数放到下一个块中。而在这个块中的数，减去后一定会到更小的一个块，所以可以直接枚举所有的 \(>x\) 的数进行修改。每个数最多被下放 \(\log V\) 个块，复杂度就为 \(O(n \log n \log V)\)。
减半警报器
一类神奇的问题，可以以 \(O(\log V)\) 的代价将多元限制转换成单元限制。
Codeforces GYM 102452 I
有 \(n\) 个地点，每个地点可能会发生若干次事件，事件有一个权值。
有若干次监测活动，每次会在 \(k\) 个地点 \(x_1, x_2, \cdots, x_k\)（\(k\le 3\)）放置监视器，若监视器监视到的地点发生的事件的权值和大于等于 \(c\)，则发生警报。
有 \(m\) 次操作：
- \(1\ k\ x_1\ x_2\ \cdots\ x_k\ c\)：启动一次监视活动。
- \(2\ k\ c\)：在 \(k\) 地点发生了一次权值为 \(c\) 的事件。
在每次 \(2\) 操作后，输出发生警报的监视活动的编号，忽略之前已经发生过的警报。
\(n \le 2\times 10^5, m \le 10^6\)。
假如 \(k=1\)，那么这题是很好做的，直接在每个点挂一个活动，然后每次让这个区间上的所有值减 \(c\)，然后找所有权值小于等于 \(0\) 的即可。
对于 \(k=2\) 来说，两个点是有互相限制的。我们可以弄出一个二维平面，然后对矩形进行操作，但这无非要上 KD-Tree，复杂度肯定不咋好看，\(k=3\) 更炸裂。
考虑将互相限制拆开。我们可以先将每个监视活动的 \(c\) 对半分，分配给两个地点，当成 \(k=1\) 来做。假如说其中一个点小于等于 \(0\) 了，我们可以相应的看看另一个点有没有到 \(0\)，如果没有，就把另一个点的权值拿出来，接着对半分。容易发现，这样每一次活动最多只会触发 \(\log V\) 次警报，这样就能把两两限制拆开了。
\(k=3\) 是一样的，容易发现也是 \(\log V\) 次。对于较小的常数个来说，其得到的都是 \(\log V\) 次。
P7603 [THUPC2021] 鬼街
lxl 瑞平 THUPC。
实际上发现这个题和上一个题一模一样，由某个众所周知的表，可以发现质因子个数最多为 \(6\)，然后直接套上一个题的做法就完了。
Codeforces GYM 104065 B
你可以邀请 \(n\) 个人来参加会议，第 \(i\) 个人会参加会议当且仅当在 \([l_i, r_i]\) 中至少有 \(k_i\) 个人参加会议，问最多有多少人参加会议。
\(n \le 4 \times 10^5\)
首先容易发现肯定是每次邀请能邀请的，类似于一个拓扑排序的过程。直接模拟这个过程即可。
那么我们实际上每次要找的就是已经满足了条件的人。
看起来和上一题是类似的，但是这次每个人的地点并不是常数个，直接套肯定不行。
考虑将一段区间分成两段。我们先假设所有区间都经过某一点 \(p\)，那么我们可以在 \(p\) 点将所有区间全部断开，这样就得到了一堆前缀和一堆后缀。那么我们将限制分给前缀和后缀，按照前缀后缀的长度排序，每次修改的就是一段连续区间了。
不在同一个区间呢？直接考虑分治，所有区间要不然经过中点，要不然完全在左边，要不然完全在右边。
那么这个分治过程其实就是棵线段树，直接类似于线段树单点修改即可。
每个前缀只出现一次，所以每个节点被修改的复杂度仍然是 \(O(n \log V \log n)\)，单点修改的复杂度是 \(O(n \log ^ 2n)\)，所以总复杂度仍然是两个 \(\log\)。
Codeforces GYM 102331 F
给你 \(n\) 个点，点 \(i\) 有点权 \(v_i\)，有 \(m\) 个三元组 \((a_i, b_i, w_i)\)，不断进行以下操作：
- 找出最小的一个 \(i\)，满足 \(a_i, b_i\) 不连通，且 \(a_i, b_i\) 所在的连通块的点权和 \(\ge w_i\)；
- 若存在 \(i\)，则联通 \(a_i, b_i\)；否则，停止操作。
你需要输出最后一共联通了多少，以及联通的顺序。
\(n, m \le 3 \times 10^5\)
完全类似的，我们考虑维护出每个连通块的所有出边（三元组），那么每次合并两个连通块就是让这些出边的权值减去另一个连通块的权值和。同样将权值平分到两个连通块上，拿平衡树或者线段树维护，合并即可。
\(O(n \log n)\) 支配对
很多题我们需要统计区间内每一对数的贡献，而对数是 \(O(n^2)\) 的。但是，存在很多对是无用的，有某一个对包含了这个对，且贡献可以覆盖掉这个对。我们相当于有若干支配的关系，这样的支配关系很可能能缩小至 \(O(n \log n)\) 甚至 \(O(n)\) 级别，可以使用二维数点等方式进行统计。
lxl 将这类问题分为了两类，这里也分一下吧。
第一类支配对
贡献对数为 \(\Omega(n^2)\)，但本质不同的有 \(O(n)\) 种。
常见于树上，两两求 \(\rm lca\) 相关的权值，而 \(\rm lca\) 只有 \(O(n)\) 个，所以可以对每个 \(\rm lca\) 统计支配对。而 \(\rm lca\) 的点对可以通过启发式合并得出。
P7880 [Ynoi2006] rldcot
给定一颗树，每次询问一个区间 \([l, r]\)，求对于所有的 \(l \le u < v \le r\)，本质不同的 \({\rm dep}( {\rm lca}(u, v))\) 有多少。
\(n, m \le 5 \times 10^5\)
先不管深度，先考虑 \(\rm lca\) 本质不同的有多少。
考虑启发式合并，每插入一个点 \(v\)，假如原来已经有 \(u_1 < u_2\) 两个点满足 \(u_1 < u_2 < v\)，那么我们发现，\((u_2, v)\) 一定比 \((u_1, v)\) 更优，那么相当于我们每次只需要找出前驱和后继两个点组成的点对。
可是此时还是会出现算重的情况。但是注意到最后要查询的实际上是一个矩形查询，而每个点能造成影响的点为一个矩形，为了避免算重，我们可以用扫描线求矩形并，这样就能处理出本质不同的数量了。
对于深度来说，我们把深度相同的点一块做类似于矩形并的东西即可。实际上由于矩阵的形式直接维护最大高度即可。
P8528 [Ynoi2003] 铃原露露
给定一棵树，每次询问一个区间 \([l, r]\)，求有多少 \(l \le L \le R \le r\) 满足对于任意 \(L \le u, v \le R\)，都有 \(L \le \mathrm{lca}(u, v) \le R\)。
\(n, m \le 2 \times 10^5\)
全部都满足很抽象，我们可以改成求存在一个不满足，这样求矩阵并就是所有不满足的情况。
什么情况下不满足呢？还是考虑对于每一个点作为 \(\mathrm{lca}\) 的时候的点对。假如此时有某个 \(u < v < \mathrm{lca}(u, v)\)，那么对于所有 \(L \le u,R \in [v, \mathrm{lca}(u, v))\) 的 \([L, R]\) 就都不合法。
同样考虑支配关系，假如有某个 \(u_1 < u_2 < v\)，那么我们发现 \(u_2\) 的不合法情况完全包含了 \(u_1\) 的不合法情况。所以我们只需要考虑最大的 \(u < v\)。反之亦然。所以同样只需要将前驱后继找出来即可。
那么接下来就是一个区间并的问题了，线段树维护最小值和最小值的个数之类的东西就能求出来了。
第二类支配对
贡献对数为 \(\Omega(n^2)\)，本质不同的也有 \(O(n^2)\) 种。
常见于序列上求区间内所有点对的贡献的 \(\min / \max\)。
这种问题一半考虑对于某一个左端点，有 \(O(\log n)\) 个有用的右端点。
CF765F Souvenirs
给定一个序列 \(a_1, a_2, \cdots, a_n\)，每次询问一个区间 \([L, R]\)，求 \(u, v \in [L, R], u \ne v, |a_u - a_v|\) 的最小值。
\(n \le 10^5, m \le 3 \times 10^5\)
老经典题了。
考虑对于某个 \(u\)，有多少有用的 \(v > u\)。首先 \(u + 1\) 肯定有用。假如上一个有用的 \(v\) 为 \(v_1\)，对于某个 \(u < v_1 < v_2\)，假如 \(a_u < a_{v_2} < a_{v_1}\)，那么 \(v_2\) 可能为答案当且仅当 \(a_{v_2} - a_u < a_{v_1} - a_{v_2}\)。这意味着 \(a_{v_2} - a_u < \frac{1}{2}(a_u - a_{v_1})\)。那么我们发现，每出现一个有用的 \(v\) 都会使值域减半，那么合法的 \(v\) 就只有 \(O(\log n)\) 个。
那么我们就只需要对这 \(O(\log n)\) 个点对计算最小值即可。剩下的扫描线容易解决。
CodeChef MINXORSEG
给定一个序列 \(a_1, a_2, \cdots, a_n\)，每次询问一个区间 \([L, R]\)，求 \(u, v \in [L, R], u \ne v, a_u \oplus a_v\) 的最小值。
\(n, m \le 2 \times 10^5, a_i \le 10^9\)
类似的套路，对于某个 \(u\)，考虑有多少有用的 \(v\)。假如对于三个数 \(u < v_1 < v_2\)，先去掉 \(a_u, a_{v_1}, a_{v_2}\) 的 LCP，考虑剩下的开头。
首先开头不可能都相等，那么假如 \(a_{v_1}, a_{v_2}\) 的高位相同，那么选取 \(v_1, v_2\) 要比选择 \(u, v_2\) 更优；
若 \(a_u, a_{v_1}\) 高位相同，那么选取 \(u, v_1\) 比选取 \(u, v_2\) 更优；
所以，只有 \(a_u, a_{v_2}\) 高位相等时才有用。而此时 \(u, v_2\) 高位相等，LCP 就会再去一位（若不能去显然更劣），而这样 LCP 一共只会去 \(O(\log V)\) 次，所以一共就有 \(O(n \log V)\) 对支配对。
P9058 [Ynoi2004] rpmtdq
给你一棵 \(n\) 个点的树，边权为正数。定义 \(\mathrm{dist}(u, v)\) 为树上 \(u \to v\) 的最短路径长。
有 \(m\) 次询问，每次给定 \([l, r]\)，对于所有的 \(l \le u < v \le r\)，求 \(\min\{\mathrm{dist}(u, v)\}\)。
\(n \le 2 \times 10^5, m \le 10^6\)
这种存在两维信息的问题一般选取较复杂的一维进行分治。
考虑对树进行边分治。对于一条边，考虑经过这条边的所有路径。
首先，我们有一个朴素的想法：求出每个点到边的距离，对于每一个点，选取另一边的距离前驱和后继。但是，这样只能保证距离最小，但是不能保证它为支配对，当区间缩小时可能会有距离更大但是没有统计的点对。
考虑对距离进行限制，再求编号的前驱与后继。假如树的左边有一个点 \(u\)，右方有两个点 \(v_1, v_2\)，\(u < v_1 < v_2\)。那么假如 \(u, v_2\) 更优肯定需要有 \(\mathrm{dist(u, v_1)} \le \mathrm{dist}(v_1, v_2)\)。那么假如 \(u\) 距离中心的距离为 \(a\)，我们只考虑右边距离中心的距离 \(\le a\) 的点，那么我们就发现一定有 \(\mathrm{dist(u, v_1)} > \mathrm{dist}(v_1, v_2)\)。
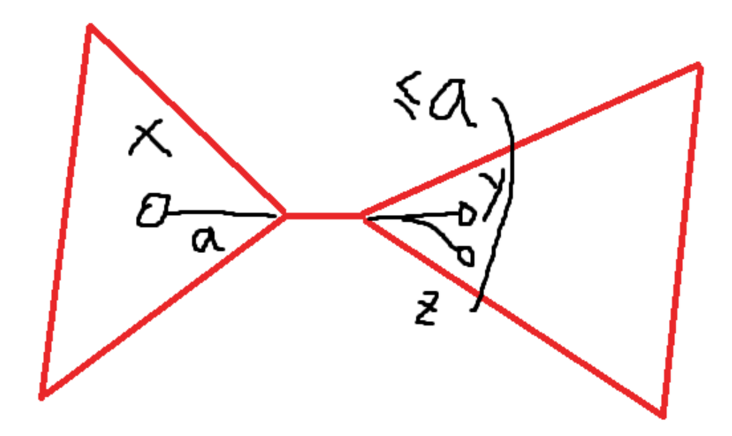
这意味着，只有前驱后继是有用的了。而我们发现，对距离进行这样的限制是可以考虑到所有点对的，因为每对点中必定有一个距离更远，距离更远的那个点就可以统计到这个点对。
所以每次所有点都只有 \(O(1)\) 个支配对，而树分治中共有 \(O(n \log n)\) 个点，所以总支配对还是 \(O(n \log n)\) 的。
最后同样再上扫描线就做完了。
杂题
没听，吃饭去了。
