「解题报告」P7163 [COCI2020-2021#2] Svjetlo

模拟赛出了这题，考场上我想了一种另类换根 DP 做法，赛时没调出来 \(O(n)\) 的做法，赛后调了调调出来了，发现做法与题解都不一样，虽然我的做法相对麻烦的多吧。

题目传送门

题目大意

给定一棵树，每个点有点亮与未点亮两种状态。现在从选中的一个点开始，每次走到相邻的节点，每经过一个节点都会使节点的状态翻转。
求将所有点都点亮的最短路径长度。
\(n \le 5\times 10^5\)

思路

首先可以想到 树形 DP。从任意一个起点开始感觉不太好 DP，那么我们就先钦定以根节点为起始点，求出这样的最短路径长度。

我们考虑一个路径大概长什么样子：

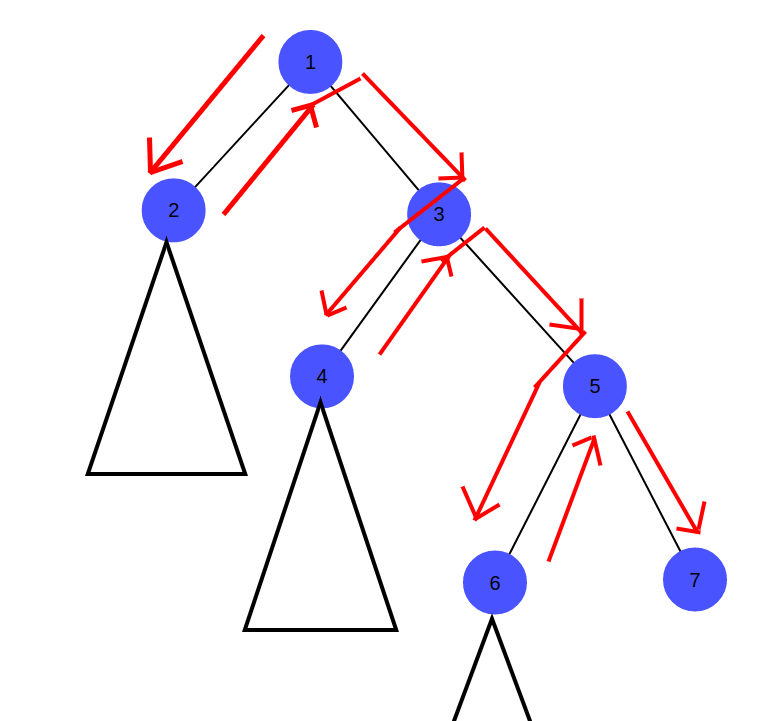
发现会有两种情况：一种是从一个子树的根节点出发，将子树中所有节点点亮后回到根节点；另一种是将所有子树点亮后，往一个子树内走。

我们可以根据这样的过程定义状态：

（注：以下根节点指当前节点 \(u\)）

设 \(f_{u,0}\) 为将一个子树内的所有节点全部点亮（不考虑根节点），所需要的最短路径长度。

如果一个根节点是亮的那就不用管了，但是如果走完所有子树后根节点没亮呢？

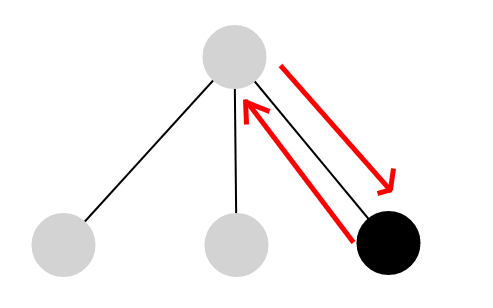
我们可以考虑在它的父亲节点时，只需要走完所有子树后，再往这个没亮的节点走一次，走回来就可以使这个儿子节点点亮。

具体的，对于一个转移，我们先跳到子树里，从子树里走，然后跳一步跳回根节点，最后看如果那个节点没有亮，就往下走一步再走回来把它点亮。

同时我们发现，这样做完操作之后，根节点的颜色一定是固定的（因为只有一种决策方式），那么我们可以记录下来这个颜色，设它为 \(f_{u,1}\)。

那么大致转移就是：

\[f_{u,0}=1+\sum_{v\in son_u}f_{v,0} + 2 \times [f_{v,1}=1] \]

\[f_{u,1}=1 \oplus s_u \oplus \bigoplus_{v\in son_u} f_{v,1} \]

（\(s_u\) 为 \(u\) 节点的初始状态，两个转移式子都有 \(1\) 的原因是要考虑刚进入根节点时造成的那一次贡献）

第二种情况就是我们从一个根节点走完其它子树后直接往下走，那么我们肯定是先把一些子树全部走完，然后选择一颗子树往下递归下去。那么发现根据选择的子树不同，走完后根节点的颜色也是不同的。所以我们设 \(f_{u,2}\) 为根节点不亮的情况，\(f_{u,3}\) 为根节点亮的情况。

若根节点未点亮，和上面的处理方法是相同的，考虑在它的父节点处走下去再走上来将它点亮。所以若转移到 \(f_{u,2}\)，那么根节点的颜色会翻转。

所以转移大概是：

\[f_{u,2+[f_{u,1} \oplus f_{v,1} \oplus 1]} = \min_{v\in son_u} \{f_{u,0} - (f_{v,0} + 2 \times [f_{v,1}=1]) + f_{v,2} + 2\} \]

\[f_{u,2+[f_{u,1} \oplus f_{v,1}]} = \min_{v\in son_u} \{f_{u,0} - (f_{v,0} + 2 \times [f_{v,1}=1]) + f_{v,3}\} \]

（即将 \(v\) 回到根节点的贡献去掉之后改为直接向下走的贡献）

注意我们也可指直接走完整颗子树然后回到根节点，不再往下走，所以我们要设初值：

\[f_{u, 2 + f_{u, 1}}=f_{u, 0} \]

需要注意的是，如果整个子树都是点亮状态，我们分两种情况：根节点也点亮了和根节点未点亮。直接特殊处理出来这两种情况的 DP 值就可以了。

单次 DP 代码：

void update(int u, int pre) {
    f[u][0] = -1;
    int sum = 0, col = s[u];
    for (int v : e[u]) if (v != pre) { 
        if (f[v][0] != -1) f[u][0] = 1;
        sum += f[v][0] + 2 * (f[v][1] == 0) + 1;
        col ^= f[v][1] ^ (f[v][0] == -1);
    }
    if (col == 1 && f[u][0] == -1) {
        f[u][0] = -1;
        f[u][1] = 1;
        f[u][2] = 0x3f3f3f3f;
        f[u][3] = 0;
    } else if (col == 0 && f[u][0] == -1) {
        f[u][0] = 1;
        f[u][1] = 1;
        f[u][2] = 0x3f3f3f3f;
        f[u][3] = 1;
    } else {
        col ^= 1;
        f[u][0] = 1 + sum;
        f[u][1] = col;
        f[u][2] = f[u][3] = 0x3f3f3f3f;
        f[u][2 + col] = min(f[u][2 + col], f[u][0]);
        for (int v : e[u]) if (v != pre) {
            f[u][2 + (col ^ f[v][1] ^ 1)] = min(f[u][2 + (col ^ f[v][1] ^ 1)], 
                f[u][0] - (f[v][0] + 2 * (f[v][1] == 0) + 1) + f[v][2] + 2);
            f[u][2 + (col ^ f[v][1])] = min(f[u][2 + (col ^ f[v][1])], 
                f[u][0] - (f[v][0] + 2 * (f[v][1] == 0) + 1) + f[v][3]);
        }
    }
}

接下来考虑换根。

\(f_{u,0}\) 和 \(f_{u,1}\) 是容易的，因为他们都是和的形式和异或和的形式，不过需要注意都点亮的情况，因为换根后原来都点亮的子树可能不再都点亮。

所以我们可以维护三个数组 \(psum_u,pcol_u,pcnt_u\)，分别表示 \(u\) 节点在没有全部点亮的情况下得到的 \(f_{u,0},f_{u,1}\) 值和有多少个子树没有被点亮。

这样我们在转移的时候就可以轻松处理子树全部点亮的情况了。具体的，当 \(pcnt_u=0\) 时，就说明子树全部被点亮了。

对于 \(f_{u,2},f_{u,3}\)，它们的转移是 \(O(size_u)\) 的，直接换根显然可以被卡到 \(O(n^2)\)（构造菊花图）。但是观察 DP 的形式：\(f_{u,0}\) 是只跟当前节点的 DP 值有关系的，而剩下的加起来只跟 \(v\) 有关系。所以我们发现，对于每一个 \(u\)，只有 \(2\) 个 \(v\) 是可能造成贡献的。 因为如果最小值的那个子树在换根的时候删除了，那么就肯定会轮到第二小的子树造成贡献，更大的值是肯定不会造成贡献的。同时考虑当前节点的根节点可能已经被更改过，所以要把当前节点的父亲节点加进去。

于是我们跑第一遍 DP 的时候可以处理出每个节点可能的 \(5\) 个决策点（两个 DP 式子各 \(2\) 个，再加上一个父亲节点共 \(5\) 个），然后再换根的时候只遍历这几个子树就可以了。

于是我们就做到了复杂度 \(O(n)\) 解决该问题。

~~代码非常好写，你信我~~

代码

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 500005;
vector<int> e[MAXN], e2[MAXN]; // e2: 可能的决策点
int n;
char s[MAXN];
int f[MAXN][4];
int psum[MAXN], pcol[MAXN], pcnt[MAXN];
void remove(int u, int pre) { // 从当前子树中删除 pre 节点
    int &sum = psum[u], &col = pcol[u];
    if (f[pre][0] != -1) pcnt[u]--;
    sum -= f[pre][0] + 2 * (f[pre][1] == 0) + 1;
    col ^= f[pre][1] ^ (f[pre][0] == -1);
    if (pcnt[u] == 0) {
        f[u][0] = -1;
    } else {
        f[u][0] = 1;
    }
    if (col == 1 && f[u][0] == -1) {
        f[u][0] = -1;
        f[u][1] = 1;
        f[u][2] = 0x3f3f3f3f;
        f[u][3] = 0;
    } else if (col == 0 && f[u][0] == -1) {
        f[u][0] = 1;
        f[u][1] = 1;
        f[u][2] = 0x3f3f3f3f;
        f[u][3] = 1;
    } else {
        f[u][0] = 1 + sum;
        f[u][1] = (col ^ 1);
        f[u][2] = f[u][3] = 0x3f3f3f3f;
        f[u][2 + (col ^ 1)] = min(f[u][2 + (col ^ 1)], f[u][0]);
        for (int v : e2[u]) if (v != pre) { // 注意排除要删掉的节点
            f[u][2 + ((col ^ 1) ^ f[v][1] ^ 1)] = min(f[u][2 + ((col ^ 1) ^ f[v][1] ^ 1)], 
                f[u][0] - (f[v][0] + 2 * (f[v][1] == 0) + 1) + f[v][2] + 2);
            f[u][2 + ((col ^ 1) ^ f[v][1])] = min(f[u][2 + ((col ^ 1) ^ f[v][1])], 
                f[u][0] - (f[v][0] + 2 * (f[v][1] == 0) + 1) + f[v][3]);
        }
    }
}
void add(int u, int pre) { // 从当前子树添加 pre 节点
    int &sum = psum[u], &col = pcol[u];
    if (f[pre][0] != -1) pcnt[u]++;
    sum += f[pre][0] + 2 * (f[pre][1] == 0) + 1;
    col ^= f[pre][1] ^ (f[pre][0] == -1);
    if (pcnt[u] == 0) {
        f[u][0] = -1;
    } else {
        f[u][0] = 1;
    }
    if (col == 1 && f[u][0] == -1) {
        f[u][0] = -1;
        f[u][1] = 1;
        f[u][2] = 0x3f3f3f3f;
        f[u][3] = 0;
    } else if (col == 0 && f[u][0] == -1) {
        f[u][0] = 1;
        f[u][1] = 1;
        f[u][2] = 0x3f3f3f3f;
        f[u][3] = 1;
    } else {
        f[u][0] = 1 + sum;
        f[u][1] = (col ^ 1);
        f[u][2] = f[u][3] = 0x3f3f3f3f;
        f[u][2 + (col ^ 1)] = min(f[u][2 + (col ^ 1)], f[u][0]);
        for (int v : e2[u]) {
            f[u][2 + ((col ^ 1) ^ f[v][1] ^ 1)] = min(f[u][2 + ((col ^ 1) ^ f[v][1] ^ 1)], 
                f[u][0] - (f[v][0] + 2 * (f[v][1] == 0) + 1) + f[v][2] + 2);
            f[u][2 + ((col ^ 1) ^ f[v][1])] = min(f[u][2 + ((col ^ 1) ^ f[v][1])], 
                f[u][0] - (f[v][0] + 2 * (f[v][1] == 0) + 1) + f[v][3]);
        }
    }
}
void dfs(int u, int pre) {
    for (int v : e[u]) if (v != pre) {
        dfs(v, u);
    }
    f[u][0] = -1;
    int sum = 0, col = s[u];
    for (int v : e[u]) if (v != pre) { 
        if (f[v][0] != -1) f[u][0] = 1;
        sum += f[v][0] + 2 * (f[v][1] == 0) + 1;
        col ^= f[v][1] ^ (f[v][0] == -1);
    }
    if (col == 1 && f[u][0] == -1) {
        f[u][0] = -1;
        f[u][1] = 1;
        f[u][2] = 0x3f3f3f3f;
        f[u][3] = 0;
        e2[u].push_back(pre);
    } else if (col == 0 && f[u][0] == -1) {
        f[u][0] = 1;
        f[u][1] = 1;
        f[u][2] = 0x3f3f3f3f;
        f[u][3] = 1;
        e2[u].push_back(pre);
    } else {
        col ^= 1;
        f[u][0] = 1 + sum;
        f[u][1] = col;
        f[u][2] = f[u][3] = 0x3f3f3f3f;
        f[u][2 + col] = min(f[u][2 + col], f[u][0]);
        queue<int> q[2];
        for (int v : e[u]) if (v != pre) {
            if (f[u][2 + (col ^ f[v][1] ^ 1)] >= 
                f[u][0] - (f[v][0] + 2 * (f[v][1] == 0) + 1) + f[v][2] + 2) {
                    q[(col ^ f[v][1] ^ 1)].push(v);
                    if (q[(col ^ f[v][1] ^ 1)].size() > 2) q[(col ^ f[v][1] ^ 1)].pop();
                }
            if (f[u][2 + (col ^ f[v][1])] >=
                f[u][0] - (f[v][0] + 2 * (f[v][1] == 0) + 1) + f[v][3]) {
                    q[(col ^ f[v][1])].push(v);
                    if (q[(col ^ f[v][1])].size() > 2) q[(col ^ f[v][1])].pop();
                }
            f[u][2 + (col ^ f[v][1] ^ 1)] = min(f[u][2 + (col ^ f[v][1] ^ 1)], 
                f[u][0] - (f[v][0] + 2 * (f[v][1] == 0) + 1) + f[v][2] + 2);
            f[u][2 + (col ^ f[v][1])] = min(f[u][2 + (col ^ f[v][1])], 
                f[u][0] - (f[v][0] + 2 * (f[v][1] == 0) + 1) + f[v][3]);
        }
        while (!q[0].empty()) e2[u].push_back(q[0].front()), q[0].pop();
        while (!q[1].empty()) e2[u].push_back(q[1].front()), q[1].pop();
        if (pre) e2[u].push_back(pre);
    }
    pcol[u] = s[u];
    for (int v : e[u]) if (v != pre) { 
        if (f[v][0] != -1) pcnt[u]++;
        psum[u] += f[v][0] + 2 * (f[v][1] == 0) + 1;
        pcol[u] ^= f[v][1] ^ (f[v][0] == -1);
    }
}
void changeRoot(int u, int v) {
    remove(u, v);
    add(v, u);
}
int ans = INT_MAX;
void dfs2(int u, int pre) { // 换根 DP
    ans = min(ans, f[u][3]);
    for (int v : e[u]) if (v != pre) {
        changeRoot(u, v);
        dfs2(v, u);
        changeRoot(v, u);
    }
}
int main() {
    scanf("%d%s", &n, s + 1);
    for (int i = 1; i <= n; i++) s[i] ^= '0';
    for (int i = 1; i < n; i++) {
        int x, y; scanf("%d%d", &x, &y);
        e[x].push_back(y);
        e[y].push_back(x);
    }
    memset(f, 0x3f, sizeof f);
    dfs(1, 0);
    dfs2(1, 0);
    printf("%d\n", ans);
    return 0;
}

posted @ 2022-08-05 20:26 APJifengc 阅读(65) 评论(0) 编辑收藏举报

刷新页面返回顶部

apjifengc's blog

「解题报告」P7163 [COCI2020-2021#2] Svjetlo

题目大意

思路

代码