动态规划—硬币收集问题

例3《硬币收集问题》

问题描述:

在N x M格木板中放有一些硬币，每格的硬币数目最多为一个。在木板左上方的一个机器人需要收集尽可能多的硬币并把它们带到右下方的单元格。每一步，机器人可以从当前的位置向右移动一格或向下移动一格。当机器人遇到一个有硬币的单元格时，就会将这枚硬币收集起来。设计一个算法找出机器人能找到的最大硬币数。

分析：

1.令F（i，j）为机器人截止到第i行第j列单元格（i，j）能够收集到的最大硬币数。单元格（i，j）可以经由上方相邻单元格（i-1，j）或者左边相邻单元格（i，j-1）到达。单元格（i-1，j）和单元格（i，j-1）中最大的硬币数目分别是F（i-1，j）和F（i，j-1）。当然，第一行单元格没有上方相邻单元格，第一列单元格没有左边相邻单元格。对这些单元格，我们假定F（i-1，j）或F（i，j-1）的值为0，因为其不存在相应的相邻单元格。因此，截止到单元格（i，j）机器人能够收集到的最大硬币数是这两个数的较大值加上单元格（i，j）中可能存在的一枚硬币。

2.递推公式为：

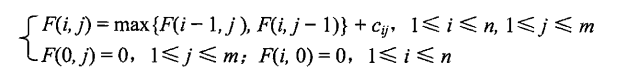
代码:

package algorithm;
public class demo_1 {
    //输出找到最大硬币数的路径
    public void getMaxPath(int[][] A){
        int rowA = A.length;
        int columnA = A[0].length;         
        //在数组A最上面一行添加一行元素0，在最左边一列添加一列元素0
        int[][] changeA = new int[rowA+1][columnA+1];  //初始化，各个元素均为0
        int[][] maxA = new int[rowA+1][columnA+1];   //用于计算从A[0][0]到达各元素位置收集到的最大硬币数
        for(int i = 0;i < rowA;i++){
            for(int j = 0;j < columnA;j++)
                changeA[i+1][j+1] = A[i][j];
        }
        for(int i = 1;i <= rowA;i++){
            for(int j = 1; j <= columnA;j++){
                if(maxA[i-1][j] >= maxA[i][j-1])
                    maxA[i][j] = maxA[i-1][j] + changeA[i][j];
                else
                    maxA[i][j] = maxA[i][j-1] + changeA[i][j];
            }
        }
        
        //输出各个元素位置收集到的最大硬币数
        System.out.println("各个元素位置收集到的最大硬币数：");
        for(int i = 1;i <= rowA;i++){
            for(int j = 1;j <= columnA;j++)
                System.out.print(maxA[i][j]+"\t");
            System.out.println();
        }   
    }
  
    public static void main(String[] args){
        demo_1 test = new demo_1();
        int[][] A ={{0,0,0,0,1,0},
                {0,1,0,1,0,0},
                {0,0,0,1,0,1},
                {0,0,1,0,0,1},
                {1,0,0,0,1,0}};
        test.getMaxPath(A);
    }
}

3.测试数据：

int[][] A ={{0,0,0,0,1,0},
{0,1,0,1,0,0},
{0,0,0,1,0,1},
{0,0,1,0,0,1},
{1,0,0,0,1,0}};

结果：

各个元素位置收集到的最大硬币数：
0 0 0 0 1 1
0 1 1 2 2 2
0 1 1 3 3 4
0 1 2 3 3 5
1 1 2 3 4 5