41. First Missing Positive
Given an unsorted integer array, find the first missing positive integer.
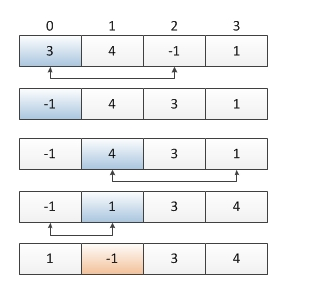
For example,Given [1,2,0] return 3,and [3,4,-1,1] return 2.Your algorithm should run in O(n) time and uses constant space.Naive的方法肯定是sort这个数组,但那样要用O(NlongN)的时间;第二种思路是用哈希表映射,Mapping all positive integers to a hash table and iterate from 1 to the length of the array to find out the first missing one,但哈希表是O(N)的space. 那怎么做呢?
Li Shi's Analysis:
The idea is to use the array itself as a table. We try put a value i on the place i-1. If the value i is out of range, i.e., <=0 || >n, then ignore it. At each position i, we check whether the A[i] is a value needed to be placed on its own position, if yes, we swap it; then we check the new A[i] again. We repeat this procedure until A[i] is a value that is out of range or the right place of value A[i] is already placed a value of A[i] (Duplicate situation), we then move the i+1 position.
不能开辟非常数的额外空间,就需要在原数组上操作,思路是交换数组元素,让数组中index为i的位置存放数值(i+1)。最后如果哪个数组元素违反了A[i]=i+1即说明i+1就是我们要求的第一个缺失的正数。具体操作如下:
- if A[i] is positive, say we have A[i] = x, we know it should be in slot A[x-1]! That is to say, we can swap A[x-1] with A[i] so as to place x into the right place.
- if A[i] is non-positive, 0, or A[i]>A.length, ignore it;
- if A[i] == A[A[i]-1], we do not swap, two cases, 1. Maybe A[i] = i+1, A[i]is correct; 2. though A[i] is not correct like [1, 1] index 1, but A[0] == A[1], swap A[1] with A[0] will only give rise to infinite loop
public class Solution {
public int firstMissingPositive(int[] A) {
if (A==null && A.length==0) {
return 1;
}
for (int i=0; i<A.length; i++) {
if (A[i]>0 && A[i]<=A.length && A[i]!=A[A[i]-1]) {
int temp = A[A[i]-1];
A[A[i]-1] = A[i];
A[i] = temp;
i--;
}
}
for (int i=0; i<A.length; i++) {
if (A[i] != i+1) return i+1;
}
return A.length+1;
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号