Edit Distance

Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. 
(each operation is counted as 1 step.)

You have the following 3 operations permitted on a word:

a) Insert a character
b) Delete a character
c) Replace a character

Given word1 = "mart" and word2 = "karma", return 3.

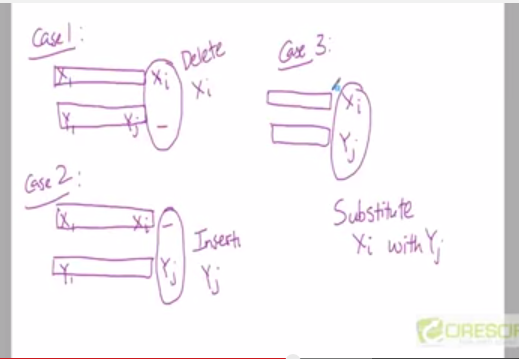
res[i][j]表示Edit Distance between X数组的前i个元素以及Y数组的前j个元素，或者the minimum # of operations to convert X前i个元素 into Y的前j个元素

因为对于Xi 和 Yj，操作无非是 insert, delete, replace三种，所以递归式就是三项：根据上面这个图很清楚：res[i][j] = min{res[i-1][j]+1, res[i][j-1]+1, Xi == Yj ? res[i-1][j-1] : res[i-1][j-1] + 1}

 

Use f[i][j] to represent the shortest edit distance between word1[0,i) and word2[0, j). Then compare the last character of word1[0,i) and word2[0,j), which are c and d respectively (c == word1[i-1], d == word2[j-1]):

if c == d, then : f[i][j] = f[i-1][j-1]

Otherwise we can use three operations to convert word1 to word2:

(a) if we replaced c with d: f[i][j] = f[i-1][j-1] + 1;

(b) if we added d after c: f[i][j] = f[i][j-1] + 1;

(c) if we deleted c: f[i][j] = f[i-1][j] + 1;

Note that f[i][j] only depends on f[i-1][j-1], f[i-1][j] and f[i][j-1], therefore we can reduce the space to O(n) by using only the (i-1)th array and previous updated element(f[i][j-1]).

public int minDistance(String word1, String word2) {
        // write your code here
        // state
        int m = word1.length(), n = word2.length();
        /*if (word1 == null || word2 == null || )*/
        int[][] f = new int[m + 1][n + 1];
        // initialize
        f[0][0] = 0;
        for (int i = 1; i <= m; i++) {
            f[i][0] = i;
        }
         for (int i = 1; i <= n; i++) {
            f[0][i] = i;
        }
        
        // function
         for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    f[i][j] = /*f[i - 1][j - 1]*/ Math.min(f[i - 1][j - 1], Math.min(f[i - 1][j] + 1, f[i][j - 1] + 1));
                } else {
                     f[i][j] = Math.min(f[i - 1][j - 1] + 1, Math.min(f[i - 1][j] + 1, f[i][j - 1] + 1));
                }
            }
        }
        return f[m][n];
    }

//Note that f[i][j] only depends on f[i-1][j-1], f[i-1][j] and f[i][j-1], therefore we can reduce the space to O(n) by using only the (i-1)th array and previous updated element(f[i][j-1]).

 

int minDistance(string word1, string word2) {
    
        int l1 = word1.size();
        int l2 = word2.size();
    
        
        int[] f = new int[l2 + 1];
        for (int j = 1; j <= l2; ++j)
            f[j] = j;
    
        for (int i = 1; i <= l1; ++i)
        {
            int prev = i;
            for (int j = 1; j <= l2; ++j)
            {
                int cur;
                if (word1[i-1] == word2[j-1]) {
                    cur = f[j-1];
                } else {
                    cur = min(min(f[j-1], prev), f[j]) + 1;
                }
    
                f[j-1] = prev;
                prev = cur;
            }
            f[l2] = prev;
        }
        return f[l2];
    
    }  

　　

写好状态后, 想想与上一个状态怎么用题意联系起来, 上一个状态常常是遍历的上一个状态, 字符串问题常常要考虑上一个字母是否匹配来分情况讨论