407. Trapping Rain Water II

Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.

Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.

Example:

Given the following 3x6 height map:
[
  [1,4,3,1,3,2],
  [3,2,1,3,2,4],
  [2,3,3,2,3,1]
]

Return 4.

 

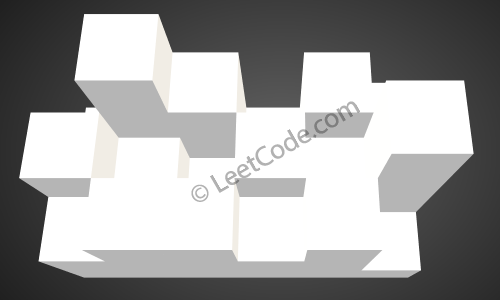
The above image represents the elevation map [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.

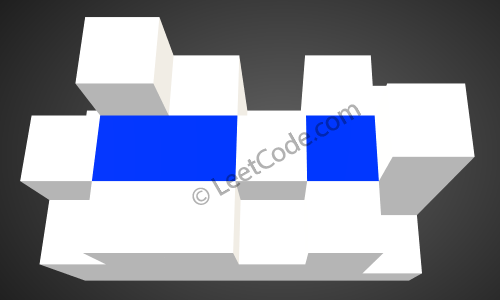
After the rain, water are trapped between the blocks. The total volume of water trapped is 4.

fb : 考过一

Analysis, 根据木桶原理，先找外围最矮的bar，里边如果有bar比它还矮，一定能存水（因为四周所有的bar都比它高）

注意还可能存更多的水，因为往里面，很可能cell高度变化。所以要把BFS中间遇到的高的bar都存进queue，随着水平面提升，提升到这些bar的高度，看能不能有凹槽存更多的水

44-45行逻辑就是

 if (height[row][col] < cur) {

　　res += cur.height- height[row][col];

　　queue.offer(new Cell(row, col, cur.height));

}

else {

　　queue.offer(new Cell(row, col, height[row][col]));

}

public class Solution {

    public class Cell {
        int row;
        int col;
        int height;
        public Cell(int row, int col, int height) {
            this.row = row;
            this.col = col;
            this.height = height;
        }
    }

    public int trapRainWater(int[][] heights) {
        if (heights == null || heights.length == 0 || heights[0].length == 0)
            return 0;
　　　　// 创建heap,时复写comparator, 因为里面的元素时cell, 需要明确compare方法比较的内容
        PriorityQueue<Cell> queue = new PriorityQueue<>(1, new Comparator<Cell>(){
            public int compare(Cell a, Cell b) {
                return a.height - b.height;
            }
        });
        
        int m = heights.length;
        int n = heights[0].length;
        boolean[][] visited = new boolean[m][n];

        // Initially, add all the Cells which are on borders to the queue.
        for (int i = 0; i < m; i++) {
            visited[i][0] = true;
            visited[i][n - 1] = true;
            queue.offer(new Cell(i, 0, heights[i][0]));
            queue.offer(new Cell(i, n - 1, heights[i][n - 1]));
        }

        for (int i = 0; i < n; i++) {
            visited[0][i] = true;
            visited[m - 1][i] = true;
            queue.offer(new Cell(0, i, heights[0][i]));
            queue.offer(new Cell(m - 1, i, heights[m - 1][i]));
        }

        // from the borders, pick the shortest cell visited and check its neighbors:
        // if the neighbor is shorter, collect the water it can trap and update its height as its height plus the water trapped
       // add all its neighbors to the queue.
        int[][] dirs = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        int res = 0;
        while (!queue.isEmpty()) {
            Cell cell = queue.poll();
            for (int[] dir : dirs) {
                int row = cell.row + dir[0];
                int col = cell.col + dir[1];
                if (row >= 0 && row < m && col >= 0 && col < n && !visited[row][col]) {
                    visited[row][col] = true;
                    res += Math.max(0, cell.height - heights[row][col]);
                    queue.offer(new Cell(row, col, Math.max(heights[row][col], cell.height)));
                }
            }
        }
        
        return res;
    }
}

　　这里是矩阵, 在构建图时不需要用map来存储键值对以达到遍历的目的, 但是需要有元素大小的比较, 因此用heap, 与

399. Evaluate Division 数据结构, 算法也不同, 一个是map 上的dfs, 一个是矩阵上的bfs, 一个是要找到一条自始至终的路径, 一个是遍历完所有相邻的点求值(根据题意)

但是bfs要点在于如何建图, 是否建类, 建比较器, 建方向容器, 建走过的路的存储器(数组, 或者set, list) 如何遍历(堆不空?), 遍历到内部的点时判断是否符合题意(边界, 走过), 再考虑题意, 判断当前的点是否符合题意来加入结果的容器 或结果值, 将当前的点加入堆中是否要改变值啊什么的, 关键在于建立的是什么图. 里面的点是怎么个意思, 都是题意的转化