算法题解----分解质因数 + 筛质数的三种算法

第一部分 ： 分解质因数

任何一个大于 1 的正整数都可以写成这样的形式：

　　

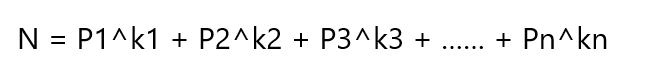
其中 Pi 是 一个质数

那么我们可以用怎么样的算法去得到 这个正整数的 质因数以及其 指数呢？

我们可以用 试除法这个方法：
① 找到N的一个 质约数 然后让N一只除这个质约数，直到 N % Pi != 0 

② 记录我们除这个质约数除了多少次 那么次数就是这个质约数的指数

这里还有几点要注意：

我们循环控制变量i 是这样循环的 for( i = 2 ; i <= n/i ; i++)

这样就可以找到N的绝大部分质因数 不过有可能我们会漏掉一个质因数

比如说当N很大的时候 他可能有一个质因数是大于 sqrt(N) 的

所以我们最后要进行一个判断 if( N>1 ) 那么最后N就是原来N的最后一个最大的质因数 而且这个质因数的指数一定是1

 

话不多说，上代码~

 

 

int cnt,primes[N];                            //存储质因数
int s[N];                                     //存储指数    

void divide(int n)
{
    for(int i = 2 ; i <= n / i ; i ++)
    {
         if(n % i == 0)
         {   
               primes[cnt++] = i;
               while( n%i == 0 )
             {
                 s[cnt]++;
                 n /= i;
             }
    }
    
      if(n>1)
     {
         primes[cnt] = n;
         s[cnt] = 1; 
     }
}    

 

 

 

 第二部分：筛质数

学过编程的同学一定都写过筛质数的程序吧

很经典的一道题 ： 筛取1000以内的质数

里面有一种比较好的算法：

 

bool is_prime(int n)
{
    for(int i=2 ; i<=n/i;i++)
    {
          if(n % i ==0)
          {
                return false;
           } 
    }
    return true;
}    

 

这就是试除法筛素数的算法，那么为什么我们要设置 i <= n/i 而不是 i <= n-1 呢 ？

因为我们这个算法是用来判断这个数是不是素数，如果这个数是合数那个它一定可以写成 a * b 且 a !=1 b != 1的形式 这是完全对称的，所以只用判断i到 sqrt(n)就可以了 。这个算法的时间复杂度为O(n logn)

那么对于筛素数我们有没有更高效的算法呢？

这里我就介绍两种筛素数的算法： 埃氏筛和线性筛

首先介绍埃氏筛：

 

我们还要用一个st数组来存储每个数的状态，如果这个数被筛掉了就把这个st设置为true

话不多说 上代码

int cnt,primes[N];
bool st[N];
void get_primes(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(!st[i])                    //如果i是质数
        {
             primes[cnt++] = i;
             for(int j = i ; j <=n ;j+=i) st[j]=true;   //筛去i的倍数
         }
    }  

}

 

埃氏筛的算法时间复杂度为O（n loglogn） 是十分接近O(n)的时间复杂度的， 也是算法竞赛常用的筛质数的算法

为什么埃氏筛的时间复杂度不是O(n)的呢？

因为 如果用埃氏筛的算法 一个数可能要被筛掉很多次 。

我再来介绍一个更好的算法去筛质数：线性筛，从名字来看就知道线性筛的时间复杂度是O(n)的，那么线性筛是如何筛掉合数的呢？

其实线性筛的本质也是筛掉质数的倍数，不过它中间的过程和埃氏筛有点不同

埃氏筛是只要是质数是当前合数的质因子就筛

而线性筛思路是这样的，如果质因数是当前数的最小质因子，那么这个质因数也一定是这个质因数乘以当前数的最小质因子，那么就可以筛掉

避免了一个数被重复筛去的情况，好，那么代码是如何写的呢？

void get_primes(int n)
{
     for(int i=2 ;i<=n;i++)
     {
         if(!st[i]) primes[cnt++] = i;
         for(int j = 0; primes[j] <= n/i;j++)
         {
               st[primes[j] * i] = true;
               if(i % primes[j] == 0) break;
          }     
     }    
}